Inhaltsverzeichnis

1 Whiteboard zur Sitzung am 19. Juni
2 Verschiebungen
3 Schubspiegelungen
- 3.1 Definition
- 3.2 Die Definition ist keine Einschränkung

Whiteboard zur Sitzung am 19. Juni

Verschiebungen

Schubspiegelungen

Definition

Eine Schubspiegelung ist die Nacheinenderausführung einer Verschiebung mit einer Geradenspiegelung, wobei Verschiebungsrichtung und Spiegelachse parallel sind. Eine kleine Spielerei mit PovRay aus dem Jahr 1998. Das Ding das da verschoben und gespiegelt wird ist eine sogenannte Kleinsche Flasche

(https://de.wikipedia.org/wiki/Kleinsc...)

[ www.youtube.com is not an authorized iframe site ]

Die Definition ist keine Einschränkung

Ich habe ein altes Video wieder entdeckt. Es wurde 1998 mit PovRay (http://www.povray.org/) generiert. Das Rendern lief auf einem 486ger und hat wegen der eingebauten Spiegeleffekte eine ganze Nacht gedauert.

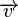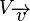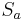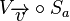Definition: Wenn der Verschiebungsvektor $\overrightarrow{v}$ einer Verschiebung $V_{\overrightarrow{v}}$ parallel zur Spiegelgeraden $a$ einer Spiegelung $S_a$ ist, dann ist die NAF $V_{\overrightarrow{v}} \circ S_a$ eine Schubspiegelung. Auf den ersten Blick meint man, dass die diese Definition eine Einschränkung des Begriffs Schubspiegelung ist. Das Video zeigt, dass dem nicht so ist. 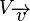Die Verschiebung $V_{\overrightarrow{v}}$ wird durch die NAF zweier Geradenspiegelungen ersetzt. Die beiden Spiegelachsen sind dabei parallel zueinander. 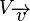$V_{\overrightarrow{v}}$ ist beliebig, d.h. die beiden Spiegelachsen, die letztlich die Verschiebung repräsentieren, stehen nicht senkrecht aufeinander. Insgesamt haben wir es mit der NAF von drei Geradenspiegelungen zu tun. Da die NAF beliebiger Abbildungen immer assoziativ ist, kann beliebig geklammert werden. Zunächst gehören die beiden parallelen Geraden zusammen (Verschiebung). Wir fassen die zweite Geradenspiegelung der Verschiebung mit der abschließenden Geradenspiegelung zusammen. Zusammen ergibt diese Kopplung eine Drehung. Diese Drehung wird äquivalent durch andere Geradenspiegelungen ersetzt. .... Am Ende der verschiedenen Zusammenfassungen und Ersetzungen erhalten wir zwei zueinender parallele Spiegelgeraden, die senkrecht auf einer dritten Spiegelgeraden stehen, also wieder die NAF einer Verschiebung mit einer Geradenspiegelung. Die Konstellation ist jetzt aber so, wie in der Definition zugelassen.