Das WB als SVG

Hinweis: Aus Zeitgründen stelle ich nur noch Kopien vom Whiteboard als Vektorgrafik ins Wiki. Vektorgrafiken sind verlustfrei. Sie können sie mittels Inkscape in die verschiedensten Formate (Postscript, PDF, PNG) umwandeln. Inkscape ist Freeware.

Kurze Zusammenfassung vorab

Jede Gerade, die nicht senkrecht auf der x-Achse steht lässt sich durch eine Gleichung der Form 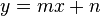$y=mx+n$ beschreiben.
$m$ ist der sogenannte Anstieg und lässt sich über Anstiegsdreiecke berechnen.
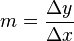
$m=\frac{\Delta y}{\Delta x}$
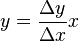
Geht die Gerade durch den Ursprung lautet ihre Gleichung $y=\frac{\Delta y}{\Delta x} x$
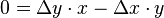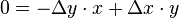
Die Gleichung geht über in $0=\Delta y\cdot x - \Delta x \cdot y$ oder $0=-\Delta y\cdot x + \Delta x \cdot y$
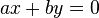
allgemein: $ax+by=0$
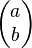$\begin{pmatrix} a \\ b\end{pmatrix}$ ist ein sogenannte Normalenvektor bzgl. der beschriebenen Geraden. Er Steht senkrecht auf der Geraden
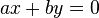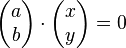Die Gleichung $ax+by=0$ lässt sich als Skalarprodukt interpretieren $\begin{pmatrix} a \\ b \end{pmatrix} \cdot \begin{pmatrix} x \\ y \end{pmatrix}=0$ .
Dieses Skalarprodukt lässt sich als Normalenvektor mal Ortsvektor eines Punkte auf der Geraden interpretieren.
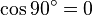
Ist der Punkt auf der Geraden verschwindet das Skalarprodukt, denn Ortsvektor und Normalenvektor stehen senkrecht aufeinander: $\cos 90^\circ =0$
Ist der Punkt nicht auf der Geraden verschwindet das Skalarprodukt nicht und die Gleichung 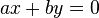$ax+by=0$ ist nicht erfüllt.