Der Mittelpunkt einer Strecke
Wir wissen nun, dass eine offene Strecke  die Menge aller Punkte ist, die zwischen die Menge aller Punkte ist, die zwischen  und und  liegen. Vereinigt man diese Menge mit der Menge der beiden Endpunkte liegen. Vereinigt man diese Menge mit der Menge der beiden Endpunkte  und und  , so hat man die gesamte Strecke , so hat man die gesamte Strecke  . Zu unseren grundlegenden Vorstellungen von Strecken gehört, dass jede Strecke . Zu unseren grundlegenden Vorstellungen von Strecken gehört, dass jede Strecke  einen Mittelpunkt einen Mittelpunkt  hat. hat.  wäre der Punkt auf wäre der Punkt auf  , der sowohl zu , der sowohl zu  als auch zu als auch zu  denselben Abstand denselben Abstand 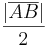 hat. hat.
Definition III.1: (Mittelpunkt einer Strecke)
Satz III.1: (Existenz und Eindeutigkeit des Mittelpunkte einer Strecke)
- Jede Strecke hat genau einen Mittelpunkt.
Beweis der Existenz und Eindeutigkeit des Mittelpunktes einer Strecke
- Die Materie erscheint einsichtig und einfach. Übungsaufgabe?? Nichts ist einfach. Mit den bisher bereitgestellten axiomatischen Grundlagen unserer Geometrie wird es Ihnen nicht gelingen, etwa zu zeigen, dass jede Strecke einen Mittelpunkt besitzt.
Der Knackpunkt bezüglich des Nachweises der Existenz und Eindeutigkeit des Streckenmittelpunktes besteht darin, dass unsere derzeitige Theorie noch nicht genügend Punkte zu Verfügung stellt. Momentan muss unser Raum nicht mehr als 4 Punkte enthalten. Nach Axiom I.7 sind diese vier Punkte nicht komplanar, woraus folgt, dass je drei von ihnen nicht auf ein und derselben Geraden liegen. Damit könnte eine durch zwei verschiedene dieser vier Punkte eindeutig bestimmte Strecke gar keinen Mittelpunkt haben, denn dieser müsste entsprechend Definition III.1 bezüglich unserer zwei Endpunkte auf derselben Geraden liegen.
Es wird Zeit, die Anzahl Punkte unserer Theorie radikal zu erhöhen. Konzentrieren wir uns diesbezüglich zunächst auf einen Strahl  . Nach unserer Vorstellung von Halbgeraden können wir je zwei Punkten von . Nach unserer Vorstellung von Halbgeraden können wir je zwei Punkten von  genau eine nichtnegative reelle Zahl (den Abstand der beiden Punkte) zuordnen. Nach unseren Vorstellungen etwa von Zahlenstrahl gibt es auch zu jeder nicht negativen reellen Zahl d genau einen Punkt genau eine nichtnegative reelle Zahl (den Abstand der beiden Punkte) zuordnen. Nach unseren Vorstellungen etwa von Zahlenstrahl gibt es auch zu jeder nicht negativen reellen Zahl d genau einen Punkt 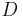 auf auf  , der zu , der zu  gerade den Abstand gerade den Abstand 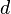 hat. Bei Konstruktionsaufgaben finden wir diese Idee im Zusammenhang mit dem Streckenantragen wieder. hat. Bei Konstruktionsaufgaben finden wir diese Idee im Zusammenhang mit dem Streckenantragen wieder.
Streckenantragen
Das Axiom vom Lineal
Wir sind überzeugt davon, dass unsere Konstruktion entsprechend des vorangegangenen Abschnitts immer funktioniert und der so gewonnene zweite Endpunkt unserer konstruierten Strecke eindeutig bestimmt ist. Die Idee des Streckenantragens müssen wir jetzt jedoch axiomatisch fordern bzw. begründen.
Axiom III.1: (Axiom vom Lineal)
- Zu jeder nicht negativen reelen Zahl
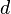 gibt es auf jedem Strahl gibt es auf jedem Strahl  genau einen Punkt, der zum Anfangspunkt von genau einen Punkt, der zum Anfangspunkt von  den Abstand den Abstand 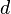 hat. hat.
Zum Sprachgebrauch. Wir werden in kommenden Beweisen einzelne Beweisschritte häufig mit dem Axiom vom Lineal begründen müssen. Wir werden in einem solchen Fall ggf. auch mit der Existenz und Eindeutigkeit des Streckenantragens begründen. Letzteres ist schließlich nichts anderes als der Inhalt des Axioms vom Lineal.
Existenz und Eindeutigkeit des Mittelpunktes einer Strecke,
Beweis von Satz III.1
Nachdem das Axiom vom Lineal formuliert wurde, wird es uns gelingen Satz III.1 zu beweisen.
noch einmal der Satz:
- Jede Strecke hat einen und nur einen Mittelpunkt.
Es sind also zwei Beweise zu führen:
- Existenzbeweis: Jede Strecke hat einen Mittelpunkt.
- Eindeutigkeitsbeweis: Jede Strecke hat nicht mehr als einen Mittelpunkt.
(Highlanderbeweis: Es kann nur einen geben.)
Der Existenzbeweis
- Es sei
 eine Strecke eine Strecke
- Behauptung:
- Es gibt einen Punkt auf der Strecke
 der zu den Endpunkten der zu den Endpunkten  und und  jeweils ein und denselben Abstand hat. jeweils ein und denselben Abstand hat.
- Die Behauptung noch mal:
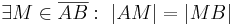 . .
Der Beweis:
Jede Strecke  hat einen Mittelpunkt. hat einen Mittelpunkt.
|
|
Beweisschritt
|
Begründung
|
| (I)
|
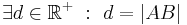
|
...
|
| (II)
|
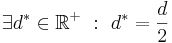
|
...
|
| (III)
|
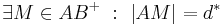
|
...
|
| (IV)
|
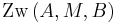 und damit und damit 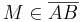
|
...
|
| (V)
|
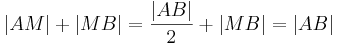
|
...
|
| (VI)
|
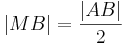
|
...
|
| (VII)
|

|
...
|
| (VIII)
|
 ist der Mittelpunkt von ist der Mittelpunkt von 
|
...
|
Der Eindeutigkeitsbeweis
Übungsaufgabe
- Hinweis: Nehmen Sie an, eine Strecke
 hätte zwei Mittelpunkte hätte zwei Mittelpunkte  und und 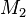 . .
den ersten Schritt kann man doch mit dem ersten Abstandsaxiom begründen.
|