Verkettung von drei Geradenspiegelungen WS 23 24

Verkettung von drei Geradenspiegelungen

Aufgabe: Welche prinzipiellen Möglichkeiten bezüglich der Lage der Achsen gibt es bei der Verkettung von drei Geradenspiegelungen? (gerne auch als Bild).

Satz X.1:

Die Verkettung von drei Geradenspiegelungen 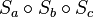$S_{a}\circ S_{b} \circ S_{c}$ an zueinander parallelen Geraden a, b und c ist eine Geradenspiegelung an einer Geraden d mit 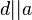$d || a$ und $\left| ab \right| =\left| dc \right|$.

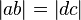Beweis:

Wie lautet der Beweis? Ich habe dazu leider nichts gefunden.--End007 (Diskussion) 14:14, 3. Feb. 2024 (CET)

End007

Kann man das so machen? --End007 (Diskussion) 14:37, 3. Feb. 2024 (CET)

Der Beweis wurde in der Vorlesung behandelt und ist auch im Video (stud.ip) zu sehen. Ihr Beweis passt soweit :-). --Schnirch (Diskussion) 09:58, 5. Feb. 2024 (CET)

Satz X.2:

Die Verkettung von drei Geradenspiegelungen 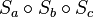$S_{a}\circ S_{b} \circ S_{c}$, an drei Geraden a, b und c die sich in einem Punkt S schneiden (kopunktal), ist eine Geradenspiegelung an einer Achse d, die durch den Punkt S verläuft mit $\left|\angle ab\right| = \left|\angle dc\right|$.

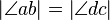Beweis:

Wie lautet der Beweis? Ich habe dazu leider nichts gefunden.--End007 (Diskussion) 14:14, 3. Feb. 2024 (CET)

Der Beweis wurde in der Vorlesung behandelt und ist auch im Video (stud.ip) zu sehen. Ihr Beweis passt soweit :-).--Schnirch (Diskussion) 09:59, 5. Feb. 2024 (CET) 

End007

Kann man das so machen? --End007 (Diskussion) 14:40, 3. Feb. 2024 (CET)

Definition X.1 (Schub- oder Gleitspiegelung)

Eine Schub- oder Gleitspiegelung ist eine Abbildung, die bei der Verkettung dreier Geradenspiegelungen 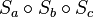$S_{a}\circ S_{b} \circ S_{c}$ entsteht, wenn die zwei Geraden a und b parallel zueinander und die dritte Gerade c senkrecht dazu steht.

Experimentieren Sie mit der nachfolgenden GeoGebra-Applikation. Welche Eigenschaften der Schubspiegelung entdecken Sie?

Falls nichts angezeigt wird, können Sie mit folgendem Link den Servercache leeren.

Satz X.3:

Die Verkettung dreier Geradenspiegelungen, deren Achsen nicht alle parallel zueinander oder kopunktal sind, ist stets eine Schubspiegelung.
Beweis: