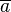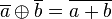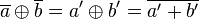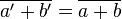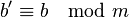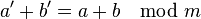Vorbereitung auf die Konferenz am 20.04.2020 10 Uhr Algebra
Das ArbeitsblattPlatz für Lösungen zu den AufgabenAufgabe 1.1eingegebene Lösunga=pm+r und b=qm+r mit 0≤r≤m a-b=pm-qm=m*(p-q) => m|(a-b) Kommentar M.G.Der Beweis ist richtig. Ich schreibe ihn hier mal noch etwas ausführlicher auf. BeweisaufgabeMan beweise: Wenn Voraussetzung
Behauptung
BeweisWir übersetzen die Voraussetzung: Aufgabe 1.2a=pm+r1 und b=qm+r2 mit 0≤r≤m und r1≠r2 Aufgabe 1.3Z5 [0 Überstrich, 1 Überstrich, 2 Überstrich, 3 Überstrich, 4 Überstrich] Die Menge enthält die Restklassen von Z5. Die Restklassen sind Teilmengen der ganzen Zahlen und bilden eine sog. Klasseneinteilung der Menge Z. Jede ganze Zahl findet sich höchstens in einer der Teilmengen wieder. Aufgabe 1.4c=(3a+2)+(3b+1)=3a+3b+3=3|c Aufgabe 1.5Aufgabe 1.6Das + im Kreis steht für die Addition von 2 Restklassen. das + ohne Kreis steht für die Addition von a und b, davon nehmen wir die Restklasse. Aufgabe 1.7Lösung 1a Überstrich + (im Kreis) b Überstrich = a+b Überstrich a Überstrich + (im Kreis) b Überstrich = a' +(im Kreis) b' = a'+b' Überstrich zz. a'+b' Überstrich = a+b Überstrich a' ist identisch zu a mod m und b' ist identisch zu b mod m. Wegen a'+b' = a+b mod m gilt: a'+b' Überstrich = a+b Überstrich. Lösung 2Kleine Hilfe zum Schreiben mathematischer Formeln und Ausdrücke im Wiki:
Hier ein paar Übersetzungen
(I) a Überstrich + (im Kreis) b Überstrich = a+b Überstrich (II) a Überstrich + (im Kreis) b Überstrich = a' +(im Kreis) b' = a'+b' Überstrich (III) zz. a'+b' Überstrich = a+b Überstrich (IV) a' ist identisch zu a mod m und b' ist identisch zu b mod m. (V)Wegen a'+b' = a+b mod m (VI) gilt: a'+b' Überstrich = a+b Überstrich. (I) Hinweis: Ich habe wortwörtlich übersetzt, damit man besser sehen kann wie der Beweis läuft. Ob der Beweis ein echter Beweis ist? Aufgabe 1.8Aufgabe 1.9In 8-Bit-Bildern sind bis zu 256 Graustufen enthalten. Helligkeitswerte: 0=Schwarz; 255=Weiß Aufgabe 1.10Nachbearbeitung des Meetings vom 20.04.Das Whiteboard
Fragen von M.G. zur technischen QualitätIch brauche ein wenig Rückkopplung: Um die Lesbarkeit Ihrer Mitschriften zu verbessern, ist es vielleicht sinnvoll, ein Hintergrundraster (z.B. Hybrid) im Whiteboard anzeigen zu lassen. Wie war der TonSchlechter Ton ist anstrengend. Ich habe extra ein sehr gutes Mikro besorgt, weiß aber nicht ob es gut eingestellt war für den Zweck. Der Ton war gut. Allerdings ist es wichtig, dass alle Teilnehmer*innen - bis auf Sie - das Mikrofon ausstellen! BildqualitätIch nehme extra einen kleinen Rechner mit recht geringer Bildschirmauflösung für die Meetings. Es hätte ja keinen Sinn, wenn ich mit enem Superbildschirm arbeite, auf vielen Endgeräten dann jedoch kaum noch was zu erkennen ist. War alles lesbar, was wäre zu verbessern? (grüne Tafel und Kreide sind durch nichts zu ersetzen). Fragen zum LehrstoffWas ist unklar, worauf muss ich beim nächsten mal unbedingt eingehen, wozu wäre ein Erkärvideo nützlich? Fühlen Sie sich frei hier Ihre Fragen zu stellen: Frage 1Wie werden Fotos oder Pdfs in Wiki eingefügt? Frage 2Frage 3.... |

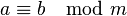 , dann
, dann 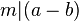 .
.
 und
und  bei Division durch
bei Division durch  denselben Rest
denselben Rest  lassen.
lassen.  und
und 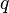 derart, dass
derart, dass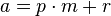 und
und 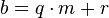 mit
mit 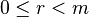 gilt.
gilt.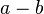 ist,
ist, mit
mit 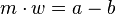 gibt.
gibt.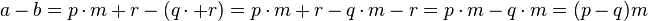
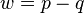 und haben damit gezeigt, dass
und haben damit gezeigt, dass