Was wird Lisa ihre Schüler wohl spannen lassen?
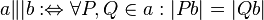Winkelkreuz und das Kriterium zusammen betrachten, worum kann es in Aufgabe 3 alte PO nur gehen?
Na ganz klar, es geht um "echte" Paralleogramme und "echte" Rechtecke mit a=c>b=d !!!
ROFL
Didaktischer Kommentar: "Paradoxer Impuls durch Ironie"
--Just noch ein sailA 20:44, 22. Jul. 2012 (CEST)
Aber unsere Diagonalen stehen senkrecht zueinander. Bin mir nicht ganz sicher, würde aber sagen, dass Kriterium gehört zu der Raute.
--H2O 21:07, 22. Jul. 2012 (CEST)
Bin der Meinung, dass es nur um die Raute oder das Quadrat gehen kann.
Im Rechteck und im Parallelogramm stehen die Diagonalen nicht senkrecht aufeinander und können somit im Heidelberger Winkelkreuz nicht gespannt werden ..
(außer Spezialfall: Quadrat bzw. Raute!)
Gilt das Kriterium für 2 Paar gegenüberliegende Seiten??..dann muss es das Quadrat sein!
Wenn nicht, dann könnte es sogar noch der Spezialfall gl. Trapez mit senkrecht aufeinander stehenden Diagonalen sein......! Oje oje :(
--Tchu Tcha Tcha 21:30, 22. Jul. 2012 (CEST)
!-> ich glaub auch eher, dass es sich um ein gleichschenkliges Trapez handelt. Vlt sollten wir den korrekten Beweis hierfür noch in den Spickzettel mit aufnehmen.
Spaßvogel Just noch ein sailA :-) ich würde sagen es handelt sich eher um ein gemeines Kreisviereck ;-) --LuLu7410 21:16, 22. Jul. 2012 (CEST)
Beim Quadrat fehlt aber, dass die diagonal gleich lang sind, somit müßte Raute stimmen. --H2O 21:41, 22. Jul. 2012 (CEST)
natürlich sind die diagonalen im quadrat gleich lang.... wers noch nicht gecheckt hat: das vom saila war ein scherz :-) ansonsten ROFL googeln :-p möglich sind spezielle gleichschenkl. trapeze, quadrate und rauten.... die ja letztes semester schon dran waren. --LuLu7410 21:46, 22. Jul. 2012 (CEST)
also ich hätte gleichschenkliges trapez gesagt, aber ich versteh die aussage nicht ganz !!--Celebino 23:04, 22. Jul. 2012 (CEST) Also habe nochmal nachgeschaut und bin derselben Meinung wie LuLu. Es kommen spezielle gleichschenkl. Trapeze, quadrate und rauten in frage......habe es so verstanden dass es darum geht dass zwei geraden nur dann parallel zueinander sind wenn gilt, dass jeder abstand dieser beiden geraden gleich sein muss ^^ so irgendwie halt :(--Celebino 23:37, 22. Jul. 2012 (CEST)
mehr kann ich wirklich nicht verraten --*m.g.* 23:46, 22. Jul. 2012 (CEST)
Nun ist die Katze ja aus dem Sack :D --Celebino 23:50, 22. Jul. 2012 (CEST)
Welche Katze ist aus dem Sack? Ich wüsste jetzt nicht, was ich heute nochmal explizit anschauen sollte. Kann mir jemand auf die Sprünge helfen? Sitze seit 06:30 am Rechner und zerbreche mir den Kopf :( Der Beweis, dass die Geraden parallel sind, wenn der Abstand gleich ist, ist ja genau das Parallelenkriterium und das werde ich ja wohl nicht beweisen sollen. Wie kann ich es mit den doofen gl. Trapezen in Einklang bringen? =((--*osterhase* 07:31, 23. Jul. 2012 (CEST)
Achte mal drauf was senkrecht ist bei den verschiedenen Trapeze, mal sind es Diagonalen und mal stehen Seiten senkrecht zueinander ,vielleicht ist das wichtig. --Just noch ein sailA 08:09, 23. Jul. 2012 (CEST)
Bei der Aussage handelt es sich um das parallelenkriterium --H2O 23:37, 22. Jul. 2012 (CEST)
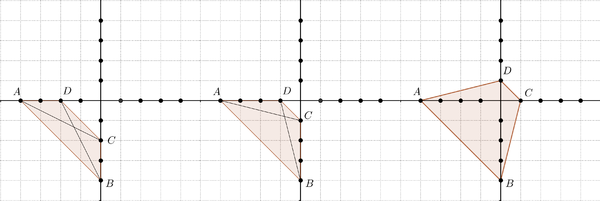
@Just noch ein sailA: Was meinst du mit "die Seiten stehen senkrecht aufeinander"? ich sehe nur in Abb.3 die Diagonalen, die durch das Winkelkreuz senkrecht stehen...--Sissy66
13:44, 23. Jul. 2012 (CEST)
@sissy66 schau dir Abbildung 1 und 2 an, wenn die Seiten AD und AC verlängerst, dann siehst du dass die Strecken senkrecht zueinander stehen. Nicht schneiden, aber senkrecht zueinander stehen.--Just noch ein sailA 14:21, 23. Jul. 2012 (CEST)
Schön, schön und was bitte sollen wir damit in der Klausur anfangen..?!? :)
Denke, da geht's um was anderes..--Tchu Tcha Tcha 14:47, 23. Jul. 2012 (CEST)
@Tchu Tcha Tcha Was weiß der Geier?? Zum Beispiel kannst du aus dem gl.Trapez ABCD das Dreieck ABM(Mittelnippel Winkelkreuz machen)und Thales zum spielen einladen oder die Winkelkreuz Spezialdefi für gl.Trapez benutzen: ABCD sei ein Viereck mit zwei parallelen Seiten und zwei senkrecht zueinander stehenden Seiten ist gl. Trapez. Du musst auch nix mit machen was du nicht willst, aber wenn man es schonmal sieht kann es ja nicht schaden. Es könnte auch helfen auf die Def:ABCD ein Viereck mit zwei parallelen Seiten und an einer der Parallelen anliegenden kongruenten Innenwinkel ist ein gl. Trapez.zu verstehen. Alles kann nichts muss ;-) Liebe Grüsse--Just noch ein sailA 16:19, 23. Jul. 2012 (CEST)
@sailA ajooo, bin dabei.. :) haha ;)--Tchu Tcha Tcha 18:17, 23. Jul. 2012 (CEST)
Habe heute mit der Übung auch nicht so recht etwas anfangen können. Es geht definitiv um eine bestimmte Vierecksart, das ist natürlich klar geworden. Aber was ich daran wie beweisen soll und mit welchen Grundeigenschaften ich nun arbeiten soll (wenn nun doch nicht mehr senkrecht) dann bin ich jetzt auch am Ende des Lateins. Vll könnte sich *m.g* nochmal dazu äußern??
na, vermutlich werden wir nicht alles vorgekaut bekommen und ich geh mal davon aus, dass die grundeigenschaften, mit denen wir arbeiten sollen aus tätigkeit 1 und tätigkeit 2 hervorgehen, die lisas schüler am winkelkreuz tätigen sollen.... --LuLu7410 16:16, 23. Jul. 2012 (CEST)
@Just noch ein sailA: danke..jetzt hab ich´s auch endlich verstanden..naja, lieber später, als nie :D! mich hat heute etwas verwirrt, dass wir "anscheinend" das Parallelogramm rausnehmen, aber laut der gegebenen Eigenschaften, es doch nicht draußen ist..hat da jemand ne´Idee, was gemeint war..!?!?--Sissy66 16:50, 23. Jul. 2012 (CEST)
