Winkelmaß, Rechte Winkel SoSe 13
Aus Geometrie-Wiki
Inhaltsverzeichnis |
Das Winkelmaß
Was bedeutet es, die Größe eines Winkels zu messen?
| Länge einer Strecke | Größe eines Winkels |
| nichtnegative reelle Zahl | reelle Zahl zwischen 0 und 180 |
Definition IV.6 : (Winkelmaß)
- Jedem Winkel
 kann genau eine reelle Zahl
kann genau eine reelle Zahl 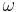 zwischen 0 und 180 zugeordnet werden. Diese Zahl wird als Größe oder als Maß des Winkels
zwischen 0 und 180 zugeordnet werden. Diese Zahl wird als Größe oder als Maß des Winkels  bezeichnet.
bezeichnet.
In Zeichen: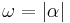 .
.
- Jedem Winkel
Wie aus der Schule bekannt, lassen sich Winkelgrößen addieren oder auch subtrahieren:
Satz IV.1
- Wenn der Punkt
 im Inneren des Winkels
im Inneren des Winkels  und nicht auf einem der Schenkel des Winkels
und nicht auf einem der Schenkel des Winkels  liegt, dann ist die Größe der beiden Teilwinkel
liegt, dann ist die Größe der beiden Teilwinkel 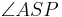 und
und 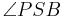 jeweils kleiner als die Größe des Winkels
jeweils kleiner als die Größe des Winkels  .
.
- Wenn der Punkt
Beweis von Satz IV.1
Für diesen Beweis benötigen wir spezielle Winkelaxiome, auf die wir an dieser Stelle aber verzichten wollen.
Rechte Winkel
Definition IV.2 : (Rechter Winkel)
- Wenn ein Winkel die selbe Größe wie einer seiner Nebenwinkel hat, so ist er ein rechter Winkel.
Definition IV.3 : (Supplementärwinkel)
- Zwei Winkel heißen supplementär, wenn die Summe ihrer Größen 180 beträgt.
Satz IV.2:
- Nebenwinkel sind supplementär.
Satz IV.3a :
- Jeder rechte Winkel hat das Maß 90.
Beweis von Satz IV.3a :
- Übungsaufgabe
- Übungsaufgabe
Satz IV.3b :
- Jeder Winkel, der das Maß 90 hat ist ein rechter Winkel.
Beweis von Satz IV.3b :
- Übungsaufgabe
- Übungsaufgabe
Wir haben somit in der Aussage, das Maß 90 zu haben, eine hinreichende und notwendige Bedingung dafür gefunden, ein rechter Winkel zu sein und damit ein Kriterium für einen rechten Winkel gefunden. Dieses Kriterium eignet sich somit als neue Definition des Begriffs "rechter Winkel":
Definition IV.4 : (Rechter Winkel)
Die Relation Senkrecht auf der Menge der Geraden
Definition IV.5 : (Relation senkrecht auf der Menge der Geraden)
- Es seien
 und
und  zwei Geraden. Wenn sich
zwei Geraden. Wenn sich  und
und  schneiden und bei diesem Schnitt rechte Winkel entstehen, dann stehen die Geraden
schneiden und bei diesem Schnitt rechte Winkel entstehen, dann stehen die Geraden  und
und  senkrecht aufeinander.
senkrecht aufeinander.
- Es seien
- In Zeichen:
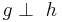 (in der Formelbeschreibungssprache Tex: \perp , läßt sich gut merken, von perpendicular)
(in der Formelbeschreibungssprache Tex: \perp , läßt sich gut merken, von perpendicular)
- In Zeichen:
Definition IV.6 : (noch mehr Senkrecht)
- Eine Gerade
 und eine Strecke
und eine Strecke  stehen senkrecht aufeinander, wenn
stehen senkrecht aufeinander, wenn  und die Gerade
und die Gerade  senkrecht aufeinander stehen.--Nolessonlearned 09:31, 16. Jul. 2013 (CEST)
senkrecht aufeinander stehen.--Nolessonlearned 09:31, 16. Jul. 2013 (CEST)
- Eine Gerade
Korrekt.--Tutorin Anne 14:30, 16. Jul. 2013 (CEST)

