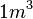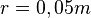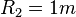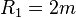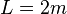Version vom 3. Januar 2012, 13:14 Uhr

Das Gast-Wiki im Geo-Wiki: Didaktik der anwendungsbezogenen Mathematik

Ideensammlung

• Auf dem Königsstuhl in Heidelberg

• Proportionalität am Menschen

• Spezifische Wärmekapazität von Wasser

• Windrad

• Riesenrad

• Stauaufgabe

Funktionales Denken

Lineare Funktionen

• Beispielaufgaben

Proportionalität

• Größenbereiche
• Definition der Proportionalität
• Die Eigenschaften der Proportionalität nach Fricke
• Beispiele für Proportionale Zusammenhänge

Quadratische Zusammenhänge

• Wurfparabel

• Klippenspringer

• Schwimmbad

Was ist, was soll Sachrechnen

Sachrechnen

Folien vom 18.11. als PDF (mit Office 2010 hat es dann doch geklappt.) Sachrechnen

Def. Sachrechnen (aus Greefrath. 2010. S. 12)
"Sachrechnen im weiteren Sinne bezeichnet die Auseinandersetzung mit der Umwelt, sowie die Beschäftigung mit wirklichkeitsbezogenen Aufgaben im Mathematikunterricht."
--Löwenzahn 16:24, 27. Nov. 2011 (CET)

Funktionen des Sachrechnens nach Winter

Sachrechnen als Lernstoff

Die mathematischen Inhalte des Sachrechnens stehen im Vordergrund. Greefrath setzt vorallem den Schwerpunkt auf die Inhalte der Größen, des Prozent- und Zinsrechnens. Allerdings ist der Inhalt stark davon abhängig wie der Mathematikunterricht gestaltet wird. Das Wichtige dabei ist, dass ein realitätsbezogener Kontext vorliegt. (Vgl. Greefrath. 2010. S. 13)
--Löwenzahn 16:31, 27. Nov. 2011 (CET)

Vermittlung von Größenvorstellungen

Längen

Stützpunktvorstellung:

• 1cm: Nagel kleiner Finger / zwei Rechenkästchen im Heft
• 20 cm: Handspanne
• 100 m: Länge Fussballfeld

SuS selbst messen lassen, entweder mit Metermaß oder vergleichbarer Einheit, zB Rechenkästchen im Heft:

• Bleistift
• Klassenzimmer (lang)
• Mäppchen

Flächeninhalte

Stützpunktvorstellung:

• 1a: Familienwohnung
• 1km²: Industrieareal
• 1m²: Tafel

SuS selbst messen lassen:

• Wie groß ist der Basketballplatz der Schule?
• SuS schätzen 10m² Fläche und legen diese mit einem Seil als Begrenzung.

Volumina

Zeit

Stützpunktvorstellung:

• 1s = zählen 21,22,23...
• 45 min = eine Schulstunde / Halbzeit Fußball

SuS selbst messen lassen:

• Zeit abschätzen lassen: Wann sind 10 Sekunden, 20... vergangen?

Massen

• 1oog: Tafel schokolade

• 1kg: Packung Mehl / zwei Senfgläser

• 10kg: Eimer Wasser

Gewichte

Sützpunktvorstellungen

• Tafel Schokolade
• Flasche 1l Wasser

SuS selbst messen lassen

• verschieden starke Federkraftmesser verwenden --> Mäppchen messen

Frage:Wenn sich (freiwillige)SuS mittels analoger Personenwaage wiegen würde, gehört das dann zum Gewicht oder zur Masse?--Löwenzahn 13:23, 15. Dez. 2011 (CET)

Wir hatten ja gesagt, dass die selbe Personenwaage auf dem Mond zum Beispiel eine andere Gewichtskraft als auf der Erde anzeigt. Deshalb müsste die Waage also korrekterweise als Gewichtskraftmesser beszeichnet werden. Das Bestimmen einer Masse ist nur durch Vergleich mit bekannten Massestücken auf einer echten Waage möglich.--Prayush 21:12, 15. Dez. 2011 (CET)

Geschwindigkeiten

Stützpunktvorstellung

• Geschwindigkeit eines Autos in der Stadt (50km/h)
• Geschwindigkeit einer Kugel in Öl

SuS selbst messen lassen

• Geschwindkeitsmessung einer Kugel im Rohr
• Wie schnell rennt ein SuS 100m, 50m...?
• Wie lange brauchen die SuS für den Nachhauseweg?

Dichten

Stützpunktvorstellung

• Bernstein schwimmt im Meerwasser, Stein sinkt
• Holz treibt auf dem Wasser

SuS messen lassen

• Welche Dichte besitzt ein beliebiger Stein? --> Gewicht/Volumen (kg/m³) Überlaufmethode: Wieviel Wasser wird verdrängt = Volumen
• Messgeräte verwenden: Aräometer, Pyknometer

Informationen

(Byte, GB,

Stützpunktvorstellung

• maximale Anzahl an MP3 (Bilder, Filme..) Dateien auf USB-Stick, CD, Festplatte...

SuS selbst entdecken lassen

• Wie viele 1GB USB-Sticks kann ich durch eine Terabyte Festplatte ersetzen?
• SuS brennen maximale Anzahl an MP3s auf eine CD, DCD, Blueray
• Wie viele bits stecken hinter einem Byte?

Sachrechnen als Lernprinzip

Wird Sachrechnen unter dem Aspekt des Lernprinzipes betrachtet, "so werden Sachsituationen beispielsweise zur Motivation, Veranschaulichung oder zur Übung mathematischer Lernprozesse genutzt. Hier steht die Arbeit der SuS im Vordergrund, die mathematische Inhalte mit Hilfe von realen oder wirklichkeitsnahen Situationen lernen." (Greefrath, 2010, S. 13) --Löwenzahn 13:07, 3. Jan. 2012 (CET)

Sachrechnen als Lernziel

Die Beschäftigung mit der Umwelt selbst wird als Lernziel betrachtet. Dies ist die allgemeinste Funktion des Sachrechnens. Die "Sache und nicht das Rechnen [steht] im Mittelpunkt des Lernprozesses". Durch mathematische Mittel und Methoden soll die Umwelt verstanden und erklärt werden. "Das Ziel des Sachrechnens ist unter diesem Aspekt die Befähigung zur Wahrnehmung und zum Verstehen von Erscheinungen unserer Welt." (Greefrath, 2010,S. 15)--Löwenzahn 13:14, 3. Jan. 2012 (CET)

Komplexität von Sachrechenaufgaben

Simplex

Unter einem Simplex versteht man eine Struktur vom folgenden Typ:

Zwei Eingabedaten wird durch deren Verknüpfung mittels einer Rechenoperation ein Ausgabedatum zugeordnet.

Komplex

Unter einem Komplex versteht man die Verkettung mehrerer Simplexe. Man unterscheidet linerare und verzweigte Komplexe.

linearer Komplex

Verzweigter Komplex

Modellierung

Realsituation

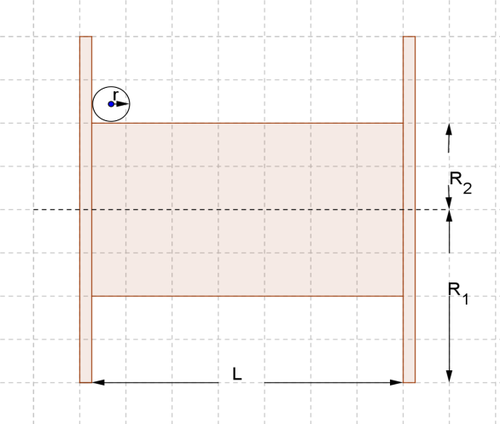
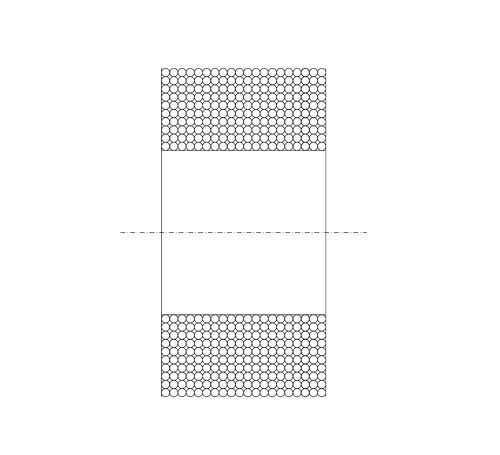
Wieviel m Kabel passt auf die Trommel?

Realmodell

Schätzung:

Lauter Kreise Modell

mathematisches Modell

Kalkulationstabelle

Formel

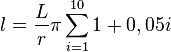
Validierung des mathematischen Modells

Übungsaufgaben

Modellierung

• Rübenlaster
• Parabel_Brücke_Transporter

Körperberechnung

Köln-Triangle

Alte Klausuren und Probeklausuren

{{{2}}}

Übungsaufgaben im Hinblick auf die Klausur

Bahnfahren

"Sehr geehrte Damen und Herren, wir begrüßen die neu zugestiegenen Fahrgäste im ICE 617 auf unserer Fahrt von Frankfurt am Main Flughafen nach Stuttgart Hauptbahnhof. Bitte beachten Sie in Stuttgart, dass unser neues Bahnhofsprojekt dort bereits für viel Lärm gesorgt hat und verhalten Sie sich beim Verlassen des Zuges leise.
Leider müssen wir Ihnen mitteilen, dass wir aufgrund einer Verzögerung im Betriebsablauf eine Verspätung von fünf Minuten haben und der vor uns liegende Streckenabschnitt noch durch einen vorausfahrenden Zug belegt ist. Wir werden unsere Fahrt in Kürze fortsetzen.
Leider ist die Strecke nach Mannheim durch einen Gleisschaden im Moment nicht befahrbar. Daher werden wir eine alternative Route wählen. Diese führt uns über Mainz nach Mannheim. Wie sie sicherlich bemerkt haben, pfeifft unser ICE 1 bereits jetzt aus dem letzten Loch und aus diesem Grunde können wir über Mainz auch nicht schneller nach Mannheim fahren als wie direkt von Frankfurt am Main Flughafen aus.
Da wir uns in den nächsten Jahren mit neuen 'ICx'-Zügen ausstatten, bitten wir die Unannehmlichkeiten zu entschuldigen und als Entschädigung dürfen Sie sich ein Teil des ICE mit nach Hause nehmen. Wer das Gefühl hat, dass er seinen Anschlusszug nicht erreicht, darf sich die Lok des Zuges mitnehmen und damit nach Hause fahren. Vielen Dank für Ihre Aufmerksamkeit und gute Nacht!"

Muss der Passagier mit der folgenden Fahrkarte alleine mit der Lok nach Hause fahren?


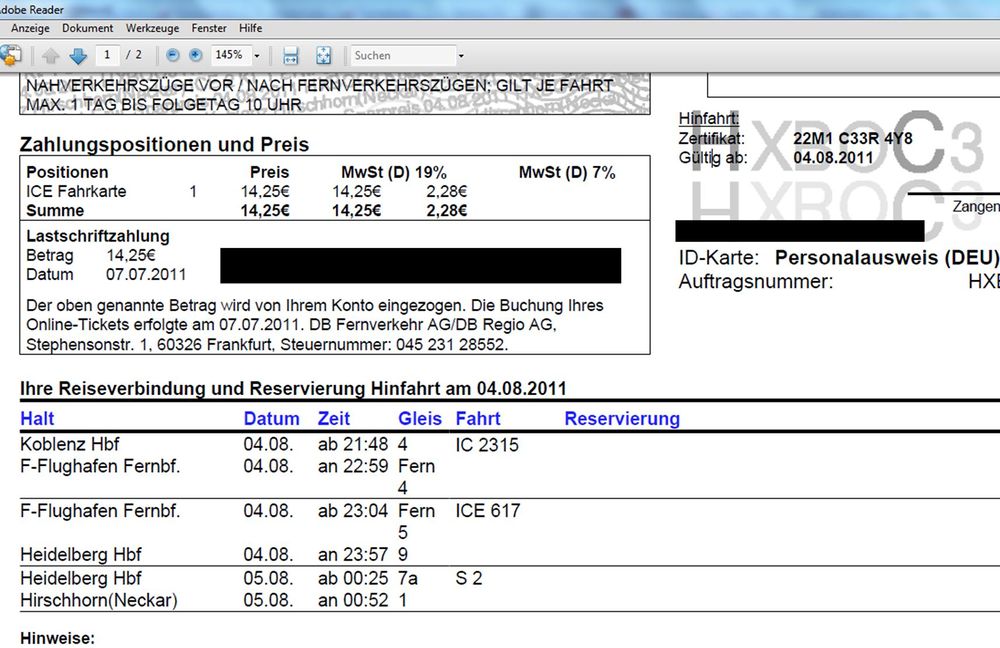
--Flo60 20:46, 2. Jan. 2012 (CET)