Lösung von Aufg. 14.4 (WS 11/12: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
Zeile 1: Zeile 1:
 
Schauen Sie sich das nachfolgende Applet an und bewegen Sie die Figur am Punkt Z.<br />
 
Schauen Sie sich das nachfolgende Applet an und bewegen Sie die Figur am Punkt Z.<br />
 
a) Welche Bedingung ergibt sich für den dargestellten Winkel <math>\angle MAB</math>, wenn die Gerade ''g'' zur Tangente am Kreis ''k'' im Punkt ''A'' wird?<br /><br />
 
a) Welche Bedingung ergibt sich für den dargestellten Winkel <math>\angle MAB</math>, wenn die Gerade ''g'' zur Tangente am Kreis ''k'' im Punkt ''A'' wird?<br /><br />
−
Der Winkel <math>\angle MAB</math> wird zum rechten Winkel, <math>MAB \ \perp \ g</math> --[[Benutzer:Phhd mat|Phhd mat]] 11:12, 30. Jan. 2012 (CET)<br /><br />
+
Der Winkel <math>\angle MAB</math> wird zum rechten Winkel, <math>MAB \ \perp \ g</math> --[[Benutzer:Phhd mat|Phhd mat]] 11:12, 30. Jan. 2012 (CET)<br />
 +
 
 +
<br />Also genau genommen verschwindet der Winkel <math>\angle MAB</math>, da der Punkt A und B identisch ist. Es müsste also heißen: <math>\angle MAZ \ \perp \ g</math><br />
 +
 
 +
 
 +
<br />
 
b) Ergänzen Sie mit der Erkenntnis aus a) den folgenden Satz: Wenn eine Gerade ''g'' Tangente an einem Kreis ''k'' im Berührpunkt ''A'' ist, dann ...<br /><br />
 
b) Ergänzen Sie mit der Erkenntnis aus a) den folgenden Satz: Wenn eine Gerade ''g'' Tangente an einem Kreis ''k'' im Berührpunkt ''A'' ist, dann ...<br /><br />
 
...steht der Radius <math>\overline{MA} </math>senkrecht auf ''g'' --[[Benutzer:Phhd mat|Phhd mat]] 11:12, 30. Jan. 2012 (CET)<br /><br />
 
...steht der Radius <math>\overline{MA} </math>senkrecht auf ''g'' --[[Benutzer:Phhd mat|Phhd mat]] 11:12, 30. Jan. 2012 (CET)<br /><br />

Version vom 31. Januar 2012, 19:24 Uhr

Schauen Sie sich das nachfolgende Applet an und bewegen Sie die Figur am Punkt Z.
a) Welche Bedingung ergibt sich für den dargestellten Winkel 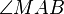\angle MAB, wenn die Gerade g zur Tangente am Kreis k im Punkt A wird?

Der Winkel 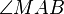\angle MAB wird zum rechten Winkel, 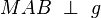MAB \ \perp \ g --Phhd mat 11:12, 30. Jan. 2012 (CET)


Also genau genommen verschwindet der Winkel 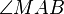\angle MAB, da der Punkt A und B identisch ist. Es müsste also heißen: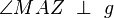 \angle MAZ \ \perp \ g



b) Ergänzen Sie mit der Erkenntnis aus a) den folgenden Satz: Wenn eine Gerade g Tangente an einem Kreis k im Berührpunkt A ist, dann ...

...steht der Radius 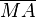\overline{MA} senkrecht auf g --Phhd mat 11:12, 30. Jan. 2012 (CET)

c) Beweisen Sie den Satz aus b) indirekt.

Voraussetung: g Tangente an k, 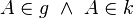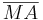A \in g \ \wedge \ A \in k, \overline{MA} ist Radius
Behauptung: 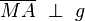\overline{MA} \ \perp \ g
Annahme: 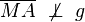\overline{MA} \ \not\perp \ g
(1) Es existiert ein Lot mit der Eigenschaft 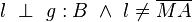\ l \ \perp \ g: {B} \ \wedge \ l \neq \overline{MA}
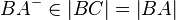
(2) Antragen Punkt C auf Strahl \ BA^{-} \in \left| BC \right| = \left| BA \right|
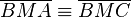(3) \overline{BMA} \equiv \overline{BMC} nach SWS
(4) 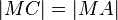\left| MC \right| = \left| MA \right| nach 3. und Dreieckskongruenz
(5) 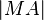\left| MA \right| ist Radius nach Vorausssetzung
(6) 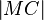\left| MC \right| ist ebenfalls Radius nach 4. und 5.
(7) 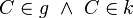C \in g \ \wedge \ C \in k nach 6.
Widersprung zur Voraussetung!--Phhd mat 11:12, 30. Jan. 2012 (CET)

d) Gilt auch die Umkehrung des Satzes aus b)? Beweisen Sie dies.

e) Entwickeln Sie ein Tangentenkriterium aus b) und d)


Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufg._14.4_(WS_11/12&oldid=10942“