Übung Aufgaben 5 S (SoSe 12): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
Wokkow (Diskussion | Beiträge) K (→Aufgabe 5.2) |
HecklF (Diskussion | Beiträge) (→Aufgabe 5.5) |
||
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 16: | Zeile 16: | ||
<br /><br /> | <br /><br /> | ||
[[Lösung von Aufgabe 5.2_S (SoSe_12)]] | [[Lösung von Aufgabe 5.2_S (SoSe_12)]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==Aufgabe 5.3== | ==Aufgabe 5.3== | ||
| Zeile 62: | Zeile 38: | ||
Beweisen Sie: Je vier nicht komplanare Punkte sind paarweise verschieden (Hinweis: Nutzen Sie bei der Beweisführung die Sätze aus Aufgabe 4.3 und Zusatzaufgabe 4.4).<br /><br /> | Beweisen Sie: Je vier nicht komplanare Punkte sind paarweise verschieden (Hinweis: Nutzen Sie bei der Beweisführung die Sätze aus Aufgabe 4.3 und Zusatzaufgabe 4.4).<br /><br /> | ||
[[Lösung von Aufg. 5.5_S (SoSe_12)]]<br /> | [[Lösung von Aufg. 5.5_S (SoSe_12)]]<br /> | ||
| + | <br /> | ||
| + | [[Lösungsideen Übung Heckl 23.05.2012]] | ||
[[Category:Einführung_S]] | [[Category:Einführung_S]] | ||
Aktuelle Version vom 23. Mai 2012, 20:22 Uhr
Inhaltsverzeichnis |
Aufgaben zum Abstand
Aufgabe 5.1
Satz:
- Von drei paarweise verschiedenen Punkten
 und
und  ein und derselben Geraden
ein und derselben Geraden  liegt genau einer zwischen den beiden anderen.
liegt genau einer zwischen den beiden anderen.
- Von drei paarweise verschiedenen Punkten
Beweisen Sie diesen Satz.
Lösung von Aufgabe 5.1_S (SoSe_12)
Aufgabe 5.2
Zeigen Sie, dass für drei paarweise verschiedene Punkte  und
und  gilt:
gilt:





Tipps zu Aufgabe 5.2 (SoSe_12)
Lösung von Aufgabe 5.2_S (SoSe_12)
Aufgabe 5.3
Zeigen Sie, dass für drei paarweise verschiedene Punkte  und
und  gilt:
gilt:
Wenn 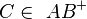 und
und 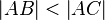 dann gilt
dann gilt 
Lösung von Aufgabe 5.3_S (SoSe_12)
Aufgabe 5.4
Beweisen Sie: Zu jeder Strecke  existiert genau eine Strecke
existiert genau eine Strecke  auf
auf  mit
mit 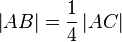 und
und 


Tipps zu Aufgabe 5.4 (SoSe_12)
Lösung von Aufgabe 5.4_S (SoSe_12)
Weitere Aufgabe zur Inzidenz
Aufgabe 5.5
Beweisen Sie: Je vier nicht komplanare Punkte sind paarweise verschieden (Hinweis: Nutzen Sie bei der Beweisführung die Sätze aus Aufgabe 4.3 und Zusatzaufgabe 4.4).
Lösung von Aufg. 5.5_S (SoSe_12)
Lösungsideen Übung Heckl 23.05.2012

