Übung 8: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Aufgabe 8.1) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 8.1) |
||
| Zeile 1: | Zeile 1: | ||
== Aufgabe 8.1 == | == Aufgabe 8.1 == | ||
| − | Es sei <math>\ \ | + | Es sei <math>\ \Epsilon</math> eine Ebene, die durch die Gerade <math>\ g</math> in die beiden Halbebenen <math> gQ^+</math> und <math>gQ^-</math> eingeteilt wird. Ferner sei <math>\ R</math> ein Punkt der Halbebene <math>\ gQ^-</math>, der nicht auf der Trägergeraden <math>\ g</math> liegen möge. |
Beweisen Sie: <math>\ gR^+ \equiv gQ^-</math> und <math>\ gR^- \equiv gQ^+ </math> | Beweisen Sie: <math>\ gR^+ \equiv gQ^-</math> und <math>\ gR^- \equiv gQ^+ </math> | ||
Version vom 12. Juni 2010, 08:35 Uhr
Inhaltsverzeichnis[Verbergen] |
Aufgabe 8.1
Es sei 
eine Ebene, die durch die Gerade 
in die beiden Halbebenen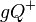 
und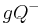 
eingeteilt wird. Ferner sei 
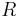ein Punkt der Halbebene 
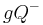, der nicht auf der Trägergeraden liegen möge.
Beweisen Sie: 
und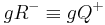 
Aufgabe 8.2
Beweisen Sie: Es gibt rechte Winkel und jeder rechte Winkel hat das Maß 90.
Aufgabe 8.3
Beweisen Sie:
Wenn 
und 
zwei Scheitelwinkel sind, dann haben und dieselbe Größe.
Aufgabe 8.4
Beweisen Sie die Existenz und Eindeutigkeit der Mittelsenkrechten.
Aufgabe 8.5
Definieren Sie die Begriffe Stufenwinkel und Wechselwinkel (an geschnittenen Geraden).
