Übung 8

Aufgabe 8.1

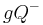Es sei $\ \Epsilon$ eine Ebene, die durch die Gerade $\ g$ in die beiden Halbebenen $\ gQ^+$ und $\ gQ^-$ eingeteilt wird. Ferner sei 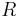$\ R$ ein Punkt der Halbebene 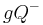$\ gQ^-$, der nicht auf der Trägergeraden $\ g$ liegen möge. Beweisen Sie: $\ gR^+ \equiv gQ^-$ und $\ gR^- \equiv gQ^+$

Lösung von Aufgabe 8.1

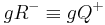
Aufgabe 8.2

In der Vorlesung haben wir die Repräsentantenunabhängigkeit des Referenzpunktes zweier Halbebenen gezeigt. Verdeutlichen Sie den Zusammenhang zur Klasseneinteilung der Ebene.

Lösung von Aufgabe 8.2

Aufgabe 8.3

Entwerfen Sie jeweils ein Arbeitsblatt zur induktiven Erarbeitung der Begriffe Nebenwinkel und Scheitelwinkel mit Schülern der SI. Definieren Sie die Begriffe Nebenwinkel und Scheitelwinkel dann schülergerechter als im Skript.

Lösung von Aufgabe 8.3

Aufgabe 8.4

Definieren Sie den Begriff des Dreiecks, den Begriff des Innenwinkel eines Dreiecks und den Begriff des Inneren eines Dreiecks.

Lösung von Aufgabe 8.4

Aufgabe 8.5

Definieren Sie: gleichschenkliges Dreieck, Schenkel eines gleichschenkligen Dreiecks, Basis eines gleichschenkligen Dreiecks, Basiswinkel eines gleicvhschenkligen Dreiecks.

Lösung von Aufgabe 8.5

Aufgabe 8.6

Definieren Sie die Begriffe Stufenwinkel und Wechselwinkel (an geschnittenen Geraden).

Lösung von Aufgabe 8.6

Aufgabe 8.7

Beweisen Sie: Das Innere eines beliebigen Dreiecks ist konvex.

Lösung von Aufgabe 8.7

Aufgabe 8.8

Zum Beweis des folgenden Satzes reichen unsere bisherigen Axiome und Sätze noch nicht aus. Beweisen Sie den Satz deshalb mit den geometrischen Kenntnissen, die Sie während Ihrer Schulzeit erworben haben.

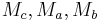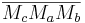Satz: Es sei $\overline{ABC}$ ein gleichseitiges Dreieck. Die Punkte $\ M_c, M_a, M_b$ seien die Mittelpunkte der Seiten von $\overline{ABC}$. Das Dreieck $\overline{M_c M_a M_b}$ ist gleichseitig.

Lösung zu 8.8