Übung 8: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Aufgabe 8.3) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 8.2) |
||
| Zeile 6: | Zeile 6: | ||
== Aufgabe 8.2 == | == Aufgabe 8.2 == | ||
| − | + | In der Vorlesung haben wir die Repräsentantenunabhängigkeit des Referenzpunktes zweier Halbebenen gezeigt. Verdeutlichen Sie den Zusammenhang zur Klasseneinteilung der Ebene. | |
[[Lösung von Aufgabe 8.2]] | [[Lösung von Aufgabe 8.2]] | ||
Version vom 12. Juni 2010, 16:06 Uhr
Inhaltsverzeichnis[Verbergen] |
Aufgabe 8.1
Es sei 
eine Ebene, die durch die Gerade 
in die beiden Halbebenen 
und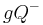 
eingeteilt wird. Ferner sei 
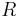ein Punkt der Halbebene 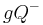, der nicht auf der Trägergeraden liegen möge.
Beweisen Sie: 
und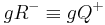 
Aufgabe 8.2
In der Vorlesung haben wir die Repräsentantenunabhängigkeit des Referenzpunktes zweier Halbebenen gezeigt. Verdeutlichen Sie den Zusammenhang zur Klasseneinteilung der Ebene.
Aufgabe 8.3
Entwerfen Sie jeweils ein Arbeitsblatt zur induktiven Erarbeitung der Begriffe Nebenwinkel und Scheitelwinkel mit Schülern der SI. Definieren Sie die Begriffe Nebenwinkel und Scheitelwinkel dann schülergerechter als im Skript.
Aufgabe 8.4
Beweisen Sie die Existenz und Eindeutigkeit der Mittelsenkrechten.
Aufgabe 8.5
Definieren Sie die Begriffe Stufenwinkel und Wechselwinkel (an geschnittenen Geraden).
