Übung 10: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(→‎Aufgabe 10.1)
(→‎Aufgabe 10.2)
Zeile 10: Zeile 10:
  
 
== Aufgabe 10.2 ==
 
== Aufgabe 10.2 ==
 +
 +
Beweisen Sie:
 +
 +
<u>Satz V.5:</u> (Existenz und Eindeutigkeit der Senkrechten zu einer Geraden auf einem Punkt dieser Geraden)<br />
 +
:: Es sei <math>\ g</math> eine Gerade der Ebene <math>\ \Epsilon</math>. Ferner sei <math>\ P</math> ein Punkt auf <math>\ g</math>. In der Ebene <math>\ \Epsilon</math> gibt es genau eine Gerade <math>\ s</math>, die durch <math>\ P</math> geht und senkrecht auf <math>\ g</math> steht.
 +
 +
[[Lösung von Aufgabe 10.2]]
 +
 +
== Aufgabe 10.3 ==

Version vom 24. Juni 2010, 21:48 Uhr

Aufgabe 10.1

Definition V.9 : (noch mehr Senkrecht)

Eine Gerade \ g und eine Strecke \overline{AB} stehen senkrecht aufeinander, wenn die \ g und die Gerade \ AB senkrecht aufeinander stehen.

Ergänzen Sie:

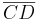Eine Strecke \ \overline{AB} und eine Strecke \ \overline{CD} stehen senkrecht aufeinander, wenn ... .
Eine Gerade \ g und eine Ebene \epsilon stehen senkrecht aueinander, wenn es in \epsilon ... .

Lösung von Aufgabe 10.1

Aufgabe 10.2

Beweisen Sie:

Satz V.5: (Existenz und Eindeutigkeit der Senkrechten zu einer Geraden auf einem Punkt dieser Geraden)

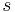Es sei \ g eine Gerade der Ebene \ \Epsilon. Ferner sei \ P ein Punkt auf \ g. In der Ebene \ \Epsilon gibt es genau eine Gerade \ s, die durch \ P geht und senkrecht auf \ g steht.

Lösung von Aufgabe 10.2

Aufgabe 10.3

Von „http://geometrie.zum.de/index.php?title=Übung_10&oldid=2331“