Lösung von Aufg. 6.3P (SoSe 13): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| Zeile 6: | Zeile 6: | ||
*** <math>M</math> ist konvex, wenn gilt: <math>\forall A, B \in M \wedge \overline{AB}\subset M.</math> | *** <math>M</math> ist konvex, wenn gilt: <math>\forall A, B \in M \wedge \overline{AB}\subset M.</math> | ||
****So sieht das in Formelschreibweise aus. Die Definition stimmt so noch nicht ganz. Kopiert die Aussage und verbessert diese dann. --[[Benutzer:Tutorin Anne|Tutorin Anne]] 19:45, 5. Jun. 2013 (CEST) | ****So sieht das in Formelschreibweise aus. Die Definition stimmt so noch nicht ganz. Kopiert die Aussage und verbessert diese dann. --[[Benutzer:Tutorin Anne|Tutorin Anne]] 19:45, 5. Jun. 2013 (CEST) | ||
| − | + | *****<math>M \Rightarrow \forall A,B.: A,B \in M \wedge \overline{AB} \in M</math>--[[Benutzer:Beencken|Beencken]] 19:37, 9. Jun. 2013 (CEST) | |
[[Kategorie:Einführung_P]] | [[Kategorie:Einführung_P]] | ||
Version vom 9. Juni 2013, 18:37 Uhr
Definieren Sie den Begriff: "konvexe Punktmenge" indem Sie die verbal formulierte Definition (siehe Wiki-Skript) in eine geeignete "Mengenschreibweise" übersetzen.
M ist konvex, wenn gilt: ...
- (M/ A ist Element M und B ist Element M) vereinigt mit der Strecke AB und Die Strecke AB ist Element M--Blumenkind 13:29, 1. Jun. 2013 (CEST)Blumenkind 13:29, 1.6.13
- Ich verstehe ehrlich nicht genau, was du damit sagen willst. So ist die Definition nicht richtig. Nutzt bitte auch die Formeln des Formeleditor (Symbol ganz links mit dem Summenzeichen).--Tutorin Anne 18:48, 2. Jun. 2013 (CEST)
- M ist konvex wenn gilt:
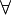A, B 
M und die Strecke AB ist eine echte Teilmenge von M.--Blumenkind 16:38, 3. Jun. 2013 (CEST)Blumenkind 16:38, 3. Juni
-
ist konvex, wenn gilt: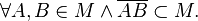 
- So sieht das in Formelschreibweise aus. Die Definition stimmt so noch nicht ganz. Kopiert die Aussage und verbessert diese dann. --Tutorin Anne 19:45, 5. Jun. 2013 (CEST)
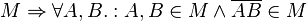--Beencken 19:37, 9. Jun. 2013 (CEST)
- So sieht das in Formelschreibweise aus. Die Definition stimmt so noch nicht ganz. Kopiert die Aussage und verbessert diese dann. --Tutorin Anne 19:45, 5. Jun. 2013 (CEST)
- M ist konvex wenn gilt:
- Ich verstehe ehrlich nicht genau, was du damit sagen willst. So ist die Definition nicht richtig. Nutzt bitte auch die Formeln des Formeleditor (Symbol ganz links mit dem Summenzeichen).--Tutorin Anne 18:48, 2. Jun. 2013 (CEST)
