|
|
| Zeile 8: |
Zeile 8: |
| | | | |
| | [[Kategorie:Einführung_P]] | | [[Kategorie:Einführung_P]] |
| − |
| |
| − | Ich probier es mal bin mir aber nicht sicher, ob es richtig ist.
| |
| − |
| |
| − | Da bei mir leider kein Geogebra funktioniert versuche ich es irgendwie mit Sätzen;-).
| |
| − |
| |
| − | Also:''' Eine Verkettung von vier Spiegelgeraden kann durch 2 Spiegelgeraden ersetzt werden. Falls sich die Geraden scheiden--> DREHUNG bzw. sind sie parallel--> VERSCHIEBUNG
| |
| − | '''''Kursiver Text''
| |
| − | * Zuerst habe ich eine Parallele zu c durch S gezogen und die gerade c` genannt mit c`II c und c´geschnitten b =(S).
| |
| − | * Ebenso wissen wir dass es eine weitere Gerade gibt mit d` zu c` c und d da diese drei Geraden parallel zueinander sind.
| |
| − | * Für '''d`gilt: Sc o Sd= Sc´o Sd´'''''
| |
| − | == Kursiver Text ==''
| |
| − |
| |
| − | <math>\Rightarrow</math> Sa o Sb o Sc o Sd
| |
| − |
| |
| − | * = Sa o Sb o Sc´o Sd´ ich habe die FORMEL die ich für d´geschrieben habe ersetzt einfach
| |
| − |
| |
| − | * = (Sa o Sb o Sc´) o Sd´ ich habe es in die Klammer zusammengefügt, da alle drei Geraden durch den selben Punkt S gehen. Bzw. zusammengefasst
| |
| − |
| |
| − | * = Sx o Sd´ (2) und Sx ist die neue Spiegelung
| |
| − |
| |
| − | * '''Daraus folgt das man eine Verkettung von 4 Geraden durch 2 ersetzen kann. --[[Benutzer:Blumenkind|Blumenkind]] 15:34, 12. Jul. 2013 (CEST)Blumenkind 15:32, 12. Juli
| |
| − | '''
| |
Version vom 12. Juli 2013, 15:46 Uhr
Gegeben sei ein Dreieck  und die Geraden a, b, c und d mit:
und die Geraden a, b, c und d mit: 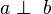 und
und 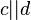 entsprechend der Skizze.
entsprechend der Skizze.
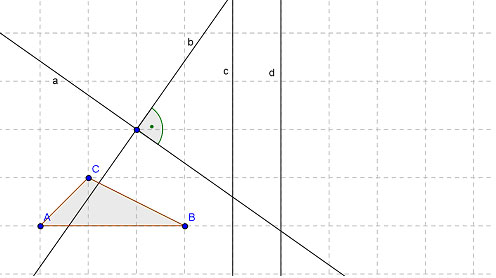
- Durch welche Abbildung kann die Verkettung der vier Geradenspiegelungen
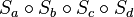 ersetzt werden (Begründen Sie Ihre Entscheidung)?
ersetzt werden (Begründen Sie Ihre Entscheidung)?
- Zeichnen Sie die Achsen der Ersatzabbildung in die Skizze oben ein. Hinweis: Sie dürfen das Gitter im Hintergrund als Orientierung nutzen.
- Konstruieren Sie oben in der Skizze das Bild des Dreiecks
 , das nach der Verkettung
, das nach der Verkettung 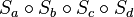 entsteht, mit Hilfe der Ersatzabbildung.
entsteht, mit Hilfe der Ersatzabbildung.
 und die Geraden a, b, c und d mit:
und die Geraden a, b, c und d mit: 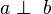 und
und 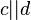 entsprechend der Skizze.
entsprechend der Skizze.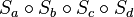 ersetzt werden (Begründen Sie Ihre Entscheidung)?
ersetzt werden (Begründen Sie Ihre Entscheidung)?
 , das nach der Verkettung
, das nach der Verkettung 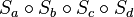 entsteht, mit Hilfe der Ersatzabbildung.
entsteht, mit Hilfe der Ersatzabbildung.

