Lösung von Aufgabe 11.4P (SoSe 13)
Aus Geometrie-Wiki
Gegeben sei ein Dreieck  und die Geraden a, b, c und d mit:
und die Geraden a, b, c und d mit: 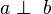 und
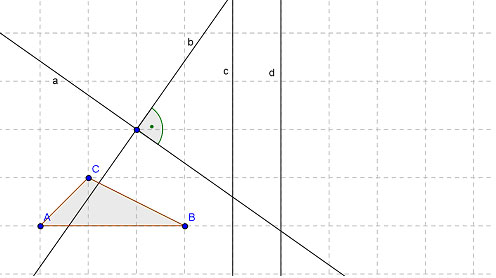
und 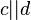 entsprechend der Skizze.
entsprechend der Skizze.
- Durch welche Abbildung kann die Verkettung der vier Geradenspiegelungen
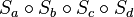 ersetzt werden (Begründen Sie Ihre Entscheidung)?
ersetzt werden (Begründen Sie Ihre Entscheidung)?
- Zeichnen Sie die Achsen der Ersatzabbildung in die Skizze oben ein. Hinweis: Sie dürfen das Gitter im Hintergrund als Orientierung nutzen.
- Konstruieren Sie oben in der Skizze das Bild des Dreiecks
 , das nach der Verkettung
, das nach der Verkettung 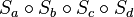 entsteht, mit Hilfe der Ersatzabbildung.
entsteht, mit Hilfe der Ersatzabbildung.
- zu 1) * Eine Verkettung von 4 Geradengleichungen kann immer als Verkettung von 2 Geradengleichungen dargestellt werden, mit b´II c und a`senkrecht b`, sowie gleichen Drehpunkt
--> EIGENSCHAFT DREHUNG
- Sa´ o Sb`o Sc` Sd`mit c`ist gleich b--> heben sich auch--> es bleibt nur noch a`und d` mit a´ist senkrecht zu d`
-->EIGENSCHAFT VERSCHIEBUNG
Warum heben die sich auf? --Tutorin Anne 18:02, 12. Jul. 2013 (CEST)
- --> Ersatzabbildung ist eine Punktspiegelung. Reicht es aus wenn ich nur sagen wie ich am Anfang gesagt habe, dass eine Verkettung von 4 Sg immer als Verkettung von 2 Sg dargestellt werden können? --Blumenkind 17:19, 12. Jul. 2013 (CEST)Blumenkind 17:08, 12. Juli
- Wenn du den Reduktionssatz (falls ihr den schon gelernt habt oder lernen werdet) als Begründung nutzt, ja. Damit hast du allerdings noch nicht ausgeschlossen, dass es auch eine Verschiebung sein könnte. Deshalb hast du richtig weitergemacht, indem du noch hergeleitet hast, warum es eine Punktspiegelung sein muss.--Tutorin Anne 18:02, 12. Jul. 2013 (CEST)
- Den Reduktionssatz haben wir noch nicht in der Vorlesung behandelt, aber auf der WIKI Seite stehen schon paar Sätzen über den Reduktionssatz. Ich gehe davon aus, dass wir es am Dienstag behandeln werden. Hätte es dann gereicht, wenn ich NICHT PUNKTSPIEGELUNG erwähne? --Blumenkind 18:35, 12. Jul. 2013 (CEST)Blumenkind 18:34, 12. Juli
- Nein, das hätte nicht gereicht, du sollst ja bei Aufgabe 1 zeigen, dass man diese Verkettung durch eine Punktspiegelung ersetzen kannst. Eine allgemeine Aussgae der Art "durch eine Verkettung von 2 Geraden" hilft einem ja noch nicht, um die Konstruktion durchzuführen.--Tutorin Anne 11:08, 16. Jul. 2013 (CEST)
- Den Reduktionssatz haben wir noch nicht in der Vorlesung behandelt, aber auf der WIKI Seite stehen schon paar Sätzen über den Reduktionssatz. Ich gehe davon aus, dass wir es am Dienstag behandeln werden. Hätte es dann gereicht, wenn ich NICHT PUNKTSPIEGELUNG erwähne? --Blumenkind 18:35, 12. Jul. 2013 (CEST)Blumenkind 18:34, 12. Juli
- Eine Frage dazu. müssen wir es auch beweisen können? Weil für die Verkettung von vier Geradenspiegelungen gibt es sechs Fälle? Wann hätte ich es beweisen müssen? Oder reichen die Sätze aus? --Blumenkind 14:57, 14. Jul. 2013 (CEST)Blumenkind 14:56, 14.Juli
- Begründen der Schritt, d.h. dass man Geradenlagen z.B. ändern darf, so lange bestimmt Kriterien erfüllt sind (Begründung: Eigenschaft der Punktspiegelung oder Verschiebung). Dass man zwei identische Spiegelgeraden, bei denen hintereinander gespiegelt wird weglassen kann, kann man ja auch begründen. Und das ist ähnlich einem Beweis. Das genügt absolut. Du musst die Reduktion ja für einen speziellen Fall (Verkettung der Punktspiegelung und der Verschiebung) zeigen. Alle Fälle auf einmal kann man mit dem Reduktionssatz reduzieren, ohne diese einzeln zu behandeln. Welche 6 Fälle überhaupt?--Tutorin Anne 11:08, 16. Jul. 2013 (CEST)