Lösung von Aufgabe 11.4P (SoSe 13): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| Zeile 7: | Zeile 7: | ||
#Konstruieren Sie oben in der Skizze das Bild des Dreiecks <math>\overline{ABC}</math>, das nach der Verkettung <math>S_{a}\circ S_{b}\circ S_{c}\circ S_{d} </math> entsteht, mit Hilfe der Ersatzabbildung.<br /> | #Konstruieren Sie oben in der Skizze das Bild des Dreiecks <math>\overline{ABC}</math>, das nach der Verkettung <math>S_{a}\circ S_{b}\circ S_{c}\circ S_{d} </math> entsteht, mit Hilfe der Ersatzabbildung.<br /> | ||
| + | ---- | ||
[[Kategorie:Einführung_P]] | [[Kategorie:Einführung_P]] | ||
| Zeile 12: | Zeile 13: | ||
--> '''EIGENSCHAFT DREHUNG''' | --> '''EIGENSCHAFT DREHUNG''' | ||
| − | + | * Sa´ o Sb`o Sc` Sd`mit c`ist gleich b--> heben sich auch--> es bleibt nur noch a`und d` mit a´ist senkrecht zu d` | |
| − | -->'''EIGENSCHAFT VERSCHIEBUNG' | + | -->'''EIGENSCHAFT VERSCHIEBUNG''' |
| − | + | Warum heben die sich auf? --[[Benutzer:Tutorin Anne|Tutorin Anne]] 18:02, 12. Jul. 2013 (CEST) | |
| − | + | * --> Ersatzabbildung ist eine Punktspiegelung. Reicht es aus wenn ich nur sagen wie ich am Anfang gesagt habe, dass eine Verkettung von 4 Sg immer als Verkettung von 2 Sg dargestellt werden können? --[[Benutzer:Blumenkind|Blumenkind]] 17:19, 12. Jul. 2013 (CEST)Blumenkind 17:08, 12. Juli | |
| − | --> Ersatzabbildung ist eine Punktspiegelung. Reicht es aus wenn ich nur sagen wie ich am Anfang gesagt habe, dass eine Verkettung von 4 Sg immer als Verkettung von 2 Sg dargestellt werden können? --[[Benutzer:Blumenkind|Blumenkind]] 17:19, 12. Jul. 2013 (CEST)Blumenkind 17:08, 12. Juli | + | ** Wenn du den Reduktionssatz (falls ihr den schon gelernt habt oder lernen werdet) als Begründung nutzt, ja. Damit hast du allerdings noch nicht ausgeschlossen, dass es auch eine Verschiebung sein könnte. Deshalb hast du richtig weitergemacht, indem du noch hergeleitet hast, warum es eine Punktspiegelung sein muss.--[[Benutzer:Tutorin Anne|Tutorin Anne]] 18:02, 12. Jul. 2013 (CEST) |
Version vom 12. Juli 2013, 17:02 Uhr
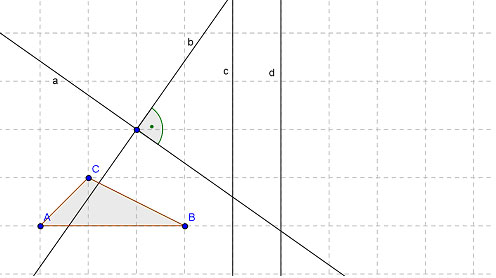
Gegeben sei ein Dreieck  und die Geraden a, b, c und d mit:
und die Geraden a, b, c und d mit: 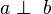 und
und 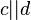 entsprechend der Skizze.
entsprechend der Skizze.
- Durch welche Abbildung kann die Verkettung der vier Geradenspiegelungen
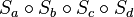 ersetzt werden (Begründen Sie Ihre Entscheidung)?
ersetzt werden (Begründen Sie Ihre Entscheidung)?
- Zeichnen Sie die Achsen der Ersatzabbildung in die Skizze oben ein. Hinweis: Sie dürfen das Gitter im Hintergrund als Orientierung nutzen.
- Konstruieren Sie oben in der Skizze das Bild des Dreiecks
 , das nach der Verkettung
, das nach der Verkettung 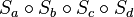 entsteht, mit Hilfe der Ersatzabbildung.
entsteht, mit Hilfe der Ersatzabbildung.
- zu 1) * Eine Verkettung von 4 Geradengleichungen kann immer als Verkettung von 2 Geradengleichungen dargestellt werden, mit b´II c und a`senkrecht b`, sowie gleichen Drehpunkt
--> EIGENSCHAFT DREHUNG
- Sa´ o Sb`o Sc` Sd`mit c`ist gleich b--> heben sich auch--> es bleibt nur noch a`und d` mit a´ist senkrecht zu d`
-->EIGENSCHAFT VERSCHIEBUNG
Warum heben die sich auf? --Tutorin Anne 18:02, 12. Jul. 2013 (CEST)
- --> Ersatzabbildung ist eine Punktspiegelung. Reicht es aus wenn ich nur sagen wie ich am Anfang gesagt habe, dass eine Verkettung von 4 Sg immer als Verkettung von 2 Sg dargestellt werden können? --Blumenkind 17:19, 12. Jul. 2013 (CEST)Blumenkind 17:08, 12. Juli
- Wenn du den Reduktionssatz (falls ihr den schon gelernt habt oder lernen werdet) als Begründung nutzt, ja. Damit hast du allerdings noch nicht ausgeschlossen, dass es auch eine Verschiebung sein könnte. Deshalb hast du richtig weitergemacht, indem du noch hergeleitet hast, warum es eine Punktspiegelung sein muss.--Tutorin Anne 18:02, 12. Jul. 2013 (CEST)