Übung 10: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Aufgabe 10.4) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 10.4) |
||
| (3 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 26: | Zeile 26: | ||
Warum ist die folgende Definition des Begriffs ''Winkelhalbierende'' nicht korrekt? | Warum ist die folgende Definition des Begriffs ''Winkelhalbierende'' nicht korrekt? | ||
| − | Die Halbgerade <math>\ SW^+</math> ist die Winkelhalbierende des Winkels <math>\angle ASB</math>, wenn <math>| \angle | + | Die Halbgerade <math>\ SW^+</math> ist die Winkelhalbierende des Winkels <math>\angle ASB</math>, wenn <math>| \angle ASW| = | \angle WSB |</math>. |
Eine Skizze genügt. | Eine Skizze genügt. | ||
| + | |||
| + | In der ersten Formulierung hatte ich anstelle von <math>\ W \ P</math> geschrieben. Dadurch war die Aufgabe natürlich, na ja Blödsinn.--[[Benutzer:*m.g.*|*m.g.*]] 21:44, 29. Jun. 2010 (UTC) | ||
| + | |||
| + | [[Lösung von Aufgabe 10.4]] | ||
| + | |||
| + | == Aufgabe 10.5 == | ||
| + | Beweisen Sie Satz VI.eineinhalb | ||
| + | |||
| + | [[Lösung von Aufgabe 10.5]] | ||
Aktuelle Version vom 29. Juni 2010, 22:44 Uhr
Inhaltsverzeichnis |
Aufgabe 10.1
Definition V.9 : (noch mehr Senkrecht)
- Eine Gerade
und eine Strecke 
stehen senkrecht aufeinander, wenn die und die Gerade 
senkrecht aufeinander stehen.
- Eine Gerade
Ergänzen Sie:
- Eine Strecke
und eine Strecke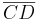 
stehen senkrecht aufeinander, wenn ... .
- Eine Strecke
- Eine Gerade und eine Ebene
stehen senkrecht aueinander, wenn es in ... .
- Eine Gerade
Aufgabe 10.2
Beweisen Sie:
Satz V.5: (Existenz und Eindeutigkeit der Senkrechten zu einer Geraden auf einem Punkt dieser Geraden)
- Es sei eine Gerade der Ebene
. Ferner sei 
ein Punkt auf . In der Ebene gibt es genau eine Gerade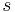 
, die durch geht und senkrecht auf steht.
- Es sei
Aufgabe 10.3
Formulieren Sie den Beweis von Satz VI.1, ohne das Tabellenbeweischema zu verwenden. Ferner mögen Sie angehalten sein, die mathematische Formelsprache zu vermeiden. Kurz und gut, ein Beweis mit eigenen Worten, grammatikalisch korrekt formuliert.
Aufgabe 10.4
Warum ist die folgende Definition des Begriffs Winkelhalbierende nicht korrekt?
Die Halbgerade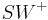 
ist die Winkelhalbierende des Winkels 
, wenn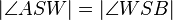 
.
Eine Skizze genügt.
In der ersten Formulierung hatte ich anstelle von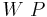 
geschrieben. Dadurch war die Aufgabe natürlich, na ja Blödsinn.--*m.g.* 21:44, 29. Jun. 2010 (UTC)
Aufgabe 10.5
Beweisen Sie Satz VI.eineinhalb
