Übung Aufgaben 10 (WS 16 17): Unterschied zwischen den Versionen

Version vom 3. Februar 2017, 19:55 Uhr

Aufgabe 10.1

Beweisen Sie die Halbgeradentreue der Geradenspiegelung. Nutzen Sie für den Beweis die Streckentreue der Geradenspiegelung und eine geeignete Definition des Begriffs Halbgerade.
Lösung von Aufgabe 10.1P (WS_16_17)

Aufgabe 10.2

Beweisen Sie die Geradentreue der Geradenspiegelung. Nutzen Sie für den Beweis die Halbgeradentreue der Geradenspiegelung.
Lösung von Aufgabe 10.2P (WS_16_17)

Aufgabe 10.3

Beweisen Sie die Winkeltreue der Geradenspiegelung. Nutzen Sie für den Beweis die Halbgeradentreue und die Eigenschaft der Geradenspiegelung winkelmaßerhaltend zu sein.
Lösung von Aufgabe 10.3P (WS_16_17)

Warum brauche ich hier die Winkelmaßerhaltung? In Schritt eins und zwei spiegele ich die beiden Halbgeraden des Ausgangswinkels, erhalte wiederum Halbgeraden aufgrund der Halbgeradentreue. Mit der Definition Winkel (Ein Winkel ist die Vereinigungsmenge zweier Strahlen mit gemeinsamen Anfangspunkt) habe ich doch eigentlich schon alles, was ich brauche?

Aufgabe 10.4

1. Was versteht man unter der Parallelentreue einer Geradenspiegelung?
2. Beweisen Sie die Parallelentreue einer Geradenspiegelung.
   

Lösung von Aufgabe 10.4P (WS_16_17)

Aufgabe 10.5

m sei Mittelsenkrechte der Strecke . Beweisen Sie durch Kontraposition: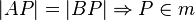
Tipp: Nutzen Sie den Satz von Pasch und die Dreiecksungleichung.
Hinweis: Die Umkehrung des hier zu beweisenden Satzes sei bereits bewiesen.
Lösung von Aufgabe 10.5P (WS_16_17)

Aufgaben Wintersemester 2016/2017

	Aufgaben	Auftrag der Woche	Quiz/Spiel der Woche	Zusatzaufgaben
Woche 1 (17.10.–23.10.)	Aufgaben 1	Auftrag der Woche 1	Quiz/Spiel der Woche 1	Zusatzaufgaben 1
Woche 2 (24.10.–30.10.)	Aufgaben 2	Auftrag der Woche 2	Quiz/Spiel der Woche 2	Zusatzaufgaben 2
Woche 3 (31.10.–6.11.)	Aufgaben 3	Auftrag der Woche 3	Quiz/Spiel der Woche 3	Zusatzaufgaben 3
Woche 4 (7.11.–13.10.)	Aufgaben 4	Auftrag der Woche 4	Quiz/Spiel der Woche 4	Zusatzaufgaben 4
Woche 5 (14.11.–20.11.)	Aufgaben 5	Auftrag der Woche 5	Quiz/Spiel der Woche 5	Zusatzaufgaben 5
Woche 6 (21.11.–27.11.)	Aufgaben 6	Auftrag der Woche 6	Quiz/Spiel der Woche 6	Zusatzaufgaben 6
Woche 7 (28.11.–4.12.)	Aufgaben 7	Auftrag der Woche 7	Quiz/Spiel der Woche 7	Zusatzaufgaben 7
Woche 8 (5.12.–11.12.)	Probeklausur
Woche 9 (12.12.–18.12.)	Aufgaben 9	Auftrag der Woche 9	Quiz/Spiel der Woche 9	Zusatzaufgaben 9
Woche 10 (19.12.–25.12.)	Aufgaben 10	Auftrag der Woche 10	Quiz/Spiel der Woche 10	Zusatzaufgaben 10
Woche 11 (9.1.–15.1.)	Aufgaben 11	Auftrag der Woche 11	Quiz/Spiel der Woche 11	Zusatzaufgaben 11
Woche 12 (16.1.–22.1.)	Aufgaben 12	Auftrag der Woche 12	Quiz/Spiel der Woche 12	Zusatzaufgaben 12