Übung Aufgaben 10 (WS 16 17): Unterschied zwischen den Versionen
(→Aufgabe 10.3) |
AlanTu (Diskussion | Beiträge) K (Bestimmter Artikel) |
||
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 15: | Zeile 15: | ||
Warum brauche ich hier die Winkelmaßerhaltung? In Schritt eins und zwei spiegele ich die beiden Halbgeraden des Ausgangswinkels, erhalte wiederum Halbgeraden aufgrund der Halbgeradentreue. Mit der Definition Winkel (Ein Winkel ist die Vereinigungsmenge zweier Strahlen mit gemeinsamen Anfangspunkt) habe ich doch eigentlich schon alles, was ich brauche? | Warum brauche ich hier die Winkelmaßerhaltung? In Schritt eins und zwei spiegele ich die beiden Halbgeraden des Ausgangswinkels, erhalte wiederum Halbgeraden aufgrund der Halbgeradentreue. Mit der Definition Winkel (Ein Winkel ist die Vereinigungsmenge zweier Strahlen mit gemeinsamen Anfangspunkt) habe ich doch eigentlich schon alles, was ich brauche? | ||
| + | : Dir fehlt aber dann bei deiner Begründung, dass der entstehende Winkel wieder genauso groß ist, wie der Ausgangswinkel. Es hätte ja auch sein können, dass <math>A'</math>, <math>B'</math> und <math>C'</math> zwar wieder einen Winkel ergeben, dieser aber kleiner oder größer ist, als der ursprüngliche Winkel vor der Spiegelung. --[[Benutzer:AlanTu|AlanTu]] ([[Benutzer Diskussion:AlanTu|Diskussion]]) 03:08, 4. Feb. 2017 (CET) | ||
| + | |||
| + | |||
| + | Hier noch kurz meine Überlegungen, wie Winkeltreue und Winkelmaßerhaltung differenziert werden können, das hat mir anfänglich nämlich auch Probleme bereitet: | ||
| + | * '''Winkeltreue''' bedeutet, dass ein Winkel (sprich zwei Halbgeraden mit gemeinsamem Ursprung) wieder auf einen Winkel mit selbem Winkelmaß abgebildet werden. | ||
| + | * '''Winkelmaßerhaltung''' bedeutet, dass zwei Strecken/Halbgeraden/Geraden <math>BA</math> bzw. <math>BA^+</math> und <math>DC</math> bzw. <math>DC^+</math> sowohl vorher als auch nachher im gleichen Winkel zueinander stehen (Erklärung, was das mathematisch heißt in den Unterpunkten) | ||
| + | :* Den Schnittpunkt der Geraden durch <math>A</math> und <math>B</math> mit der Geraden durch <math>C</math> und <math>D</math> nenne ich <math>S</math>, den Schnittpunkt der Spiegelgeraden nenne ich <math>S'</math> | ||
| + | :* Dann bedeutet Winkelmaßerhaltung, dass gilt <math>\angle ASC = \angle A'S'C'</math> | ||
| + | Winkeltreue ist also ein Spezialfall von Winkelmaßerhaltung, bei dem gilt <math>B=S=D</math>. | ||
| + | |||
| + | Die Abbildung ist winkeltreu <math>\Rightarrow</math> Die Abbildung ist winkelmaßerhaltend<br> | ||
| + | Die Abbildung ist winkeltreu <math>\nLeftarrow</math> Die Abbildung ist winkelmaßerhaltend --[[Benutzer:AlanTu|AlanTu]] ([[Benutzer Diskussion:AlanTu|Diskussion]]) 03:08, 4. Feb. 2017 (CET) | ||
==Aufgabe 10.4== | ==Aufgabe 10.4== | ||
Aktuelle Version vom 4. Februar 2017, 19:35 Uhr
Inhaltsverzeichnis |
Aufgabe 10.1
Beweisen Sie die Halbgeradentreue der Geradenspiegelung. Nutzen Sie für den Beweis die Streckentreue der Geradenspiegelung und eine geeignete Definition des Begriffs Halbgerade.
Lösung von Aufgabe 10.1P (WS_16_17)
Aufgabe 10.2
Beweisen Sie die Geradentreue der Geradenspiegelung. Nutzen Sie für den Beweis die Halbgeradentreue der Geradenspiegelung.
Lösung von Aufgabe 10.2P (WS_16_17)
Aufgabe 10.3
Beweisen Sie die Winkeltreue der Geradenspiegelung. Nutzen Sie für den Beweis die Halbgeradentreue und die Eigenschaft der Geradenspiegelung winkelmaßerhaltend zu sein.
Lösung von Aufgabe 10.3P (WS_16_17)
Warum brauche ich hier die Winkelmaßerhaltung? In Schritt eins und zwei spiegele ich die beiden Halbgeraden des Ausgangswinkels, erhalte wiederum Halbgeraden aufgrund der Halbgeradentreue. Mit der Definition Winkel (Ein Winkel ist die Vereinigungsmenge zweier Strahlen mit gemeinsamen Anfangspunkt) habe ich doch eigentlich schon alles, was ich brauche?
- Dir fehlt aber dann bei deiner Begründung, dass der entstehende Winkel wieder genauso groß ist, wie der Ausgangswinkel. Es hätte ja auch sein können, dass
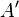 ,
, 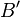 und
und 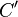 zwar wieder einen Winkel ergeben, dieser aber kleiner oder größer ist, als der ursprüngliche Winkel vor der Spiegelung. --AlanTu (Diskussion) 03:08, 4. Feb. 2017 (CET)
zwar wieder einen Winkel ergeben, dieser aber kleiner oder größer ist, als der ursprüngliche Winkel vor der Spiegelung. --AlanTu (Diskussion) 03:08, 4. Feb. 2017 (CET)
Hier noch kurz meine Überlegungen, wie Winkeltreue und Winkelmaßerhaltung differenziert werden können, das hat mir anfänglich nämlich auch Probleme bereitet:
- Winkeltreue bedeutet, dass ein Winkel (sprich zwei Halbgeraden mit gemeinsamem Ursprung) wieder auf einen Winkel mit selbem Winkelmaß abgebildet werden.
- Winkelmaßerhaltung bedeutet, dass zwei Strecken/Halbgeraden/Geraden
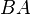 bzw.
bzw. 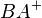 und
und 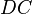 bzw.
bzw. 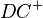 sowohl vorher als auch nachher im gleichen Winkel zueinander stehen (Erklärung, was das mathematisch heißt in den Unterpunkten)
sowohl vorher als auch nachher im gleichen Winkel zueinander stehen (Erklärung, was das mathematisch heißt in den Unterpunkten)
- Den Schnittpunkt der Geraden durch
 und
und  mit der Geraden durch
mit der Geraden durch  und
und  nenne ich
nenne ich  , den Schnittpunkt der Spiegelgeraden nenne ich
, den Schnittpunkt der Spiegelgeraden nenne ich 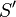
- Dann bedeutet Winkelmaßerhaltung, dass gilt
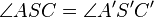
- Den Schnittpunkt der Geraden durch
Winkeltreue ist also ein Spezialfall von Winkelmaßerhaltung, bei dem gilt 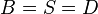 .
.
Die Abbildung ist winkeltreu  Die Abbildung ist winkelmaßerhaltend
Die Abbildung ist winkelmaßerhaltend
Die Abbildung ist winkeltreu 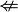 Die Abbildung ist winkelmaßerhaltend --AlanTu (Diskussion) 03:08, 4. Feb. 2017 (CET)
Die Abbildung ist winkelmaßerhaltend --AlanTu (Diskussion) 03:08, 4. Feb. 2017 (CET)
Aufgabe 10.4
- Was versteht man unter der Parallelentreue einer Geradenspiegelung?
- Beweisen Sie die Parallelentreue einer Geradenspiegelung.
Lösung von Aufgabe 10.4P (WS_16_17)
Aufgabe 10.5
m sei Mittelsenkrechte der Strecke  . Beweisen Sie durch Kontraposition:
. Beweisen Sie durch Kontraposition: 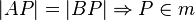
Tipp: Nutzen Sie den Satz von Pasch und die Dreiecksungleichung.
Hinweis: Die Umkehrung des hier zu beweisenden Satzes sei bereits bewiesen.
Lösung von Aufgabe 10.5P (WS_16_17)

