Das Lot von einem Punkt auf eine Gerade: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(→Definition IX.1: (Lot, Lotgerade, Lotfußpunkt)) |
|||
| Zeile 1: | Zeile 1: | ||
== Der Begriff des Lotes == | == Der Begriff des Lotes == | ||
| − | + | ||
===== Definition IX.1: (Lot, Lotgerade, Lotfußpunkt) ===== | ===== Definition IX.1: (Lot, Lotgerade, Lotfußpunkt) ===== | ||
:: Es sei <math>\ P</math> ein Punkt, der nicht zur Geraden <math>\ g</math> gehören möge. ...<br /> | :: Es sei <math>\ P</math> ein Punkt, der nicht zur Geraden <math>\ g</math> gehören möge. ...<br /> | ||
Version vom 12. Juli 2010, 23:49 Uhr
Inhaltsverzeichnis |
Der Begriff des Lotes
Definition IX.1: (Lot, Lotgerade, Lotfußpunkt)
- Es sei
 ein Punkt, der nicht zur Geraden
ein Punkt, der nicht zur Geraden  gehören möge. ...
gehören möge. ...
- ...Die Gerade
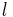 , die senkrecht auf
, die senkrecht auf  steht und durch den Punkt
steht und durch den Punkt  geht heißt Lotgerade von
geht heißt Lotgerade von  auf
auf  . Der Schnittpunkt
. Der Schnittpunkt  von
von 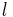 mit
mit  , heißt Lotfußpunkt des Lotes von
, heißt Lotfußpunkt des Lotes von  auf
auf  . Unter dem Lot von
. Unter dem Lot von  auf
auf  , versteht man die Strecke
, versteht man die Strecke 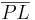 . --Löwenzahn 16:01, 9. Jul. 2010 (UTC)
. --Löwenzahn 16:01, 9. Jul. 2010 (UTC)
- Es sei
Definition IX.2: (Abstand eines Punktes zu einer Geraden)
- Es sei
 ein Punkt außerhalb von
ein Punkt außerhalb von  . Der Abstand von
. Der Abstand von  zu
zu  ist ...
ist ...
- ... die Länge der Lotes
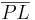 von
von  auf
auf  . --Löwenzahn 16:06, 9. Jul. 2010 (UTC)
. --Löwenzahn 16:06, 9. Jul. 2010 (UTC)
- Es sei
Existenz und Eindeutigkeit des Lotes
Satz XI.1: (Existenz und Eindeutigkeit des Lotes)
- Zu jedem Punkt
 außerhalb einer Geraden
außerhalb einer Geraden  gibt es genau ein Lot von
gibt es genau ein Lot von  auf
auf  .
.
- Zu jedem Punkt

