Auftrag der Woche 3: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) |
*m.g.* (Diskussion | Beiträge) |
||
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
# Unter <math>\mathcal{M}</math> wollen wir die Menge aller Mengen verstehen. Wir teilen <math>\mathcal{M}</math> nun in unendlich viele Teilmengen ein:<math>\varnothing , M_1, M_2, M_3, M_4, ... , M_n, ... </math>. Dabei verstehen wir unter <math>\varnothing </math> die leere Menge, unter <math>M_1</math> die Menge aller Mengen mit genau einem Element, unter <math>M_2</math> die Menge aller Mengen mit genau zwei Elementen, unter <math>M_n</math> die Menge aller Mengen mit genau <math>n</math> Elementen etc. . | # Unter <math>\mathcal{M}</math> wollen wir die Menge aller Mengen verstehen. Wir teilen <math>\mathcal{M}</math> nun in unendlich viele Teilmengen ein:<math>\varnothing , M_1, M_2, M_3, M_4, ... , M_n, ... </math>. Dabei verstehen wir unter <math>\varnothing </math> die leere Menge, unter <math>M_1</math> die Menge aller Mengen mit genau einem Element, unter <math>M_2</math> die Menge aller Mengen mit genau zwei Elementen, unter <math>M_n</math> die Menge aller Mengen mit genau <math>n</math> Elementen etc. . | ||
| − | # Element | + | # Unter <math>\mathcal{M}</math> wollen wir die Menge aller Mengen verstehen. Wir teilen <math>\mathcal{M}</math> nun in unendlich viele Teilmengen ein:<math>M_0 , M_1, M_2, M_3, M_4, ... , M_n, ... </math>. Dabei verstehen wir unter <math>M_0 </math> die Menge, die die leere Menge enthält. Unter <math>M_1</math> verstehen wir die Menge aller Mengen mit genau einem Element, unter <math>M_2</math> die Menge aller Mengen mit genau zwei Elementen, unter <math>M_n</math> die Menge aller Mengen mit genau <math>n</math> Elementen etc. . |
| − | + | ||
Aktuelle Version vom 29. April 2010, 21:31 Uhr
Diskutieren Sie, ob es sich in den folgenden beiden Fällen um Klasseneinteilungen handelt:
- Unter
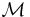 wollen wir die Menge aller Mengen verstehen. Wir teilen
wollen wir die Menge aller Mengen verstehen. Wir teilen 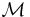 nun in unendlich viele Teilmengen ein:
nun in unendlich viele Teilmengen ein: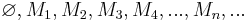 . Dabei verstehen wir unter
. Dabei verstehen wir unter 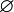 die leere Menge, unter
die leere Menge, unter 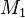 die Menge aller Mengen mit genau einem Element, unter
die Menge aller Mengen mit genau einem Element, unter  die Menge aller Mengen mit genau zwei Elementen, unter
die Menge aller Mengen mit genau zwei Elementen, unter 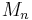 die Menge aller Mengen mit genau
die Menge aller Mengen mit genau  Elementen etc. .
Elementen etc. .
- Unter
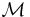 wollen wir die Menge aller Mengen verstehen. Wir teilen
wollen wir die Menge aller Mengen verstehen. Wir teilen 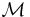 nun in unendlich viele Teilmengen ein:
nun in unendlich viele Teilmengen ein: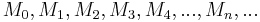 . Dabei verstehen wir unter
. Dabei verstehen wir unter 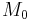 die Menge, die die leere Menge enthält. Unter
die Menge, die die leere Menge enthält. Unter 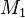 verstehen wir die Menge aller Mengen mit genau einem Element, unter
verstehen wir die Menge aller Mengen mit genau einem Element, unter  die Menge aller Mengen mit genau zwei Elementen, unter
die Menge aller Mengen mit genau zwei Elementen, unter 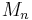 die Menge aller Mengen mit genau
die Menge aller Mengen mit genau  Elementen etc. .
Elementen etc. .

