Lösung von Aufgabe 3.4 (WS 11/12): Unterschied zwischen den Versionen
RicRic (Diskussion | Beiträge) |
RicRic (Diskussion | Beiträge) |
||
| Zeile 15: | Zeile 15: | ||
<math>\angle p,a = \angle q,b</math> = 90° | <math>\angle p,a = \angle q,b</math> = 90° | ||
| − | <math>\overline{SA} = \overline{ | + | <math>\overline{SA} = \overline{SA}</math> |
Behauptung1: | Behauptung1: | ||
| Zeile 36: | Zeile 36: | ||
| + | Voraussetzung: | ||
| + | |||
| + | <math>\angle w,p = \angle w,q</math> | ||
| + | |||
| + | <math>\angle p,a = \angle q,b</math> = 90° | ||
| + | |||
| + | <math>\overline{SA} = \overline{SA}</math> | ||
| + | |||
| + | <math>\left| Ap \right| =a</math> | ||
| + | |||
| + | <math>\left| Aq \right| =b</math> | ||
| Zeile 41: | Zeile 52: | ||
<math>\forall A :\left| Ap \right| = \left| Aq \right| \Leftrightarrow A\in w</math> | <math>\forall A :\left| Ap \right| = \left| Aq \right| \Leftrightarrow A\in w</math> | ||
| + | |||
| + | Annahme: | ||
| + | |||
| + | <math>\exists A :\left| Ap \right| = \left| Aq \right| \Leftrightarrow A\not\in w</math> | ||
| + | |||
| + | Beweis2: | ||
| + | |||
| + | <math>A\not\in w \wedge a =b \wedge \overline{AS} = \overline{AS} \wedge \angle b,q \angle a,p \Rightarrow triangle SAB \tilde {=} \triangle SCA</math> SsW Dreicke die an zwei Seitenlängen und dem Winkel der, der längeren Seite gegenüberliegt übereinstimen sind konguent. | ||
| + | |||
| + | <math>\triangle SAB \tilde {=} \triangle SCA \Rightarrow \angle b,q =\angle a,p \wedge \angle a,w =\angle b,w \wedge \angle p,w = \angle q,w</math> Da an konguenten Dreiecken alle Winkel konguent sind. | ||
| + | |||
| + | <math>\angle p,w = \angle q,w \Rightarrow A\in w\lightning</math> Wiederspruch A muss also Element w sein. | ||
| + | |||
| + | |||
--[[Benutzer:RicRic|RicRic]] | --[[Benutzer:RicRic|RicRic]] | ||
Version vom 1. November 2011, 13:31 Uhr
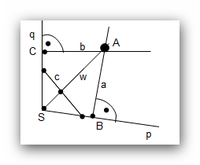
Beweisen Sie auf der Grundlage der Definition aus Aufgabe 3.3:
Die Winkelhalbierende eines Winkels ist die Menge aller Punkte, die im Inneren des Winkels liegen und deren Abstände von den beiden Schenkeln des Winkels jeweils gleich sind.
Anmerkung:
- Der Abstand eines Punktes P auf eine Gerade g ist die Länge des Lotes von P auf g.
- Der Beweis geht in zwei Schritten: Sie müssen erstens zeigen, dass jeder Punkt der Winkelhalbierenden (entspr. Def. Aufg. 3.3) von den beiden Schenkeln den gleichen Abstand hat und zweitens, dass jeder Punkt, der von den beiden Schenkeln den gleichen Abstand hat und im Inneren des Winkels liegt, zur Winkelhalbierenden (entspr. Def. Aufg. 3.3) gehört.
- Die Beweise lassen sich mit Hilfe der Kongruenzsätze führen, die Sie aus der Schule bereits kennen sollten.
Voraussetzung:
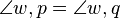
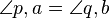= 90°
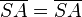
Behauptung1:
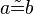
Beweis:
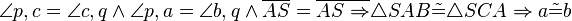Kongruenzsatz WSW
- Durch die Unterstützung mit dem Bild werden die Bezeichnungen zwar deutlich, aber warum wird der Strahl p mit dem Strahl c ersetzt? Ich denke, dass dies vllt. zu Verwirrungen führen kann.
- Wird hier wirklich der Kongruenzsatz WSW benutzt?
- Die Begründungen für die einzelnen Schritte sind hier zwar relativ naheliegend, sollten aber trotzdem, der Vollständigheit halber, genannt werden. --Tutor Andreas 15:02, 31. Okt. 2011 (CET)
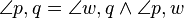
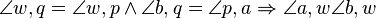Da wenn zwei Winkel in einem Dreieck feststehen, steht der dritte auch fest, da die Summer allder drei Winkel in Dreieck immer 180 Grad ist.
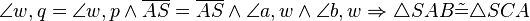WSW Winkel Seite Winkel sind konguent also sind die Dreicke konguent.
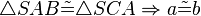Wenn die Dreiecke konguent sind müssen die Strecken ebenfalls konguent sein. --RicRic
Voraussetzung:
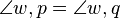
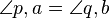= 90°
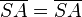
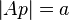
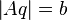
Behauptung2:
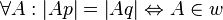
Annahme:
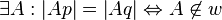
Beweis2:
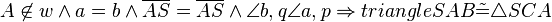SsW Dreicke die an zwei Seitenlängen und dem Winkel der, der längeren Seite gegenüberliegt übereinstimen sind konguent.
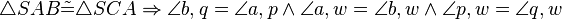Da an konguenten Dreiecken alle Winkel konguent sind.
Fehler beim Parsen(Unbekannte Funktion „\lightning“): \angle p,w = \angle q,w \Rightarrow A\in w\lightning
Wiederspruch A muss also Element w sein.
--RicRic
