Lösung von Aufg. 9.5 (WS 11/12): Unterschied zwischen den Versionen
RicRic (Diskussion | Beiträge) |
|||
| Zeile 6: | Zeile 6: | ||
a. Eine Konkave Punktmenge ist eine Menge von Punkten für die gilt, dass beim Verbinden aller Punkte mit allen Punkten, sich auf irgendeiner dieser durch das Verbinden erhaltenen Strecken, sich wenigstens ein Punkt findet, welcher nicht zu der Punktmenge gehört.--[[Benutzer:RicRic|RicRic]] 18:21, 6. Dez. 2011 (CET)<br /> | a. Eine Konkave Punktmenge ist eine Menge von Punkten für die gilt, dass beim Verbinden aller Punkte mit allen Punkten, sich auf irgendeiner dieser durch das Verbinden erhaltenen Strecken, sich wenigstens ein Punkt findet, welcher nicht zu der Punktmenge gehört.--[[Benutzer:RicRic|RicRic]] 18:21, 6. Dez. 2011 (CET)<br /> | ||
| + | Ich versuche es mal formal: <math>\forall P, Q \in M: \exists S\in \overline{PQ} \ \Rightarrow S\not\in M</math> --[[Benutzer:Todah raba|Todah raba]] 17:37, 7. Dez. 2011 (CET) | ||
b. | b. | ||
[[Category:Einführung_Geometrie]] | [[Category:Einführung_Geometrie]] | ||
Version vom 7. Dezember 2011, 17:37 Uhr
a) Definieren Sie den Begriff: "Konkave Punktmenge" ohne den Begriff "konvex" zu gebrauchen.
b) Begründen Sie, dass der Schnitt einer offenen Halbebene E mit einer Halbgeraden, die zwei Punkte mit E gemeinsam hat, auf jeden Fall eine konvexe Punktmenge ist.
c) Zeigen Sie an einem Beispiel, dass die Vereinigungsmenge des Inneren zweier Drachenvierecke, die keine Rauten sind, konkav sein kann.
a. Eine Konkave Punktmenge ist eine Menge von Punkten für die gilt, dass beim Verbinden aller Punkte mit allen Punkten, sich auf irgendeiner dieser durch das Verbinden erhaltenen Strecken, sich wenigstens ein Punkt findet, welcher nicht zu der Punktmenge gehört.--RicRic 18:21, 6. Dez. 2011 (CET)
Ich versuche es mal formal: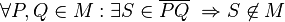 
--Todah raba 17:37, 7. Dez. 2011 (CET)
b.
