Lösung von Aufg. 9.5 (WS 11/12)

a) Definieren Sie den Begriff: "Konkave Punktmenge" ohne den Begriff "konvex" zu gebrauchen.

b) Begründen Sie, dass der Schnitt einer offenen Halbebene E mit einer Halbgeraden, die zwei Punkte mit E gemeinsam hat, auf jeden Fall eine konvexe Punktmenge ist.

c) Zeigen Sie an einem Beispiel, dass die Vereinigungsmenge des Inneren zweier Drachenvierecke, die keine Rauten sind, konkav sein kann.

a. Eine Konkave Punktmenge ist eine Menge von Punkten für die gilt, dass beim Verbinden aller Punkte mit allen Punkten, sich auf irgendeiner dieser durch das Verbinden erhaltenen Strecken, sich wenigstens ein Punkt findet, welcher nicht zu der Punktmenge gehört.--RicRic 18:21, 6. Dez. 2011 (CET)
Ich versuche es mal formal: Eine Menge M von Punkten heißt konkav wenn: 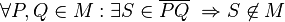$\forall P, Q \in M: \exists S\in \overline{PQ} \ \Rightarrow S\not\in M$ --Todah raba 17:37, 7. Dez. 2011 (CET)
Gute Idee, aber ich denke an einer Stelle ist ein kleiner Fehler, ich denke es muss heißen: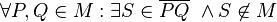$\forall P, Q \in M: \exists S\in \overline{PQ} \ \wedge S\not\in M$--RicRic 21:55, 8. Dez. 2011 (CET)

Mmh.... muss das denn wirklich 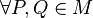$\forall P, Q \in M$ gelten? --Spannagel 13:27, 10. Dez. 2011 (CET)

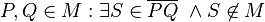$P, Q \in M: \exists S\in \overline{PQ} \ \wedge S\not\in M$Stimmt es reicht ja wenn in Punkt sich irgendwo außerhalb findet--RicRic 16:03, 11. Dez. 2011 (CET)

• ich würde das "es exisitert" auch ganz an Anfang stellen (M heißt konkav, wenn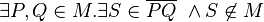$\exists P, Q \in M. \exists S\in \overline{PQ} \ \wedge S\not\in M$), so dass es gesprochen heißt: Eine Menge M heißt konkav, wenn zwei Punkte P und Q der Menge M existieren, für die gilt, dass ein Punkt S der Strecke PQ nicht zur Menge M gehört. Herr Spannagel, ist dies nötig?--Tutorin Anne 15:33, 14. Dez. 2011 (CET)

b. Wenn von einer Halbgeraden nur zwei Punke in der offnen Halbebenen liegen, dann bedeutet dies, dass der Ursprungspunkt und ein weiterer Punkt nähmlich der neben dem Ursprungspunkt in dieser offenen Halbebenen liegen. Der nächste also der dritte Punkt der Halbgeraden liegt dann bereits auf Geraden welche die Halbebene erzeugt. Schneide ich jetzt die offene Halbebene mit diesem Strahl erhalte die Punktmenge von zwei Punkten die nebeneinander liegen. Zwei Punkte die nebeneinander liegen haben keinen Punkt zwischen sich und sind somit immer konvex. Wären mehr Punkte in der Schnittmenge, wäre die Vorraussetzung verletzt, zwei Punkte die nicht nebeneinander liegen kommen auf Grund der Def. von der Halbgeraden nicht in Frage. --RicRic 22:01, 8. Dez. 2011 (CET)

• Ich finde die Aussage "Zwischen zwei Punkten, die nebeneinander liegen, liegt kein Punkt" in dieser Argumentation etwas fraglich, denn zu jeder reellen Zahl findet man auf einer Geraden einen Punkt... (Axiom vom Lineal) und da es zwischen zwei reellen Zahlen immer unendlich viele Zahlen gibt, muss es auch zwischen zwei Punkten unendlich viele Punkte geben... klingt doch logisch oder :D --Tutor Andreas 18:40, 14. Dez. 2011 (CET)

Ein Hinweis: In der Aufgabenstellung steht, dass sie zwei Punkte gemeinsam haben - nicht genau zwei. --Spannagel 13:30, 10. Dez. 2011 (CET)

c.

--RicRic 22:16, 8. Dez. 2011 (CET)

• b) hätte ich anders begründet.Der Ursprungspunkt der Geraden Halbgeraden muss ja nicht unbedingt in der Halbebene liegen. Wir haben ja das Inzidenzaxiom I/5, welches besagt, dass wenn zwei Punkte einer Geraden g in einer Ebene E liegen, g zu E gehört.

Wir haben es hier allerdings mit einer Halbgeraden und einer offenen Halbebene zu tun, anschaulich ist das aber ganz ähnlich. Zwischen zwei beliebigen Punkten, die in der Schnittmenge enthalten sind, gibt es demnach keine Punkte, die außerhalb der Ebene liegen. Der Ursprungspunkt könnte jedoch trotzdem außerhalb der Halbebene liegen.--Miriam 13:12, 10. Dez. 2011 (CET)

• Ich denke, wenn man das ganze in dieser Art begründen will, dann muss man zwei Fälle unterscheiden.

A und B seien die Punkte, die sowohl zu E als auch zum Strahl g gehören.

1. Der Strahl g schneidet die Trägergerade der offenen Halbebene E.
2. Der Strahl g schneidet die Trägergerade der offenen Halbebene E nicht.

Im Folgenden würde ich dann untersuchen, wie die Schnittmengen aussehen und dann mit Hilfe des Axioms von Pasch begründen. Dies ist, denke ich, nicht ganz einfach und der Vorschlag von Von Tutorin Anne ist weit einfacher. Falls es doch jemand versuchen möchte, nur zu... ich schaue es mir an und helfe auch ein bischen :D --Tutor Andreas 19:12, 14. Dez. 2011 (CET)

• • Diese Aussage lässt sich auch ganz anders begründen. Man könnte den Satz "Der Schnitt zweier konvexer Punktmengen ist konvex." nutzen. Wie könnte man dann argumentieren?--Tutorin Anne 15:33, 14. Dez. 2011 (CET)

• a) es seien zwei verschieden Punkte A und B Element der Punktmenge M.

 Wenn die Stecke AB nich vollständig in M liegt, so ist M eine konkave Punktmenge. --Schmarn 10:54, 14. Dez. 2011 (CET)

• diese Aussage ist so nicht richtig. Es könnte ja sein, man wählt zwei Punkte A und B und stellt fest, dass die Strecke $\overline{AB}$ enthalten ist. Trotzdem könnte es sein, dass die Menge konkav ist (an einer anderen Stelle). Durch eine kleine Änderung der Formulierung lässt sich dieses Problem beheben. Welche?--Tutorin Anne 15:33, 14. Dez. 2011 (CET)