Lösung von Aufg. 13.2 (WS 11/12): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
 
(4 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt)
Zeile 2: Zeile 2:
  
 
Kann man, um diese Implikation zu beweisen, das Parallelnaxiom verwenden?
 
Kann man, um diese Implikation zu beweisen, das Parallelnaxiom verwenden?
−
* Mann kann es in der absoluten Geometrie beweisen. D.h. ohne Parallelaxiom. --[[Benutzer:RicRic|RicRic]] 07:53, 23. Jan. 2012 (CET)
+
* Mann kann es in der absoluten Geometrie beweisen. D.h. ohne Parallelaxiom. --[[Benutzer:RicRic|RicRic]] 07:53, 23. Jan. 2012 (CET
 +
 
 +
<br />
 +
Vor: P, g, P <math>\not\in</math> g <br />
 +
Beh: P <math>\in</math> h <math>\wedge</math> <math>h\|| g</math>
 +
 
 +
 
 +
{| class="wikitable "
 +
! Beweisschritt
 +
! Begründung
 +
|-
 +
| 1) <math>\exists</math> R, L : R,L <math>\in</math> g
 +
| Axiom I.2
 +
|-
 +
| 2) <math>\exists</math> l: P, L <math>\in</math> l <math>\wedge</math> <math>\ l \perp \ g</math> <math>\wedge</math> <math>\ l \cap g</math> = {L}
 +
| Ex. und Eind. Lot, (1)
 +
|-
 +
| 3) <math>\exists</math> Q: Q <math>\in</math> gP<sup>+</sup> <math>\wedge</math> <math>Q \neq P</math>
 +
| Definition Halbebene
 +
|-
 +
| 4) <math>\exists</math> PA<sup>+</sup>: <math>\angle APL</math> = 90 <math>\wedge</math> PA<sup>+</sup> Teilmenge von lQ<sup>+</sup>
 +
| Axiom IV.2, (2), (3)
 +
|-
 +
| 5) <math>\angle APL</math> <math>\tilde {=}</math>  <math>\angle RLP</math>
 +
|(2), (4)
 +
|-
 +
| 6) <math>h\|| g</math>
 +
| (5), Umkehrung Wechselwinkelsatz
 +
|-
 +
| q.e.d.
 +
|
 +
|}
 +
--[[Benutzer:Adores|Adores]] 01:36, 24. Jan. 2012 (CET)
 +
 
 +
Gut! Allerdings würde eine Skizze das Nachvollziehen wesentlich vereinfachen! <br />So ist mir allerdings aufgefallen, dass Schritt (6) nicht immer geht, da die Winkel <math>\angle APL</math> und <math>\angle RLP</math> nicht immer Wechselwinkel sind! Stimmt's?<br /> Das lässt sich durch eine Skizze einfach darstellen!--[[Benutzer:Tutorin Anne|Tutorin Anne]] 13:13, 25. Jan. 2012 (CET)
  
 
[[Category:Einführung_Geometrie]]
 
[[Category:Einführung_Geometrie]]
 +
 +
{| class="wikitable sortable"
 +
!Schritt!!Begründung
 +
|-
 +
| 1. es existiert eine senkrechte f zu g || ( ex.und ein. senkrechten)
 +
|-
 +
| 2. <math>alpha=90</math> || (1), (def. senkrecht)
 +
|-
 +
| 3. es existiert das Lot m von P auf g || (Ex. und EInd. Lot)
 +
|-
 +
| 4. <math>beta=90</math>  || (3),( Def. Lot)
 +
|-
 +
| 5. <math>alpha=beta</math>  || (2), (4), (Def. Stufenwinkel)
 +
|-
 +
| 6. <math>hparallelg</math> || (5),(Umkehrung Stufenwinkelsatz)
 +
 +
|}
 +
q.e.d.
 +
--[[Benutzer:Celebino|Celebino]] 15:55, 26. Jan. 2012 (CET)<br />
 +
Celebino, ich habe deinen Beweis in die Tabelle eingefügt. Allerdings kann ich ihn nicht nachvollziehen. Welche Winkel meinst du denn mit alpha und beta. Und wo soll f liegen? Der Beweis muss schon ausführlicher sein. Eine Skizze (auch eingescannt oder aus Paint) würde helfen deinen Ansatz zu verstehen.--[[Benutzer:Tutorin Anne|Tutorin Anne]] 17:17, 29. Jan. 2012 (CET)

Aktuelle Version vom 29. Januar 2012, 17:17 Uhr

Beweisen Sie: Wenn \ P ein Punkt außerhalb der Geraden \ g ist, dann gibt es eine Gerade \ h, die durch \ P geht und parellel zu \ g ist.

Kann man, um diese Implikation zu beweisen, das Parallelnaxiom verwenden?

  • Mann kann es in der absoluten Geometrie beweisen. D.h. ohne Parallelaxiom. --RicRic 07:53, 23. Jan. 2012 (CET


Vor: P, g, P 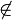\not\in g
Beh: P \in h \wedge h\|| g


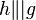
Beweisschritt Begründung
1) \exists R, L : R,L \in g Axiom I.2
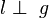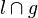2) \exists l: P, L \in l \wedge \ l \perp \ g \wedge \ l \cap g = {L} Ex. und Eind. Lot, (1)
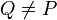
3) \exists Q: Q \in gP+ \wedge Q \neq P Definition Halbebene
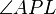4) \exists PA+: \angle APL = 90 \wedge PA+ Teilmenge von lQ+ Axiom IV.2, (2), (3)
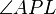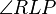
5) \angle APL \tilde {=} \angle RLP (2), (4)
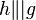
6) h\|| g (5), Umkehrung Wechselwinkelsatz
q.e.d.

--Adores 01:36, 24. Jan. 2012 (CET)

Gut! Allerdings würde eine Skizze das Nachvollziehen wesentlich vereinfachen!
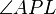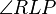So ist mir allerdings aufgefallen, dass Schritt (6) nicht immer geht, da die Winkel \angle APL und \angle RLP nicht immer Wechselwinkel sind! Stimmt's?
Das lässt sich durch eine Skizze einfach darstellen!--Tutorin Anne 13:13, 25. Jan. 2012 (CET)

Schritt Begründung
1. es existiert eine senkrechte f zu g ( ex.und ein. senkrechten)
2. 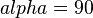alpha=90 (1), (def. senkrecht)
3. es existiert das Lot m von P auf g (Ex. und EInd. Lot)
4. 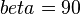beta=90 (3),( Def. Lot)
5. 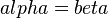alpha=beta (2), (4), (Def. Stufenwinkel)
6. 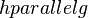hparallelg (5),(Umkehrung Stufenwinkelsatz)

q.e.d. --Celebino 15:55, 26. Jan. 2012 (CET)
Celebino, ich habe deinen Beweis in die Tabelle eingefügt. Allerdings kann ich ihn nicht nachvollziehen. Welche Winkel meinst du denn mit alpha und beta. Und wo soll f liegen? Der Beweis muss schon ausführlicher sein. Eine Skizze (auch eingescannt oder aus Paint) würde helfen deinen Ansatz zu verstehen.--Tutorin Anne 17:17, 29. Jan. 2012 (CET)

Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufg._13.2_(WS_11/12)&oldid=10915“