Übung Aufgaben 2 (SoSe 12): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
 
(3 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt)
Zeile 1: Zeile 1:
 +
=Aufgaben zu Definitionen=
 +
 +
==Aufgabe 3.1==
 +
Unter einer Konventionaldefinition versteht man eine Definition, die in der Form "Wenn-Dann" formuliert wurde.<br />
 +
Geben Sie zwei prinzipiell verschiedene Konventionaldefinitionen des Begriffs ''Mittelsenkrechte'' einer Strecke an.<br />
 +
[[Lösung von Aufgabe 3.1_S (SoSe_12)]]
 +
 +
 
=Aufgaben zu Sätzen und Beweisen=
 
=Aufgaben zu Sätzen und Beweisen=
−
==Aufgabe 2.1==
 
−
Der Basiswinkelsatz lautet: Im gleichschenkligen Dreieck sind die Basiswinkel kongruent zueinander.<br />
 
−
a) Wie lautet die Umkehrung des Basiswinkelsatzes?<br />
 
−
b) Fassen Sie den Basiswinkelsatz und seine Umkehrung zu einem Satz zusammen (Kriterium).
 
−
<br />
 
−
[[Lösung von Aufgabe 2.1_S (SoSe_12)]]
 
  
−
==Aufgabe 2.2==
+
==Aufgabe 3.2==
 +
Wir gehen von folgender Implikation aus: Wenn zwei Geraden g und h nicht identisch sind, dann haben sie höchstens einen Punkt gemeinsam.<br />
 +
a) Wie lautet die Kontraposition dieser Implikation?<br />
 +
b) Wie lautet die Annahme, wenn Sie diese Implikation durch einen Widerspruch beweisen möchten?<br />
 +
[[Lösung von Aufgabe 3.2_S (SoSe_12)]]
 +
 
 +
==Aufgabe 3.3==
 
'''Satz: In einem Dreieck <math>\overline{ABC} </math> mit  |AC|< |BC|  < |AB|  sind die Winkel α und β nicht kongruent zueinander.
 
'''Satz: In einem Dreieck <math>\overline{ABC} </math> mit  |AC|< |BC|  < |AB|  sind die Winkel α und β nicht kongruent zueinander.
 
'''<br /><br />
 
'''<br /><br />
Zeile 25: Zeile 33:
 
b) '''Beweisen Sie den Satz indirekt mit Widerspruch.'''<br />
 
b) '''Beweisen Sie den Satz indirekt mit Widerspruch.'''<br />
  
−
[[Lösung von Aufgabe 2.2_S (SoSe_12)]]
+
[[Lösung von Aufgabe 3.3_S (SoSe_12)]]
  
−
==Aufgabe 2.3==
+
==Aufgabe 3.4==
−
a) Wie lautet der Stufenwinkelsatz? (schauen Sie bei Bedarf in Schulbüchern nach).<br />
+
−
b) Es seien ''a'' und ''b'' zwei nichtidentische Geraden, die durch eine dritte Gerade ''c'' jeweils in genau einem Punkt ''S'' geschnitten werden. Bei diesem Schnitt entstehen die Stufenwinkel <math>\alpha </math> und <math>\beta </math>. Welche der folgenden Aussagen repräsentiert den Stufenwinkelsatz bzw. ist eine zu diesem Satz äuivalente Aussage (Begründen Sie jeweils)?<br />
+
−
#<math>\ a \ \|| \ b \Rightarrow \alpha \tilde {=} \beta </math>
+
−
#<math>\alpha \tilde {=} \beta \Rightarrow \ a \ \|| \ b </math>
+
−
#<math>\|\alpha \|\not= \| \beta \| \Rightarrow \exists S: S \in a \wedge S \in b </math>
+
−
#<math>\ a \ \|| \ b \Leftrightarrow \alpha \tilde {=} \beta </math>
+
−
[[Lösung von Aufgabe 2.3_S (SoSe_12)]]
+
−
 
+
−
==Aufgabe 2.4==
+
−
Wir gehen von folgender Implikation aus: Wenn zwei Geraden g und h nicht identisch sind, dann haben sie höchstens einen Punkt gemeinsam.<br />
+
−
a) Wie lautet die Kontraposition dieser Implikation?<br />
+
−
b) Wie lautet die Annahme, wenn Sie diese Implikation durch einen Widerspruch beweisen möchten?<br />
+
−
[[Lösung von Aufgabe 2.4_S (SoSe_12)]]
+
−
 
+
−
==Aufgabe 2.5==
+
−
Es seien A und B zwei Punktmengen. Was müssen Sie konkret zeigen, wenn Sie beweisen wollen, dass A = B ?<br />
+
−
 
+
−
[[Lösung von Aufgabe 2.5_S (SoSe_12)]]
+
−
 
+
−
==Aufgabe 2.6==
+
 
Das Parallelenaxiom lautet wie folgt:<br />  
 
Das Parallelenaxiom lautet wie folgt:<br />  
 
Zu jeder Geraden ''g'' und zu jedem nicht auf ''g'' liegenden Punkt ''A'' gibt es höchstens eine Gerade, die durch ''A'' verläuft und zu ''g'' parallel ist.<br />  
 
Zu jeder Geraden ''g'' und zu jedem nicht auf ''g'' liegenden Punkt ''A'' gibt es höchstens eine Gerade, die durch ''A'' verläuft und zu ''g'' parallel ist.<br />  
Zeile 54: Zeile 42:
 
a) Beweisen Sie folgende Implikation durch einen Widerspruchsbeweis: <math>\ a \|| b \wedge b \|| c \Rightarrow \ a \|| c</math>  . <br />
 
a) Beweisen Sie folgende Implikation durch einen Widerspruchsbeweis: <math>\ a \|| b \wedge b \|| c \Rightarrow \ a \|| c</math>  . <br />
 
b) Welche Eigenschaft der Relation <math>\|| </math> auf der Menge aller Geraden einer Ebene haben Sie hiermit gezeigt?<br />
 
b) Welche Eigenschaft der Relation <math>\|| </math> auf der Menge aller Geraden einer Ebene haben Sie hiermit gezeigt?<br />
−
[[Lösung von Aufgabe 2.6_S (SoSe_12)]]
+
[[Lösung von Aufgabe 3.4_S (SoSe_12)]]
 +
 
 +
 
 +
==Aufgabe 3.5==
 +
Gegeben sei folgende Äquivalenz: Der Abstand zweier Punkte ''A'' und ''B'' ist genau dann 0, wenn ''A'' und ''B'' identisch sind.<br />
 +
a) Formulieren Sie die beiden Implikationen, die in dieser Aussage stecken.<br />
 +
b) Wie lautet jeweils die Kontraposition der beiden Implikationen?<br />
 +
c) Wie lauten die beiden Annahmen, wenn Sie diese Implikationen jeweils durch einen Widerspruch beweisen möchten?<br />
 +
[[Lösung von Aufgabe 3.5_S (SoSe_12)]]
  
  
 
[[Category:Einführung_S]]
 
[[Category:Einführung_S]]

Aktuelle Version vom 26. April 2012, 14:36 Uhr

Inhaltsverzeichnis

Aufgaben zu Definitionen

Aufgabe 3.1

Unter einer Konventionaldefinition versteht man eine Definition, die in der Form "Wenn-Dann" formuliert wurde.
Geben Sie zwei prinzipiell verschiedene Konventionaldefinitionen des Begriffs Mittelsenkrechte einer Strecke an.
Lösung von Aufgabe 3.1_S (SoSe_12)


Aufgaben zu Sätzen und Beweisen

Aufgabe 3.2

Wir gehen von folgender Implikation aus: Wenn zwei Geraden g und h nicht identisch sind, dann haben sie höchstens einen Punkt gemeinsam.
a) Wie lautet die Kontraposition dieser Implikation?
b) Wie lautet die Annahme, wenn Sie diese Implikation durch einen Widerspruch beweisen möchten?
Lösung von Aufgabe 3.2_S (SoSe_12)

Aufgabe 3.3

Satz: In einem Dreieck \overline{ABC} mit |AC|< |BC| < |AB| sind die Winkel α und β nicht kongruent zueinander.

a) Welcher Beweis ist korrekt? Begründen Sie ausführlich! (Der Basiswinkelsatz und seine Umkehrung seien bereits bewiesen.)

Beweis 1) Sei \overline{ABC} ein Dreieck.
Vor: |AC|< |BC| < |AB|.
Beh: |α| ≠ |β|
Bew: Da nach Voraussetzung |AC| ≠ |BC| gilt nach dem Basiswinkelsatz |α| ≠ |β|. Damit ist der Satz bewiesen.

Beweis 2) Sei \overline{ABC} ein Dreieck.
Vor: |AC|< |BC| < |AB|.
Beh: |α| ≠ |β|
Bew: Nach Umkehrung des Basiswinkelsatzes gilt: Wenn |α|= |β| dann gilt |AC|= |BC|. Die Kontraposition der Umkehrung lautet also: Wenn |AC| ≠ |BC| dann gilt |α| ≠ |β|. Da die Kontraposition gleichwertig ist, kann man auch diese beweisen. Da nach Voraussetzung gilt: |AC|< |BC|, d.h. |AC| ≠ |BC|, kann nach Kontraposition der Umkehrung des Basiswinkelsatzes direkt gefolgert werden: |α| ≠ |β|. Damit ist der Satz bewiesen.

b) Beweisen Sie den Satz indirekt mit Widerspruch.

Lösung von Aufgabe 3.3_S (SoSe_12)

Aufgabe 3.4

Das Parallelenaxiom lautet wie folgt:
Zu jeder Geraden g und zu jedem nicht auf g liegenden Punkt A gibt es höchstens eine Gerade, die durch A verläuft und zu g parallel ist.
Nutzen Sie dieses Axiom, beim Lösen der folgenden Aufgabe:
Es seien a, b und c drei paarweise verschiedene Geraden in ein und derselben Ebene.
a) Beweisen Sie folgende Implikation durch einen Widerspruchsbeweis: 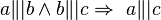\ a \|| b \wedge b \|| c \Rightarrow \ a \|| c .
b) Welche Eigenschaft der Relation \|| auf der Menge aller Geraden einer Ebene haben Sie hiermit gezeigt?
Lösung von Aufgabe 3.4_S (SoSe_12)


Aufgabe 3.5

Gegeben sei folgende Äquivalenz: Der Abstand zweier Punkte A und B ist genau dann 0, wenn A und B identisch sind.
a) Formulieren Sie die beiden Implikationen, die in dieser Aussage stecken.
b) Wie lautet jeweils die Kontraposition der beiden Implikationen?
c) Wie lauten die beiden Annahmen, wenn Sie diese Implikationen jeweils durch einen Widerspruch beweisen möchten?
Lösung von Aufgabe 3.5_S (SoSe_12)

Von „http://geometrie.zum.de/index.php?title=Übung_Aufgaben_2_(SoSe_12)&oldid=12304“