Lösung von Aufg. 10.2 S: Unterschied zwischen den Versionen
(→Kopernikus / Just noch ein sailA) |
(→Kopernikus / Just noch ein sailA) |
||
| (11 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 7: | Zeile 7: | ||
(V1) Punkt P<br /> | (V1) Punkt P<br /> | ||
(V2) Strecke <math>\overline{AB}</math><br /> | (V2) Strecke <math>\overline{AB}</math><br /> | ||
| − | (V3) <math>\left| | + | (V3) <math>\left|PA| = |PB| = \left| d \right|</math> bzw. <math>\overline {PA} \tilde {=} \overline {PB}</math><br /> |
'''Behauptung:'''<br /> | '''Behauptung:'''<br /> | ||
P <math>\in</math> Mittelsenkrechte<math>\overline{AB}</math> <br /> | P <math>\in</math> Mittelsenkrechte<math>\overline{AB}</math> <br /> | ||
(1) <math>\exist M\in \overline{AB} : \left| AM \right| = \left| MB \right|</math> // (V2), Ex. & Eind. Mittelpkt. einer Strecke<br /> | (1) <math>\exist M\in \overline{AB} : \left| AM \right| = \left| MB \right|</math> // (V2), Ex. & Eind. Mittelpkt. einer Strecke<br /> | ||
| − | (2) <math>\exists m \in E : \ | + | (2) <math>\exists m \in E : \ M,P \in m</math> // (V1), (1), Axiom I.1<br /> |
| − | (3) <math>\overline{MP} = \overline{MP}</math> // trivial<br /> | + | (3) <math>\overline{MP} \tilde {=} \overline{MP}</math> // trivial<br /> |
| − | (4) <math> | + | (4) <math>\overline {PA} \tilde {=} \overline {PB}</math> // (V3) <br /> |
| − | (5) <math> | + | (5) <math>\overline {AM} \tilde {=} \overline {MB}</math> // (1) <br /> |
| − | (6) <math>\overline{AMP} | + | (6) <math>\overline{AMP} \tilde {=} \overline{BMP}</math> // (3-5), SSS <br /> |
| − | (7) <math>\angle AMP | + | (7) <math>\angle AMP \tilde {=} \angle BMP </math> // (6) <br /> |
(8) <math>\ m \perp \overline{AB}</math> // (7), Def. NW, Def. suppl., Supplementaxiom, Def. rechter Winkel, Def. senkrecht <br /> | (8) <math>\ m \perp \overline{AB}</math> // (7), Def. NW, Def. suppl., Supplementaxiom, Def. rechter Winkel, Def. senkrecht <br /> | ||
(9) <math>P \in m</math> also auch <math>P \in Mittelsenkrechte \overline{AB}</math> // (2)<br /> | (9) <math>P \in m</math> also auch <math>P \in Mittelsenkrechte \overline{AB}</math> // (2)<br /> | ||
| Zeile 31: | Zeile 31: | ||
<br /> | <br /> | ||
1. <math>\overline{AB}</math> <br /> | 1. <math>\overline{AB}</math> <br /> | ||
| − | 2. <math>\ | + | 2. <math>\left| AP \right| =\left| BP \right|</math> |
<br /><br /> | <br /><br /> | ||
''' Beh: '''<br /> | ''' Beh: '''<br /> | ||
| − | <math>P\in</math> | + | <math>P\in</math> Satz III.1: (Existenz und Eindeutigkeit des Mittelpunkte einer Strecke) von <math>\overline{AB}</math> |
<br /> | <br /> | ||
| Zeile 43: | Zeile 43: | ||
|- | |- | ||
| 1 | | 1 | ||
| − | | <math>\ | + | | <math>\left| AP \right| =\left| BP \right|</math> |
| Vor. | | Vor. | ||
|- | |- | ||
| 2 | | 2 | ||
| <math>\overline{AM} =\overline{MB}</math> | | <math>\overline{AM} =\overline{MB}</math> | ||
| − | | | + | | Satz III.1: (Existenz und Eindeutigkeit des Mittelpunkte der Strecke <math>\overline{AB}</math> |
|- | |- | ||
| 3 | | 3 | ||
| Zeile 71: | Zeile 71: | ||
|} | |} | ||
--[[Benutzer:Kopernikus|Kopernikus]] 15:50, 28. Jun. 2012 (CEST)<br /><br /> | --[[Benutzer:Kopernikus|Kopernikus]] 15:50, 28. Jun. 2012 (CEST)<br /><br /> | ||
| − | |||
| − | |||
== == | == == | ||
<math>\overline{AB}</math> | <math>\overline{AB}</math> | ||
| + | |||
| + | |||
| + | Lösungsversuch schokomuffin | ||
| + | |||
| + | Vor: <math>|PA| = |PB|</math><br /> | ||
| + | Beh: <math>P \in</math> Mittelsenkrechte von <math>\overline{AB}</math> <br /> | ||
| + | |||
| + | (1) <math>\exists M \in \overline{AB} : \left| AM \right| = \left| MB \right|</math> Ex. u. Eind. Mittelpunkt, Ax. II/ 2 | ||
| + | |||
| + | (2) <math>\exists g : M \in g \ \wedge P \in g</math> Ax. I/1 | ||
| + | |||
| + | (3) <math>\angle BMP = 90</math> Ax. IV/2 | ||
| + | |||
| + | (4) <math>\angle AMP = \angle BMP</math> Def. RW, NW, (3) | ||
| + | |||
| + | (5) <math>\ g \perp \ \overline{AB}</math> (4), (3) | ||
| + | |||
| + | (6) g ist Mittelsenkrechte von <math>\overline{AB}</math> (4), (1) | ||
| + | |||
| + | --[[schokomuffin]] 14:02 01. Jul. 2012 (CEST)<br /><br /> | ||
| + | *Schritt 3 und Schritt 4 kommen mir etwas aus der Luft gegriffen vor. Woher weiß man, dass <math>\angle BMP = 90</math> und <math>\angle AMP = \angle BMP</math> gilt? --[[Benutzer:Andreas|Tutor Andreas]] 20:12, 1. Jul. 2012 (CEST) | ||
| + | [[Kategorie:Einführung_S]] | ||
Aktuelle Version vom 3. Juli 2012, 12:32 Uhr
Lösungsversuch Nummero6/Tchu Tcha Tcha:
Skizze:
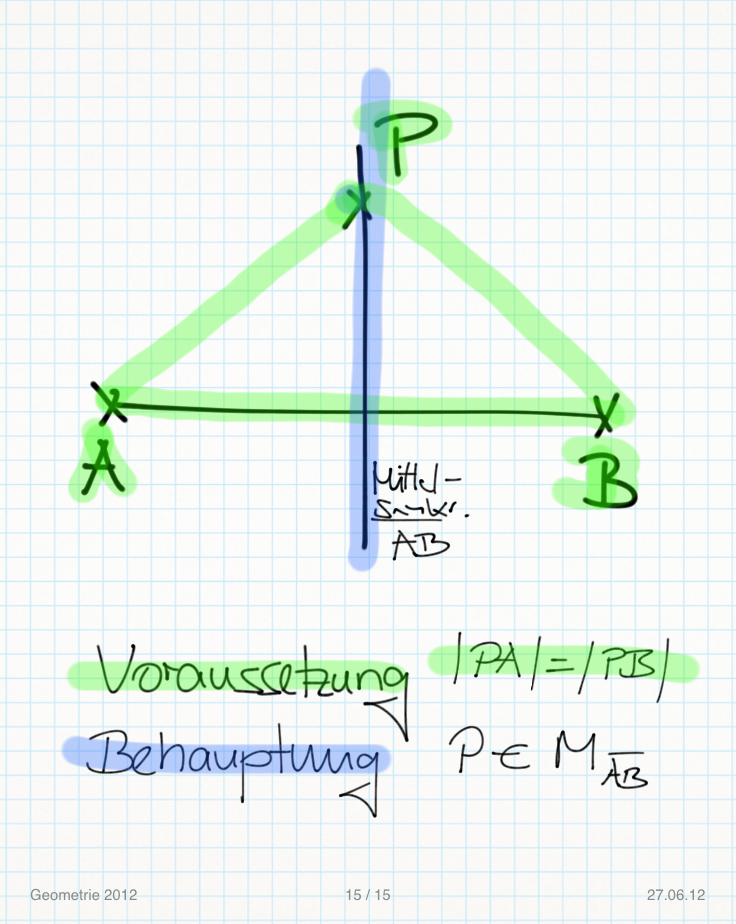
Voraussetzung:
(V1) Punkt P
(V2) Strecke 
(V3) Fehler beim Parsen(Syntaxfehler): \left|PA| = |PB| = \left| d \right|
bzw.
Behauptung:
P  Mittelsenkrechte
Mittelsenkrechte
(1) 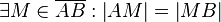 // (V2), Ex. & Eind. Mittelpkt. einer Strecke
// (V2), Ex. & Eind. Mittelpkt. einer Strecke
(2) 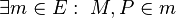 // (V1), (1), Axiom I.1
// (V1), (1), Axiom I.1
(3) 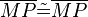 // trivial
// trivial
(4) 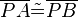 // (V3)
// (V3)
(5) 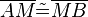 // (1)
// (1)
(6) 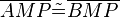 // (3-5), SSS
// (3-5), SSS
(7) 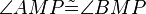 // (6)
// (6)
(8) 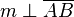 // (7), Def. NW, Def. suppl., Supplementaxiom, Def. rechter Winkel, Def. senkrecht
// (7), Def. NW, Def. suppl., Supplementaxiom, Def. rechter Winkel, Def. senkrecht
(9) 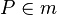 also auch
also auch 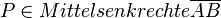 // (2)
// (2)
qed
--Tchu Tcha Tcha 18:58, 27. Jun. 2012 (CEST)
Kopernikus / Just noch ein sailA
Beweisen Sie Satz VII.6 a:
Wenn ein Punkt  zu den Endpunkten der Strecke
zu den Endpunkten der Strecke  jeweils ein und denselben Abstand hat, so ist er ein Punkt der Mittelsenkrechten von
jeweils ein und denselben Abstand hat, so ist er ein Punkt der Mittelsenkrechten von  .
.
Vor:
1. 
2. 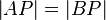
Beh:
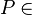 Satz III.1: (Existenz und Eindeutigkeit des Mittelpunkte einer Strecke) von
Satz III.1: (Existenz und Eindeutigkeit des Mittelpunkte einer Strecke) von 
| Schritt | Beweis | Begründung |
|---|---|---|
| 1 | 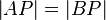
|
Vor. |
| 2 | 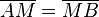
|
Satz III.1: (Existenz und Eindeutigkeit des Mittelpunkte der Strecke 
|
| 3 | 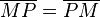
|
trivial |
| 4 | 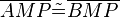
|
Kong. Satz SSS, 1,2,3 |
| 5 | 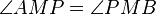
|
4, Dreieckskongruenz |
| 6 | 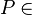 der Mittelsenkrechten von der Mittelsenkrechten von 
|
2,5, Def. VI.1 (Mittelsenkrechte) |
| 7 | Beh. stimmt q.e.d | 6, Beh. |
--Kopernikus 15:50, 28. Jun. 2012 (CEST)

Lösungsversuch schokomuffin
Vor: 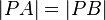
Beh: 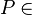 Mittelsenkrechte von
Mittelsenkrechte von 
(1) 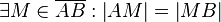 Ex. u. Eind. Mittelpunkt, Ax. II/ 2
Ex. u. Eind. Mittelpunkt, Ax. II/ 2
(2) 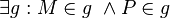 Ax. I/1
Ax. I/1
(3) 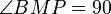 Ax. IV/2
Ax. IV/2
(4) 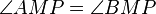 Def. RW, NW, (3)
Def. RW, NW, (3)
(5) 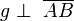 (4), (3)
(4), (3)
(6) g ist Mittelsenkrechte von  (4), (1)
(4), (1)
--schokomuffin 14:02 01. Jul. 2012 (CEST)
- Schritt 3 und Schritt 4 kommen mir etwas aus der Luft gegriffen vor. Woher weiß man, dass
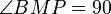 und
und 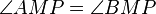 gilt? --Tutor Andreas 20:12, 1. Jul. 2012 (CEST)
gilt? --Tutor Andreas 20:12, 1. Jul. 2012 (CEST)

