Serie 5 (WS 12 13): Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „=Aufgaben zum Abstand= ==Aufgabe 5.1== <u>'''Satz:'''</u> ::Von drei paarweise verschiedenen Punkten <math>\ A, B</math> und <math>\ C</math> ein und derselben G…“) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 5.7: Helfen Sie Yellow) |
||
| (38 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | = | + | <div style="margin:0; margin-right:4px; border:1px solid #27408B; padding: 1em 1em 1em 1em; background-color:#FFFF99; align:left;"> |
| + | {|width=90%| style="background-color:#FFFF99; padding:1em" | ||
| + | | valign="top" | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| + | |||
| + | |||
| + | =weitere Aufgaben zur Inzidenz= | ||
| + | „Man muß jederzeit an Stelle von ‚Punkten‘, ‚Geraden‘, ‚Ebenen‘, ‚Tische‘, ‚Stühle‘, ‚Bierseidel‘ sagen | ||
| + | können.“<br /> | ||
| + | David Hilbert (1862-1943) | ||
| + | ==Aufgabe 5.1== | ||
| + | Begründen Sie: | ||
| + | #Jedes Modell für die Inzidenzaxiome der Ebene beinhaltet wenigstens 3 Punkte. | ||
| + | #Jedes Modell für die Inzidenzaxiome des Raumes beinhaltet wenigstens 4 Punkte. | ||
<br /> | <br /> | ||
[[Lösung von Aufgabe 5.1_S (WS_12_13)]] | [[Lösung von Aufgabe 5.1_S (WS_12_13)]] | ||
==Aufgabe 5.2== | ==Aufgabe 5.2== | ||
| − | + | Gegeben seien eine rote Kugel aus Knete (<math>R</math>), eine blaue Kugel aus Knete (<math>B</math>), eine grüne Kugel aus Knete (<math>G</math>) und eine schwarze Kugel aus Knete (<math>K</math>). Aus einem Mikadospiel wurde jeweils genau ein Repräsentant der folgenden Stäbchenart entnommen: Mikado, Mandarin, Bonzen und Samurai.<br /> | |
| − | <math> | + | Wir betrachten das folgende Modell für die Inzidenz:<br /> |
| + | *Menge aller Punkte <math>\mathbb{P}:=\{R. G, B, K\}</math> | ||
| + | *Menge aller Geraden <math>\mathbb{G}:=\{Mikado, Mandarin, Bonzen, Samurei, Kuli\}</math> | ||
| + | Die Inzidenzrelation interpretieren wir wie folgt: Ein Modellpunkt inziert mit einer Modellgeraden, wenn der Modellpunkt auf die Modellgerade gesteckt wurde.<br /> | ||
| + | Wir lassen die Modellpunkte mit den Modellgeraden jetzt wie folgt inzidieren: | ||
| + | * <math>R</math> und <math>G</math> inzidieren mit <math>Mikado</math> | ||
| + | * <math>G</math> und <math>B</math> inzidieren mit <math>Mandarin</math> | ||
| + | * <math>B</math> und <math>R</math> inzidieren mit <math>Bonzen</math> | ||
| + | * <math>R</math> und <math>K</math> inzidieren mit <math>Samurai</math> | ||
| + | * <math>G</math> und <math>K</math> inzidieren mit <math>Kuli</math> | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |||
| + | |- | ||
| + | |(a) || Fertigen Sie eine Skizze für dieses Modell an bzw. stellen Sie ein Foto von einem real gebauten Modell hier ein. | ||
| + | |- | ||
| + | |(b) || Nennen Sie drei verschiedene Gründe, warum dieses Modell kein Modell für die Inzidenzaxiome des Raumes ist. | ||
| + | |- | ||
| + | | (c) || Ergänzen Sie das Modell Sie derart, dass die Inzidenzaxiome I.1 bis I.7 erfüllt sind. | ||
| + | |- | ||
| + | | (d) || Mit dem von Ihnen ergänzten Modell haben Sie gezeigt, dass das Axiom I.0 unabhängig von den Axiomen I.1 bis I.7 ist. Warum? | ||
| + | |- | ||
| + | | (e) || Beweisen Sie: Wählt man zu unseren Knetekugeln als Modellgeraden Stäbchen eines originalen Mikadospiels derart, dass sich alle Geraden paarweise unterscheiden, so kann man kein Modell für die Inzidenzaxiome des Raumes bauen. | ||
| + | |||
| + | |} | ||
| − | |||
[[Lösung von Aufgabe 5.2_S (WS_12_13)]] | [[Lösung von Aufgabe 5.2_S (WS_12_13)]] | ||
==Aufgabe 5.3== | ==Aufgabe 5.3== | ||
| − | + | {{Definition|1=Zwei Geraden sind komplanar, wenn es eine Ebene gibt, die beide Geraden vollständig enthält.}} | |
| − | Wenn <math> | + | Beweisen Sie den folgenden Satz: <br /> |
| − | + | '''Satz *:'''<br /> | |
| + | ::Wenn zwei Geraden <math>g</math> und <math>h</math> genau einen Schnittpunkt haben, so sind sie komplanar. | ||
<br /> | <br /> | ||
[[Lösung von Aufgabe 5.3_S (WS_12_13)]] | [[Lösung von Aufgabe 5.3_S (WS_12_13)]] | ||
| − | |||
==Aufgabe 5.4== | ==Aufgabe 5.4== | ||
| − | + | Formulieren Sie Kontraposition und die Umkehrung von Satz * aus der Aufgabe 5.3. Äußern Sie sich zum Wahrheitgehalt dieser beiden Implikationen. Begründen Sie Ihre Äußerungen.<br /> | |
| − | <br /> | + | |
| − | |||
[[Lösung von Aufgabe 5.4_S (WS_12_13)]] | [[Lösung von Aufgabe 5.4_S (WS_12_13)]] | ||
| − | |||
| − | |||
| − | |||
== Aufgabe 5.5 == | == Aufgabe 5.5 == | ||
| − | + | Begründen Sie:<br /> | |
| + | Eine Definition des Begriffs der Komplanarität einer Punktmenge <math>M</math> macht nur Sinn, wenn <math>M</math> wenigstens vier Punkte enthält.<br /><br /> | ||
[[Lösung von Aufg. 5.5_S (WS_12_13)]]<br /> | [[Lösung von Aufg. 5.5_S (WS_12_13)]]<br /> | ||
<br /> | <br /> | ||
| + | |||
| + | == Aufgabe 5.6 == | ||
| + | Axiom I.7 liefert 4 Punkte, die nicht komplanar sind.<br /> | ||
| + | Es seien <math>A, B, C, D</math> diese 4 Punkte.<br /> | ||
| + | Sie dürfen im folgenden ohne Beweis davon ausgehen, dass je 4 nicht komplanare Punkte paarweise verschieden sind.<br /> | ||
| + | Es sei <math>\varepsilon</math> eine Ebene mit <math>A \in \varepsilon \wedge B \in \varepsilon</math>.<br /> | ||
| + | Beweisen Sie:<br /> | ||
| + | ::In <math>\varepsilon</math> existiert ein Punkt <math>P</math> mit <math>P \not= A \wedge P\not= B</math>.<br /><br /> | ||
| + | [[Lösung von Aufg. 5.6_S (WS_12_13)]]<br /> | ||
| + | <br /> | ||
| + | == Aufgabe 5.7: Helfen Sie Yellow== | ||
| + | In Aufgabe 4.3 war die Umkehrung der folgenden Implikation zu bilden: | ||
| + | Satz I: Wenn drei Punkte A, B, C nicht kollinear sind, so sind sie paarweise verschieden. | ||
| + | |||
| + | UserIn Yellow formulierte:<br /> | ||
| + | Wenn A,B,C paarweise verschieden sind, dann sind sie kollinar<br /> | ||
| + | Die Umkehrung entspricht dem Axiom I.3 und kann somit nicht bewiesen werden. | ||
| + | |||
| + | |||
| + | Was stimmt bei der Lösung von Yellow alles nicht? | ||
| + | |||
| + | [[Lösung von Aufg. 5.7_S (WS_12_13)]]<br /> | ||
| + | <br /> | ||
| + | <!--- Was hier drunter steht muss stehen bleiben ---> | ||
| + | |} | ||
| + | </div> | ||
| + | |||
| + | [[Kategorie:Einführung_S]] | ||
Aktuelle Version vom 24. November 2012, 15:27 Uhr
|
weitere Aufgaben zur Inzidenz„Man muß jederzeit an Stelle von ‚Punkten‘, ‚Geraden‘, ‚Ebenen‘, ‚Tische‘, ‚Stühle‘, ‚Bierseidel‘ sagen
können.“ Aufgabe 5.1Begründen Sie:
Aufgabe 5.2Gegeben seien eine rote Kugel aus Knete (
Die Inzidenzrelation interpretieren wir wie folgt: Ein Modellpunkt inziert mit einer Modellgeraden, wenn der Modellpunkt auf die Modellgerade gesteckt wurde.
Lösung von Aufgabe 5.2_S (WS_12_13) Aufgabe 5.3Definition Zwei Geraden sind komplanar, wenn es eine Ebene gibt, die beide Geraden vollständig enthält. Beweisen Sie den folgenden Satz:
Aufgabe 5.4Formulieren Sie Kontraposition und die Umkehrung von Satz * aus der Aufgabe 5.3. Äußern Sie sich zum Wahrheitgehalt dieser beiden Implikationen. Begründen Sie Ihre Äußerungen. Lösung von Aufgabe 5.4_S (WS_12_13) Aufgabe 5.5Begründen Sie: Aufgabe 5.6Axiom I.7 liefert 4 Punkte, die nicht komplanar sind.
Lösung von Aufg. 5.6_S (WS_12_13) Aufgabe 5.7: Helfen Sie YellowIn Aufgabe 4.3 war die Umkehrung der folgenden Implikation zu bilden: Satz I: Wenn drei Punkte A, B, C nicht kollinear sind, so sind sie paarweise verschieden. UserIn Yellow formulierte:
|
 ), eine blaue Kugel aus Knete (
), eine blaue Kugel aus Knete ( ), eine grüne Kugel aus Knete (
), eine grüne Kugel aus Knete ( ) und eine schwarze Kugel aus Knete (
) und eine schwarze Kugel aus Knete ( ). Aus einem Mikadospiel wurde jeweils genau ein Repräsentant der folgenden Stäbchenart entnommen: Mikado, Mandarin, Bonzen und Samurai.
). Aus einem Mikadospiel wurde jeweils genau ein Repräsentant der folgenden Stäbchenart entnommen: Mikado, Mandarin, Bonzen und Samurai.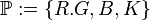
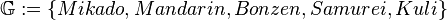
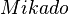
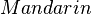
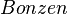
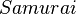
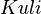
 und
und  genau einen Schnittpunkt haben, so sind sie komplanar.
genau einen Schnittpunkt haben, so sind sie komplanar.
 macht nur Sinn, wenn
macht nur Sinn, wenn 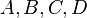 diese 4 Punkte.
diese 4 Punkte. eine Ebene mit
eine Ebene mit 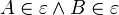 .
. mit
mit 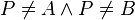 .
.
