|
weitere Aufgaben zur Inzidenz
„Man muß jederzeit an Stelle von ‚Punkten‘, ‚Geraden‘, ‚Ebenen‘, ‚Tische‘, ‚Stühle‘, ‚Bierseidel‘ sagen
können.“
David Hilbert (1862-1943)
Aufgabe 5.1
Begründen Sie:
- Jedes Modell für die Inzidenzaxiome der Ebene beinhaltet wenigstens 3 Punkte.
- Jedes Modell für die Inzidenzaxiome des Raumes beinhaltet wenigstens 4 Punkte.
Lösung von Aufgabe 5.1_S (WS_12_13)
Aufgabe 5.2
Gegeben seien eine rote Kugel aus Knete ( ), eine blaue Kugel aus Knete ( ), eine blaue Kugel aus Knete ( ), eine grüne Kugel aus Knete ( ), eine grüne Kugel aus Knete ( ) und eine schwarze Kugel aus Knete ( ) und eine schwarze Kugel aus Knete ( ). Aus einem Mikadospiel wurde jeweils genau ein Repräsentant der folgenden Stäbchenart entnommen: Mikado, Mandarin, Bonzen und Samurai. ). Aus einem Mikadospiel wurde jeweils genau ein Repräsentant der folgenden Stäbchenart entnommen: Mikado, Mandarin, Bonzen und Samurai.
Wir betrachten das folgende Modell für die Inzidenz:
- Menge aller Punkte
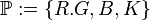
- Menge aller Geraden
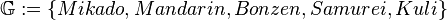
Die Inzidenzrelation interpretieren wir wie folgt: Ein Modellpunkt inziert mit einer Modellgeraden, wenn der Modellpunkt auf die Modellgerade gesteckt wurde.
Wir lassen die Modellpunkte mit den Modellgeraden jetzt wie folgt inzidieren:
-
 und und  inzidieren mit inzidieren mit 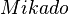
-
 und und  inzidieren mit inzidieren mit 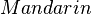
-
 und und  inzidieren mit inzidieren mit 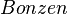
-
 und und  inzidieren mit inzidieren mit 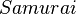
-
 und und  inzidieren mit inzidieren mit 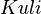
| (a) |
Fertigen Sie eine Skizze für dieses Modell an bzw. stellen Sie ein Foto von einem real gebauten Modell hier ein.
|
| (b) |
Nennen Sie drei verschiedene Gründe, warum dieses Modell kein Modell für die Inzidenzaxiome des Raumes ist.
|
| (c) |
Ergänzen Sie das Modell Sie derart, dass die Inzidenzaxiome I.1 bis I.7 erfüllt sind.
|
| (d) |
Mit dem von Ihnen ergänzten Modell haben Sie gezeigt, dass das Axiom I.0 unabhängig von den Axiomen I.1 bis I.7 ist. Warum?
|
| (e) |
Beweisen Sie: Wählt man zu unseren Knetekugeln als Modellgeraden Stäbchen eines originalen Mikadospiels derart, dass sich alle Geraden paarweise unterscheiden, so kann man kein Modell für die Inzidenzaxiome des Raumes bauen.
|
Lösung von Aufgabe 5.2_S (WS_12_13)
Aufgabe 5.3
Definition
Zwei Geraden sind komplanar, wenn es eine Ebene gibt, die beide Geraden vollständig enthält.
Beweisen Sie den folgenden Satz:
Satz *:
- Wenn zwei Geraden
 und und  genau einen Schnittpunkt haben, so sind sie komplanar. genau einen Schnittpunkt haben, so sind sie komplanar.
Lösung von Aufgabe 5.3_S (WS_12_13)
Aufgabe 5.4
Formulieren Sie Kontraposition und die Umkehrung von Satz * aus der Aufgabe 5.3. Äußern Sie sich zum Wahrheitgehalt dieser beiden Implikationen. Begründen Sie Ihre Äußerungen.
Lösung von Aufgabe 5.4_S (WS_12_13)
Aufgabe 5.5
Begründen Sie:
Eine Definition des Begriffs der Komplanarität einer Punktmenge  macht nur Sinn, wenn macht nur Sinn, wenn  wenigstens vier Punkte enthält. wenigstens vier Punkte enthält.
Lösung von Aufg. 5.5_S (WS_12_13)
Aufgabe 5.6
Axiom I.7 liefert 4 Punkte, die nicht komplanar sind.
Es seien 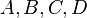 diese 4 Punkte. diese 4 Punkte.
Sie dürfen im folgenden ohne Beweis davon ausgehen, dass je 4 nicht komplanare Punkte paarweise verschieden sind.
Es sei  eine Ebene mit eine Ebene mit 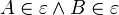 . .
Beweisen Sie:
- In
 existiert ein Punkt existiert ein Punkt  mit mit 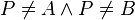 . .
Lösung von Aufg. 5.6_S (WS_12_13)
Aufgabe 5.7: Helfen Sie Yellow
In Aufgabe 4.3 war die Umkehrung der folgenden Implikation zu bilden:
Satz I: Wenn drei Punkte A, B, C nicht kollinear sind, so sind sie paarweise verschieden.
UserIn Yellow formulierte:
Wenn A,B,C paarweise verschieden sind, dann sind sie kollinar
Die Umkehrung entspricht dem Axiom I.3 und kann somit nicht bewiesen werden.
Was stimmt bei der Lösung von Yellow alles nicht?
Lösung von Aufg. 5.7_S (WS_12_13)
|  ), eine blaue Kugel aus Knete (
), eine blaue Kugel aus Knete ( ), eine grüne Kugel aus Knete (
), eine grüne Kugel aus Knete ( ) und eine schwarze Kugel aus Knete (
) und eine schwarze Kugel aus Knete ( ). Aus einem Mikadospiel wurde jeweils genau ein Repräsentant der folgenden Stäbchenart entnommen: Mikado, Mandarin, Bonzen und Samurai.
). Aus einem Mikadospiel wurde jeweils genau ein Repräsentant der folgenden Stäbchenart entnommen: Mikado, Mandarin, Bonzen und Samurai.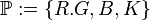
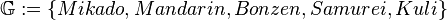
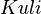
 und
und  genau einen Schnittpunkt haben, so sind sie komplanar.
genau einen Schnittpunkt haben, so sind sie komplanar.
 macht nur Sinn, wenn
macht nur Sinn, wenn 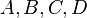 diese 4 Punkte.
diese 4 Punkte. eine Ebene mit
eine Ebene mit 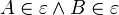 .
. mit
mit 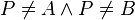 .
.
