Halbebenen oder das Axiom von Pasch: Unterschied zwischen den Versionen
(→Definition IV.1: (offene Halbebene)) |
(→Neuer Versuch (siehe Diskussionsseite)) |
||
| (92 dazwischenliegende Versionen von 7 Benutzern werden nicht angezeigt) | |||
| Zeile 18: | Zeile 18: | ||
|- | |- | ||
| <math>\ G</math> ist eine Gerade | | <math>\ G</math> ist eine Gerade | ||
| − | | <math>\ G</math> ist eine | + | | <math>\ G</math> ist eine Ebene |
|- | |- | ||
| Zeile 24: | Zeile 24: | ||
|- | |- | ||
| − | | | + | | eindimensional |
| − | | | + | | zweidimensional |
|- | |- | ||
| Zeile 31: | Zeile 31: | ||
|- | |- | ||
| − | | | + | | Anfangspunkt <math>\ A</math> |
| − | | | + | | Trägergerade <math>\ g</math> |
|- | |- | ||
| Zeile 38: | Zeile 38: | ||
|- | |- | ||
| − | | | + | | nulldimensional |
| − | | | + | | eindimensional |
|- | |- | ||
| Zeile 50: | Zeile 50: | ||
|- | |- | ||
| − | | <math>\ AQ^{+} = \{P| | + | | <math>\ AQ^{+} = \{P| A \not \in \overline{PQ} \} </math> an dieser Stelle sind noch zwei Präzisierungen notwendig:<br/> 1: es muss sichergestellt sein, dass <math> P </math> Element der Geraden <math> AQ </math> ist und <br/> 2: der Punkt <math> A </math> selbst muss noch berücksichtigt werden:<br/> |
| − | | <math>\ gQ^{+} = \{P| | + | <math>\ AQ^{+} = \{P \in AQ| A \not \in \overline{PQ}\} \cup \{A\} </math> |
| + | | <math>\ gQ^{+} = \{P| g\cap\overline {PQ} =\{\}\}</math> | ||
|- | |- | ||
| Zeile 59: | Zeile 60: | ||
|- | |- | ||
| − | | <math>\ AQ^{-} = \{P| | + | | <math>\ AQ^{-} = \{P| A \in \overline{PQ} \} </math> |
| − | | <math>\ gQ^{-} = \{P| | + | | <math>\ gQ^{-} = \{P| \neg \exist S : g\cap\overline {PQ} =\{S\} \}</math> |
|} | |} | ||
| + | --[[Benutzer:*m.g.*|*m.g.*]] 20:00, 23. Jun. 2010 (UTC) | ||
| − | + | Was ich nicht verstanden habe ist, warum die Dimension vom Anfangspunkt A gleich eins ist und die Dimension von der Trägergeraden gleich zwei? Soweit ich weiß, hat ein Punkt die Dimension null und eine Gerade die Dimension 1. | |
| − | + | Entschuldigung, mein Fehler: Ein Punkt hat natürlich die Dimension 0 und eine Gerade die Dimension 1. --[[Benutzer:*m.g.*|*m.g.*]] 17:00, 27. Jun. 2010 (UTC) | |
| − | + | ||
| − | + | Zu gQ+: | |
| − | + | Wenn hier von der geschlossenen Halbebene die Rede ist, fehlen alle Punkte die auf der Trägergeraden liegen und auch dazu gehören... | |
| − | + | ||
| − | + | Zu gQ-: | |
| + | Ausformuliert steht hier: gQ- ist die Menge aller Punkte, für die gilt, dass es KEINEN Schnittpunkt von g und der Strecke PQ (mit Dächle) gibt.. | ||
| + | Wenn ich es richtig verstanden habe ist das natürlich quatsch. Voraussetzung ist, dass sie einen Schnittpunkt haben, sonst lägen sie ja in derselben HE wie Q! | ||
| + | |||
| + | --[[Benutzer:Principella|Principella]] 21:42, 20. Jul. 2010 (UTC) | ||
=== Definition des Begriffs der Halbebene === | === Definition des Begriffs der Halbebene === | ||
| Zeile 86: | Zeile 92: | ||
Die beiden Seiten, in die die Menge der Punkte einer Ebene <math>\ \Epsilon</math>, die nicht auf einer Geraden <math>\ g</math> dieser Ebene liegen, durch diese Gerade <math>\ g</math> eingeteilt wird, heißen offene Halbebenen von <math>\ \Epsilon</math> bezüglich der Trägergeraden <math>\ g</math>. Der nicht zu <math>\ g</math> gehörende Referenzpunkt <math>\ Q \in \Epsilon</math> bietet uns eine Möglichkeit zur Bezeichnung der beiden offenen Halbebenen. Die offene Halbebene, zu der alle Punkte gehören, die bezüglich <math>\ g</math> mit <math>\ Q</math> auf derselben Seite liegen, wird mit <math>\ gQ^{+}</math> bezeichnet, die andere offene Halbebene von <math>\ \Epsilon</math> bezüglich <math>\ g</math> und <math>\ Q</math> mit <math>\ gQ^{-}</math>. | Die beiden Seiten, in die die Menge der Punkte einer Ebene <math>\ \Epsilon</math>, die nicht auf einer Geraden <math>\ g</math> dieser Ebene liegen, durch diese Gerade <math>\ g</math> eingeteilt wird, heißen offene Halbebenen von <math>\ \Epsilon</math> bezüglich der Trägergeraden <math>\ g</math>. Der nicht zu <math>\ g</math> gehörende Referenzpunkt <math>\ Q \in \Epsilon</math> bietet uns eine Möglichkeit zur Bezeichnung der beiden offenen Halbebenen. Die offene Halbebene, zu der alle Punkte gehören, die bezüglich <math>\ g</math> mit <math>\ Q</math> auf derselben Seite liegen, wird mit <math>\ gQ^{+}</math> bezeichnet, die andere offene Halbebene von <math>\ \Epsilon</math> bezüglich <math>\ g</math> und <math>\ Q</math> mit <math>\ gQ^{-}</math>. | ||
| − | Obige Ausführungen können als informelle Definition des Begriffs offene Halbebene dienen. Hinsichtlich wirklicher mathematischer Exaktheit der Festlegung, was denn eine offene Halbene sein möge, bedarf es einer genauereren Erklärung, was | + | Obige Ausführungen können als informelle Definition des Begriffs offene Halbebene dienen. Hinsichtlich wirklicher mathematischer Exaktheit der Festlegung, was denn eine offene Halbene sein möge, bedarf es einer genauereren Erklärung, was denn darunter zu verstehen wäre, dass zwei Punkte <math>\ P</math> und <math> \ Q</math> einer Ebene <math>\ \Epsilon</math> auf ein und derselben bzw. auf zwei verschiedenen Seiten dieser Ebene bezüglich einer Geraden <math>\ g</math> liegen. |
===== Definition IV.1: (offene Halbebene)===== | ===== Definition IV.1: (offene Halbebene)===== | ||
| − | :::Es sei <math>\ \Epsilon</math> eine Ebene in der die Gerade <math>\ g</math> liegen möge. Ferner sei <math>\ Q</math> ein Punkt der Ebene <math>\ \Epsilon</math>, der nicht zur Geraden <math>\ g</math> gehört.<br /> Unter den offenen Halbebenen <math>\ gQ^{+}</math> und <math>\ gQ^{-}</math> bezüglich der Trägergeraden <math>\ g</math> versteht man die folgenden | + | :::Es sei <math>\ \Epsilon</math> eine Ebene in der die Gerade <math>\ g</math> liegen möge. Ferner sei <math>\ Q</math> ein Punkt der Ebene <math>\ \Epsilon</math>, der nicht zur Geraden <math>\ g</math> gehört.<br /> Unter den offenen Halbebenen <math>\ gQ^{+}</math> und <math>\ gQ^{-}</math> bezüglich der Trägergeraden <math>\ g</math> versteht man die folgenden Teilmengen der Ebene <math>\ \Epsilon</math> ohne die Gerade <math>\ g</math> : |
| − | ::::<math>\ gQ^{+}:= \{P| \neg\exists | + | ::::<math>\ gQ^{+}:= \{P| \neg\exists S \,\{S\}=g\cap\overline {PQ} \}</math> |
| − | |||
| − | + | ::::<math>\ gQ^{-}:= \{P| \exists S \,\{S\}=g\cap\overline {PQ} \} \setminus \{ g\}</math> | |
==== Halbebenen ==== | ==== Halbebenen ==== | ||
| Zeile 101: | Zeile 106: | ||
===== Definition IV.2: (Halbebene) ===== | ===== Definition IV.2: (Halbebene) ===== | ||
| − | ::: ... | + | ::Es sei <math>\ g</math> eine Gerade der Ebene <math>\ \Epsilon</math>. <math>\ gQ^+</math> und <math>\ gQ^-</math> seien die beiden offenen Halbebenen von <math>\ \Epsilon</math> bezüglich <math>\ g</math>. Unter den (geschlossenen) Halbebenen von <math>\ \Epsilon</math> bezüglich <math>\ g</math> versteht die beiden Punktmengen, die durch die Vereinigung jeder dieser beiden offenen Halbebene von <math>\ \Epsilon</math> bezüglich der Geraden <math>\ g</math> mit jeweils dieser Geraden <math>\ g</math> entstehen. |
| + | |||
| + | ::::<math>\ gQ^{+}:= \{P| \neg\exists S\,\{S\}=g\cap\overline {PQ} \} \cup \{g\}</math> | ||
| + | |||
| + | ::::<math>\ gQ^{-}:= \{P| \exists S\,\{S\}=g\cap\overline {PQ} \}</math> | ||
| + | |||
| + | |||
| + | Bemerkung: Für die formale Beschreibung von offenen und geschlossenen Halbebenen wird jeweils dieselbe Bezsichnung verwendet: offene Halbebene: <math>\ g Q^+</math>, (geschlossene) Halbebene: <math>\ g Q^+</math>. Derr weitere Gebrauch der Sprache kennzeichnet, ob es sich um eine offene oder um die geschlossene Halbene handeln soll. Aus Gründen der Vereinfachung sei vereinbart, dass <math>\ g Q^+</math> bzw. <math>\ g Q^-</math> immer die geschlossene Halbebene meint. Soll die offene Halbebene gemeint sein, so ist dieses durch den Zusatz "offen" zu kennzeichnen. | ||
| + | --[[Benutzer:*m.g.*|*m.g.*]] 21:50, 23. Jun. 2010 (UTC) | ||
== Die Repräsentantenunabhängigkeit des Referenzpunktes zweier Halbebenen == | == Die Repräsentantenunabhängigkeit des Referenzpunktes zweier Halbebenen == | ||
| Zeile 109: | Zeile 122: | ||
===== Beweis des Satzes IV.1 ===== | ===== Beweis des Satzes IV.1 ===== | ||
| − | + | ===== Neuer Versuch (siehe Diskussionsseite) ===== | |
| + | '''Voraussetzung:''' <math>Q_2 \in {gQ_1}^{+} </math> | ||
| + | <br />'''Behauptung:''' <math>{gQ_1}^{+} \equiv {gQ_2}^{+}</math> und <math>{gQ_1}^{-} \equiv {gQ_2}^{-}</math> | ||
| + | <br />'''Fallunterscheidung:''' | ||
| + | <br />Fall I <math>\ Q_1, Q_2</math> und <math>\ P</math> sind '''nicht kollinear'''. | ||
| + | <br />Fall II <math>\ Q_1, Q_2</math> und <math>\ P</math> '''sind kollinear'''. | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | ||'''Fall I''' <math>\ Q_1, Q_2</math> und <math>\ P</math> sind '''nicht kollinear'''. | ||
| + | |- | ||
| + | | ''Schritt''|| ''Aussage'' || ''Begründung'' | ||
| + | |- | ||
| + | | (1) || <math>{gQ_1}^{+} = \{P| \neg\exists S\,\{S\}=g\cap\overline {PQ_1} \} \cup \{g\}</math><br />Die Strecke <math>\overline {PQ_1}</math> schneidet '''nicht''' die Trägergerade g.|| Definition von Halbebene | ||
| + | |- | ||
| + | | (2) || <math>Q_2 \in {gQ_1}^{+}</math><br /> <math>Q_2</math> liegt in der Halbebene <math>{gQ_1}^{+}</math>|| Voraussetzung | ||
| + | |- | ||
| + | | (3) || <math>P,Q_1,Q_2 \in {gQ_1}^{+}</math>|| Schritt (1) und (2) | ||
| + | |- | ||
| + | | (4) || Da <math>\overline {PQ_1}</math> (Def. der Halbebene <math>{gQ_1}^{+}</math>) und <math>\overline {Q_1Q_2}</math> (nach Voraussetzung) keinen Schnittpunkt mit <math>g</math> haben, kann auch <math>\overline {PQ_2}</math> als dritte Seite des Dreiecks <math>\overline {PQ_1Q_2}</math>keinen Schnittpunkt mit g haben (da sonst Widerspruch mit Axiom von Pasch). | ||
| + | <br /> Die Strecke <math>\overline {PQ_2}</math> schneidet '''nicht''' die Trägergerade g. | ||
| + | || Schritt (3) und Satz von Pasch | ||
| + | |- | ||
| + | | (5) || <math>{gQ_2}^{+} = \{P| \neg\exists S\,\{S\}=g\cap\overline {PQ_2} \} \cup \{g\}</math>|| Schritt (4) | ||
| + | |- | ||
| + | | (6) || Es gilt: <math>{gQ_2}^{+} = \{P| \neg\exists S\,\{S\}=g\cap\overline {PQ_2} \} \cup \{g\}</math> und | ||
| + | <br /> <math>{gQ_1}^{+} = \{P| \neg\exists S\,\{S\}=g\cap\overline {PQ_2} \} \cup \{g\}</math>|| Voraussetzung und Schritt (5) | ||
| + | |- | ||
| + | | (7) || <math>{gQ_1}^{+} \equiv {gQ_2}^{+}</math>|| Der Definitionsbereich der beiden Halbebene ist identisch - Schritt (6) | ||
| + | |- | ||
| + | | (8) || <math>{gQ_1}^{-} \equiv {gQ_2}^{-}</math>|| Die Mengen <math>{gQ_1}^{+}</math> und <math>{gQ_1}^{-}</math>sind disjunkt, gleiches gilt für die Mengen <math>{gQ_2}^{+}</math> und <math>{gQ_2}^{-} | ||
| + | </math>Schritt (7) - Durch Umformung: | ||
| + | <br /> Ebene<math>\Epsilon = {gQ_1}^{+} \cup {gQ_1}^{-} \cup g</math> | ||
| + | <br /> Ebene<math>\Epsilon = {gQ_2}^{+} \cup {gQ_1}^{-} \cup g</math> | ||
| + | <br /> Da Ebene<math>\Epsilon = {gQ_2}^{+} \cup {gQ_2}^{-} \cup g</math> gilt somit auch <math>{gQ_1}^{-} \equiv {gQ_2}^{-}</math> | ||
| + | |} | ||
| + | |||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | ||'''Fall II''' <math>\ Q_1, Q_2</math> und <math>\ P</math> '''sind kollinear''', liegen auf der Geraden <math>\ h</math>. | ||
| + | |- | ||
| + | | ''Schritt''|| ''Aussage'' || ''Begründung'' | ||
| + | |- | ||
| + | | (1) || <math>{gQ_1}^{+} = \{P| \neg\exists S\,\{S\}=g\cap\overline {PQ_1} \} \cup \{g\}</math><br />Die Strecke <math>\overline {PQ_1}</math> schneidet '''nicht''' die Trägergerade g.|| Definition von Halbebene | ||
| + | |- | ||
| + | | (2) || <math>Q_2 \in {gQ_1}^{+}</math><br /> <math>Q_2</math> liegt in der Halbebene <math>{gQ_1}^{+}</math>, dadurch gilt: die Strecke <math>\overline {Q_1Q_2}</math> schneidet '''nicht''' die Trägergerade g.|| Voraussetzung und Definition von Halbebene | ||
| + | |- | ||
| + | | (3) || Wenn <math> \operatorname{koll} \left( Q_1, Q_2, P \right) </math> und <math>\ Q_1, Q_2, P</math> paarweise verschieden sind, dann gilt | ||
| + | <br /><math> \operatorname{Zw} \left( Q_1, Q_2, P \right) </math> oder | ||
| + | <br /><math> \operatorname{Zw} \left( Q_1, P, Q_2 \right) </math> oder | ||
| + | <br /><math> \operatorname{Zw} \left( Q_2, Q_1, P \right) </math>.|| Aus Voraussetzung '''kollinear''' und [http://wikis.zum.de/geowiki/index.php/Strecken#Satz_II.3 Satz II.3] | ||
| + | |- | ||
| + | | (4) || Wenn <math> \operatorname{Zw} \left( Q_1, Q_2, P \right) </math>, dann ist <math>\overline {PQ_2} \subset \overline {PQ_1}</math> und dadurch gilt <math>\overline {PQ_2} \in {gQ_1}^{+}</math> | ||
| + | || Zwischenrelation, Voraussetzung | ||
| + | |- | ||
| + | | (5) || Wenn <math> \operatorname{Zw} \left( Q_1, P, Q_2 \right) </math>, dann ist <math>\overline {PQ_2} \subset \overline {Q_1Q_2}</math> und dadurch gilt <math>\overline {PQ_2} \in {gQ_1}^{+}</math> | ||
| + | || Zwischenrelation, Voraussetzung | ||
| + | |- | ||
| + | | (6) || Wenn <math> \operatorname{Zw} \left( Q_2, Q_1, P \right)</math>, dann gehören alle Punkte der Strecke <math>\overline {PQ_2}</math> entweder zur Strecke <math>\overline {Q_1Q_2}</math> oder zur Strecke <math>\overline {PQ_1}</math>, für die gilt <math>\overline {Q_1Q_2} \in {gQ_1}^{+}</math> oder <math>\overline {PQ_1} \in {gQ_1}^{+}</math> | ||
| + | <br /> Dadurch gilt <math>\overline {PQ_2} \in {gQ_1}^{+}</math> | ||
| + | || Zwischenrelation, Aussagenlogik | ||
| + | |- | ||
| + | | (7) || Trivial, bzw. analog zu '''Fall I'''|| | ||
| + | |} | ||
| + | |||
| + | Stimmt das so? Nochmal geändert... | ||
| + | --[[Benutzer:Heinzvaneugen|Heinzvaneugen]] 15:10, 23. Jun. 2010 (UTC) | ||
| + | |||
| + | [[Bild:Dozenten.jpg]] | ||
| + | |||
| + | Analog dazu: [[Lösung_von_Aufgabe_8.1|Übungsaufgabe 8.1]]. Dort wird allerdings etwas anders vorgegangen, nämlich dass <math>R \notin {gQ}^{+} </math>. Die Analogie der Lösungen ergibt sich daraus, dass die Mengen disjunkt sind. | ||
| + | |||
| + | Müssen wir unbedingt unterscheiden, ob einmal kollinear und einmal nichtkollinear!? --[[Benutzer:TimoRR|TimoRR]] 08:51, 8. Jul. 2010 (UTC) | ||
| + | Oder geht das auch einfachso wie im folgenden eingescannten Beweise!? | ||
| + | [[Bild:Beweis Satz IV.1]] | ||
| + | --[[Benutzer:TimoRR|TimoRR]] 08:51, 8. Jul. 2010 (UTC) | ||
| + | |||
| + | Ich hab ein Problem mit der Voraussetzung: Wenn ich nur sage <math>Q_2 \in {gQ_1}^{+} </math>, dann kann <math>\ Q_2</math> doch immer noch ein Punkt auf g sein, oder sprechen wir von offenen Halbebenen? | ||
| + | Wenn nicht könnte also <math>\ Q_2</math> auf g liegen. Der "Referenzpunkt" einer Halbebene darf aber nicht auf der Trägergeraden liegen und so könnte <math>\ Q_2</math> kein "Referenzpunkt" sein... | ||
| + | Hat vielleicht jemand eine Ahnung??? | ||
| + | --[[Benutzer:Principella|Principella]] 22:31, 20. Jul. 2010 (UTC) | ||
| + | <br /><br />Ja, mir ist auch aufgefallen, dass es da ein bisschen durcheinander geht. <br />Ich würde mal behaupten, dass es bei dem oberen Beweisschema (Fall 1) unter '''Schritt 2''' (Voraussetzung, siehe Argument von Principella), '''Schritt 4''' (denn P kann ja auch auf g liegen, dann hat die geschlossene Strecke mit g eben doch einen Schnittpunkt) und in der Begründung von '''Schritt 8''' (auf einmal ist von disjunkten <u>offenen</u> Halbebenen die Rede, dabei wurde in Schritt 1 die Halbebene als geschlossen definiert) zu Problemen kommt. <br />Mein Vorschlag: Ich würde im gesamten Beweis mit offenen Halbebenen arbeiten. g gehört ja entweder zu beiden oder zu keiner der Halbebenen, hat also für deren Unterscheidung keine Relevanz.<br />--[[Benutzer:Barbarossa|Barbarossa]] 07:16, 21. Jul. 2010 (UTC) | ||
| + | |||
| + | Ich find du hast Recht, der Beweis sollte nur mit offenen Halbebenen geführt werden, denn nur so hat das mit de Repräsentanten überhaupt einen Sinn = Repräsentanten sind nur Repräsentanten einer offenen Halbebene, denn wenn sie Repräsentant beider Halbebenen sein könnten (im Fall der geschlossenen Halbebenen) wäre das Ganze ja sowieso quatsch... | ||
| + | --[[Benutzer:Principella|Principella]] 11:08, 21. Jul. 2010 (UTC) | ||
| + | |||
| + | Außerdem sprechen wir bei Referenzpunkten einer Halbebene von Repräsentanten einer Äquivalenzklasse und wie wir gelernt haben, müssen die drei Kriterien einer Klasseneiteilung erfüllt sein, d.h. die Teilmengen müssen auch disjunkt sein, was bei geschlossenen Halbebenen nicht gegeben ist. | ||
| + | |||
| + | Ich zitiere: "Ein Beispiel für eine Klasseneinteilung | ||
| + | |||
| + | Die übliche morgendliche Hektik an der „Maier-Vorwiesener“ Grund- und Hauptschule: Frau Schulze-Mackenroth zog es für heute vor, ihr Burnout-Syndrom mit Tannenzäpfle und Ouzo zu pflegen, weshalb sie sich kurz vor knapp bei Rektor Pollenwein telefonisch krank gemeldet hat. In ihrer Grundschulklasse geht es derweilen drunter und drüber. Xulio-Dävid hat seine überforderte, allein erziehende Mutter ausgetrickst und das Methylphenidat nicht genommen. Jetzt lässt er seine ADHS hemmungslos an seinen Klassenkameraden aus. | ||
| + | |||
| + | Zu Hause bei Lehrer Steiner gab es ein weiteres mal Stress wegen der jungen blonden Referendarin, die Steiner betreut. Er flüchtet deshalb und kommt eine Stunde früher. Erleichtert sieht ihn Rektor Gendarm beim Anmarsch auf die Schule. Aus dem Rektoratsfenster ruft er Steiner zu: „Du musst ganz schnell in die Klasse von Xulio-Dävid. Es brennt mal wieder!“ | ||
| + | |||
| + | Damit ist eindeutig geklärt, in welche Klasse Herr Steiner gehen muss. Rein formal hätte Rektor Gendarm natürlich auch die Namen von anderen Schülern nennen können, die mit Xulio-Dävid in dieselbe Klasse gehen. An der klassischen Grund- und Hauptschule geht jeder Schüler in genau eine Klasse. Ihre Klassen sind ein Beispiel dafür, was der Mathematiker unter einer Klasseneinteilung versteht." | ||
| + | |||
| + | Das Ganze ist analog zur Unabhängigkeit des Referenzpunktes zweier OFFENER HALBEBENEN zu sehen... | ||
| + | --[[Benutzer:Principella|Principella]] 20:32, 24. Jul. 2010 (UTC) | ||
== Das Axiom von [http://de.wikipedia.org/wiki/Moritz_Pasch Pasch] == | == Das Axiom von [http://de.wikipedia.org/wiki/Moritz_Pasch Pasch] == | ||
| Zeile 134: | Zeile 245: | ||
zu zeigen: Der Durchschnitt der beiden Mengen <math>\ M_1</math> und <math>\ M_2</math> ist auch konvex. | zu zeigen: Der Durchschnitt der beiden Mengen <math>\ M_1</math> und <math>\ M_2</math> ist auch konvex. | ||
| − | . | + | [[Lösung von Aufgabe 7.5]] |
Aktuelle Version vom 24. Juli 2010, 21:32 Uhr
Inhaltsverzeichnis |
Halbebenen und das Axiom von Pasch
Halbebenen
Analogiebetrachtungen
| |
|
 , das in Klassen eingeteilt wird , das in Klassen eingeteilt wird | |
 ist eine Gerade ist eine Gerade
|
 ist eine Ebene ist eine Ebene
|
 | |
| eindimensional | zweidimensional |
 , das , das  in Klassen einteilt in Klassen einteilt | |
Anfangspunkt 
|
Trägergerade 
|
 | |
| nulldimensional | eindimensional |
 teilt teilt 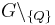 in genau zwei Klassen in genau zwei Klassen | |
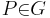 , die mit , die mit  bezüglich bezüglich  „auf derselben Seite liegen“ „auf derselben Seite liegen“ | |
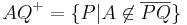 an dieser Stelle sind noch zwei Präzisierungen notwendig: an dieser Stelle sind noch zwei Präzisierungen notwendig:1: es muss sichergestellt sein, dass  Element der Geraden Element der Geraden 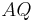 ist und ist und 2: der Punkt  selbst muss noch berücksichtigt werden: selbst muss noch berücksichtigt werden:
|
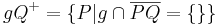
|
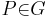 , die bezüglich , die bezüglich  nicht auf der Seite von nicht auf der Seite von  liegen. liegen. | |
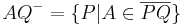
|
|
--*m.g.* 20:00, 23. Jun. 2010 (UTC)
Was ich nicht verstanden habe ist, warum die Dimension vom Anfangspunkt A gleich eins ist und die Dimension von der Trägergeraden gleich zwei? Soweit ich weiß, hat ein Punkt die Dimension null und eine Gerade die Dimension 1.
Entschuldigung, mein Fehler: Ein Punkt hat natürlich die Dimension 0 und eine Gerade die Dimension 1. --*m.g.* 17:00, 27. Jun. 2010 (UTC)
Zu gQ+: Wenn hier von der geschlossenen Halbebene die Rede ist, fehlen alle Punkte die auf der Trägergeraden liegen und auch dazu gehören...
Zu gQ-: Ausformuliert steht hier: gQ- ist die Menge aller Punkte, für die gilt, dass es KEINEN Schnittpunkt von g und der Strecke PQ (mit Dächle) gibt.. Wenn ich es richtig verstanden habe ist das natürlich quatsch. Voraussetzung ist, dass sie einen Schnittpunkt haben, sonst lägen sie ja in derselben HE wie Q!
--Principella 21:42, 20. Jul. 2010 (UTC)
Definition des Begriffs der Halbebene
Alles hat zwei Seiten oder grundlegende Ideen der Beschaffenheit von Ebenen
Offene Halbebenen
Die beiden Seiten, in die die Menge der Punkte einer Ebene  , die nicht auf einer Geraden
, die nicht auf einer Geraden  dieser Ebene liegen, durch diese Gerade
dieser Ebene liegen, durch diese Gerade  eingeteilt wird, heißen offene Halbebenen von
eingeteilt wird, heißen offene Halbebenen von  bezüglich der Trägergeraden
bezüglich der Trägergeraden  . Der nicht zu
. Der nicht zu  gehörende Referenzpunkt
gehörende Referenzpunkt 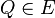 bietet uns eine Möglichkeit zur Bezeichnung der beiden offenen Halbebenen. Die offene Halbebene, zu der alle Punkte gehören, die bezüglich
bietet uns eine Möglichkeit zur Bezeichnung der beiden offenen Halbebenen. Die offene Halbebene, zu der alle Punkte gehören, die bezüglich  mit
mit  auf derselben Seite liegen, wird mit
auf derselben Seite liegen, wird mit  bezeichnet, die andere offene Halbebene von
bezeichnet, die andere offene Halbebene von  bezüglich
bezüglich  und
und  mit
mit  .
.
Obige Ausführungen können als informelle Definition des Begriffs offene Halbebene dienen. Hinsichtlich wirklicher mathematischer Exaktheit der Festlegung, was denn eine offene Halbene sein möge, bedarf es einer genauereren Erklärung, was denn darunter zu verstehen wäre, dass zwei Punkte  und
und  einer Ebene
einer Ebene  auf ein und derselben bzw. auf zwei verschiedenen Seiten dieser Ebene bezüglich einer Geraden
auf ein und derselben bzw. auf zwei verschiedenen Seiten dieser Ebene bezüglich einer Geraden  liegen.
liegen.
Definition IV.1: (offene Halbebene)
- Es sei
 eine Ebene in der die Gerade
eine Ebene in der die Gerade  liegen möge. Ferner sei
liegen möge. Ferner sei  ein Punkt der Ebene
ein Punkt der Ebene  , der nicht zur Geraden
, der nicht zur Geraden  gehört.
gehört.
Unter den offenen Halbebenen und
und  bezüglich der Trägergeraden
bezüglich der Trägergeraden  versteht man die folgenden Teilmengen der Ebene
versteht man die folgenden Teilmengen der Ebene  ohne die Gerade
ohne die Gerade  :
:
- Es sei
Halbebenen
Vereinigt man die Menge der Punkte einer offenen Halbeben mit der Menge der Punkte der Trägergerade so erhält man eine Halbebene.
Definition IV.2: (Halbebene)
- Es sei
 eine Gerade der Ebene
eine Gerade der Ebene  .
.  und
und 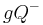 seien die beiden offenen Halbebenen von
seien die beiden offenen Halbebenen von  bezüglich
bezüglich  . Unter den (geschlossenen) Halbebenen von
. Unter den (geschlossenen) Halbebenen von  bezüglich
bezüglich  versteht die beiden Punktmengen, die durch die Vereinigung jeder dieser beiden offenen Halbebene von
versteht die beiden Punktmengen, die durch die Vereinigung jeder dieser beiden offenen Halbebene von  bezüglich der Geraden
bezüglich der Geraden  mit jeweils dieser Geraden
mit jeweils dieser Geraden  entstehen.
entstehen.
- Es sei
Bemerkung: Für die formale Beschreibung von offenen und geschlossenen Halbebenen wird jeweils dieselbe Bezsichnung verwendet: offene Halbebene:  , (geschlossene) Halbebene:
, (geschlossene) Halbebene:  . Derr weitere Gebrauch der Sprache kennzeichnet, ob es sich um eine offene oder um die geschlossene Halbene handeln soll. Aus Gründen der Vereinfachung sei vereinbart, dass
. Derr weitere Gebrauch der Sprache kennzeichnet, ob es sich um eine offene oder um die geschlossene Halbene handeln soll. Aus Gründen der Vereinfachung sei vereinbart, dass  bzw.
bzw. 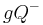 immer die geschlossene Halbebene meint. Soll die offene Halbebene gemeint sein, so ist dieses durch den Zusatz "offen" zu kennzeichnen.
--*m.g.* 21:50, 23. Jun. 2010 (UTC)
immer die geschlossene Halbebene meint. Soll die offene Halbebene gemeint sein, so ist dieses durch den Zusatz "offen" zu kennzeichnen.
--*m.g.* 21:50, 23. Jun. 2010 (UTC)
Die Repräsentantenunabhängigkeit des Referenzpunktes zweier Halbebenen
Repräsentantenunabhängigkeit?
Satz IV.1
- Wenn
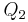 ein Punkt der Halbebene
ein Punkt der Halbebene 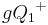 ist, dann gilt
ist, dann gilt 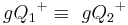 und
und  .
.
- Wenn
Beweis des Satzes IV.1
Neuer Versuch (siehe Diskussionsseite)
Voraussetzung: 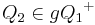
Behauptung: 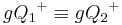 und
und 
Fallunterscheidung:
Fall I 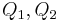 und
und  sind nicht kollinear.
sind nicht kollinear.
Fall II 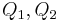 und
und  sind kollinear.
sind kollinear.
Fall I 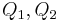 und und  sind nicht kollinear. sind nicht kollinear.
| ||
| Schritt | Aussage | Begründung |
| (1) | 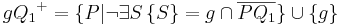 Die Strecke 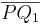 schneidet nicht die Trägergerade g. schneidet nicht die Trägergerade g. |
Definition von Halbebene |
| (2) | 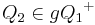 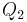 liegt in der Halbebene liegt in der Halbebene 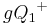 |
Voraussetzung |
| (3) | 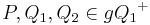 |
Schritt (1) und (2) |
| (4) | Da 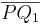 (Def. der Halbebene (Def. der Halbebene 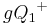 ) und ) und 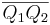 (nach Voraussetzung) keinen Schnittpunkt mit (nach Voraussetzung) keinen Schnittpunkt mit  haben, kann auch haben, kann auch 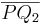 als dritte Seite des Dreiecks als dritte Seite des Dreiecks 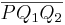 keinen Schnittpunkt mit g haben (da sonst Widerspruch mit Axiom von Pasch). keinen Schnittpunkt mit g haben (da sonst Widerspruch mit Axiom von Pasch).
|
Schritt (3) und Satz von Pasch |
| (5) | 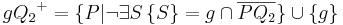 |
Schritt (4) |
| (6) | Es gilt: 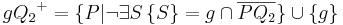 und und
| |
| (7) | 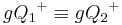 |
Der Definitionsbereich der beiden Halbebene ist identisch - Schritt (6) |
| (8) |  |
Die Mengen 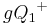 und und 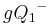 sind disjunkt, gleiches gilt für die Mengen sind disjunkt, gleiches gilt für die Mengen 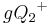 und und 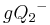 Schritt (7) - Durch Umformung: Schritt (7) - Durch Umformung:
|
Fall II 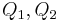 und und  sind kollinear, liegen auf der Geraden sind kollinear, liegen auf der Geraden  . .
| ||
| Schritt | Aussage | Begründung |
| (1) | 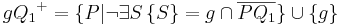 Die Strecke 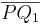 schneidet nicht die Trägergerade g. schneidet nicht die Trägergerade g. |
Definition von Halbebene |
| (2) | 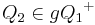 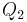 liegt in der Halbebene liegt in der Halbebene 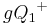 , dadurch gilt: die Strecke , dadurch gilt: die Strecke 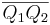 schneidet nicht die Trägergerade g. schneidet nicht die Trägergerade g. |
Voraussetzung und Definition von Halbebene |
| (3) | Wenn 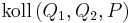 und und 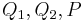 paarweise verschieden sind, dann gilt paarweise verschieden sind, dann gilt
| |
| (4) | Wenn 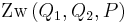 , dann ist , dann ist 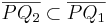 und dadurch gilt und dadurch gilt 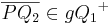
|
Zwischenrelation, Voraussetzung |
| (5) | Wenn 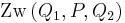 , dann ist , dann ist 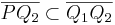 und dadurch gilt und dadurch gilt 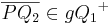
|
Zwischenrelation, Voraussetzung |
| (6) | Wenn 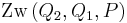 , dann gehören alle Punkte der Strecke , dann gehören alle Punkte der Strecke 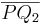 entweder zur Strecke entweder zur Strecke 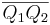 oder zur Strecke oder zur Strecke 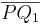 , für die gilt , für die gilt 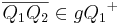 oder oder 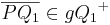
|
Zwischenrelation, Aussagenlogik |
| (7) | Trivial, bzw. analog zu Fall I |
Stimmt das so? Nochmal geändert... --Heinzvaneugen 15:10, 23. Jun. 2010 (UTC)
Analog dazu: Übungsaufgabe 8.1. Dort wird allerdings etwas anders vorgegangen, nämlich dass 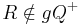 . Die Analogie der Lösungen ergibt sich daraus, dass die Mengen disjunkt sind.
. Die Analogie der Lösungen ergibt sich daraus, dass die Mengen disjunkt sind.
Müssen wir unbedingt unterscheiden, ob einmal kollinear und einmal nichtkollinear!? --TimoRR 08:51, 8. Jul. 2010 (UTC)
Oder geht das auch einfachso wie im folgenden eingescannten Beweise!?

Ich hab ein Problem mit der Voraussetzung: Wenn ich nur sage 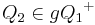 , dann kann
, dann kann 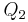 doch immer noch ein Punkt auf g sein, oder sprechen wir von offenen Halbebenen?
Wenn nicht könnte also
doch immer noch ein Punkt auf g sein, oder sprechen wir von offenen Halbebenen?
Wenn nicht könnte also 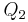 auf g liegen. Der "Referenzpunkt" einer Halbebene darf aber nicht auf der Trägergeraden liegen und so könnte
auf g liegen. Der "Referenzpunkt" einer Halbebene darf aber nicht auf der Trägergeraden liegen und so könnte 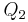 kein "Referenzpunkt" sein...
Hat vielleicht jemand eine Ahnung???
--Principella 22:31, 20. Jul. 2010 (UTC)
kein "Referenzpunkt" sein...
Hat vielleicht jemand eine Ahnung???
--Principella 22:31, 20. Jul. 2010 (UTC)
Ja, mir ist auch aufgefallen, dass es da ein bisschen durcheinander geht.
Ich würde mal behaupten, dass es bei dem oberen Beweisschema (Fall 1) unter Schritt 2 (Voraussetzung, siehe Argument von Principella), Schritt 4 (denn P kann ja auch auf g liegen, dann hat die geschlossene Strecke mit g eben doch einen Schnittpunkt) und in der Begründung von Schritt 8 (auf einmal ist von disjunkten offenen Halbebenen die Rede, dabei wurde in Schritt 1 die Halbebene als geschlossen definiert) zu Problemen kommt.
Mein Vorschlag: Ich würde im gesamten Beweis mit offenen Halbebenen arbeiten. g gehört ja entweder zu beiden oder zu keiner der Halbebenen, hat also für deren Unterscheidung keine Relevanz.
--Barbarossa 07:16, 21. Jul. 2010 (UTC)
Ich find du hast Recht, der Beweis sollte nur mit offenen Halbebenen geführt werden, denn nur so hat das mit de Repräsentanten überhaupt einen Sinn = Repräsentanten sind nur Repräsentanten einer offenen Halbebene, denn wenn sie Repräsentant beider Halbebenen sein könnten (im Fall der geschlossenen Halbebenen) wäre das Ganze ja sowieso quatsch... --Principella 11:08, 21. Jul. 2010 (UTC)
Außerdem sprechen wir bei Referenzpunkten einer Halbebene von Repräsentanten einer Äquivalenzklasse und wie wir gelernt haben, müssen die drei Kriterien einer Klasseneiteilung erfüllt sein, d.h. die Teilmengen müssen auch disjunkt sein, was bei geschlossenen Halbebenen nicht gegeben ist.
Ich zitiere: "Ein Beispiel für eine Klasseneinteilung
Die übliche morgendliche Hektik an der „Maier-Vorwiesener“ Grund- und Hauptschule: Frau Schulze-Mackenroth zog es für heute vor, ihr Burnout-Syndrom mit Tannenzäpfle und Ouzo zu pflegen, weshalb sie sich kurz vor knapp bei Rektor Pollenwein telefonisch krank gemeldet hat. In ihrer Grundschulklasse geht es derweilen drunter und drüber. Xulio-Dävid hat seine überforderte, allein erziehende Mutter ausgetrickst und das Methylphenidat nicht genommen. Jetzt lässt er seine ADHS hemmungslos an seinen Klassenkameraden aus.
Zu Hause bei Lehrer Steiner gab es ein weiteres mal Stress wegen der jungen blonden Referendarin, die Steiner betreut. Er flüchtet deshalb und kommt eine Stunde früher. Erleichtert sieht ihn Rektor Gendarm beim Anmarsch auf die Schule. Aus dem Rektoratsfenster ruft er Steiner zu: „Du musst ganz schnell in die Klasse von Xulio-Dävid. Es brennt mal wieder!“
Damit ist eindeutig geklärt, in welche Klasse Herr Steiner gehen muss. Rein formal hätte Rektor Gendarm natürlich auch die Namen von anderen Schülern nennen können, die mit Xulio-Dävid in dieselbe Klasse gehen. An der klassischen Grund- und Hauptschule geht jeder Schüler in genau eine Klasse. Ihre Klassen sind ein Beispiel dafür, was der Mathematiker unter einer Klasseneinteilung versteht."
Das Ganze ist analog zur Unabhängigkeit des Referenzpunktes zweier OFFENER HALBEBENEN zu sehen... --Principella 20:32, 24. Jul. 2010 (UTC)
Das Axiom von Pasch
- Was Axiomatik ist und wie man Axiome zu formulieren hat, das ist erst gegen Ende des 19. Jh. von Pasch gezeigt worden; von ihm lernten es die italienischen Geometer und lernte es Hilbert.
Hans Freudenthal, Mathematik als pädagogische Aufgabe, Stuttgart 1973, S. 14)
- Was Axiomatik ist und wie man Axiome zu formulieren hat, das ist erst gegen Ende des 19. Jh. von Pasch gezeigt worden; von ihm lernten es die italienischen Geometer und lernte es Hilbert.
Axiom III.2: Das Axiom von Pasch
- Gegeben sei ein Dreieck
 . Ferner sei
. Ferner sei  eine Gerade, die durch keinen der drei Eckpunkte
eine Gerade, die durch keinen der drei Eckpunkte  geht. Wenn
geht. Wenn  eine der drei Seiten des Dreiecks
eine der drei Seiten des Dreiecks  schneidet, dann schneidet
schneidet, dann schneidet  genau eine weitere Seite des Dreiecks
genau eine weitere Seite des Dreiecks  .
.
- Gegeben sei ein Dreieck
Konvexe Punktmengen
Definition IV.3: (konvexe Punktmenge)
- Eine Menge
 von Punkten heißt konvex, wenn mit je zwei Punkten
von Punkten heißt konvex, wenn mit je zwei Punkten  und
und  dieser Menge die gesamte Strecke
dieser Menge die gesamte Strecke  zu
zu  gehört.
gehört.
- Eine Menge
Satz IV.2
- Halbebenen sind konvexe Punktmengen
Beweis von Satz IV.2
trivial (Der Leser überzeuge sich davon)
Satz IV.3
- Der Durchschnitt zweier konvexer Punktmengen ist konvex.
Beweis von Satz IV.3
Es seien  und
und 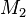 zwei konvexe Mengen.
zwei konvexe Mengen.
zu zeigen: Der Durchschnitt der beiden Mengen  und
und 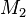 ist auch konvex.
ist auch konvex.
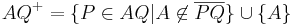
 gehört u.a., dass jede Gerade
gehört u.a., dass jede Gerade 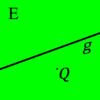
 , die mit
, die mit 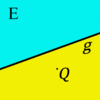
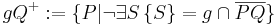
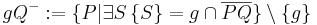
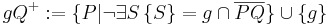
 || Voraussetzung und Schritt (5)
|| Voraussetzung und Schritt (5)


 gilt somit auch
gilt somit auch 

