Zusatzaufgaben 5 (SoSe 13): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(→Definition I.6: (komplanar)) |
|||
| Zeile 17: | Zeile 17: | ||
:Eine Menge von Punkten heißt komplanar, wenn es eine Ebene gibt, die alle Punkte der Menge enthält. Schreibweise: komp(''A'', ''B'', ''C, D, ...'') (analog nkomp(..) für nicht komplanar) | :Eine Menge von Punkten heißt komplanar, wenn es eine Ebene gibt, die alle Punkte der Menge enthält. Schreibweise: komp(''A'', ''B'', ''C, D, ...'') (analog nkomp(..) für nicht komplanar) | ||
*Ist die Frage damit schon beantwortet?--[[Benutzer:Tutorin Anne|Tutorin Anne]] 18:54, 2. Jun. 2013 (CEST) | *Ist die Frage damit schon beantwortet?--[[Benutzer:Tutorin Anne|Tutorin Anne]] 18:54, 2. Jun. 2013 (CEST) | ||
| − | ** Vielen Dank. Ich hoffe ja;-)--[[Benutzer:Blumenkind|Blumenkind]] 16:25, 3. Jun. 2013 (CEST)Blumenkind 16:24, 3. Juni | + | ** Vielen Dank. Ich hoffe ja;-)--[[Benutzer:Blumenkind|Blumenkind]] 16:25, 3. Jun. 2013 (CEST)Blumenkind 16:24, 3. Juni Super! |
[[Kategorie:Einführung_P]] | [[Kategorie:Einführung_P]] | ||
Aktuelle Version vom 5. Juni 2013, 19:52 Uhr
Inhaltsverzeichnis[Verbergen] |
Zusatzaufgabe 5.1
Das Parallelenaxiom lautet wie folgt:
Zu jeder Geraden g und zu jedem nicht auf g liegenden Punkt A gibt es höchstens eine Gerade, die durch A verläuft und zu g parallel ist.
Nutzen Sie dieses Axiom, beim Lösen der folgenden Aufgabe:
Es seien a, b und c drei paarweise verschiedene Geraden in ein und derselben Ebene.
a) Beweisen Sie folgende Implikation durch einen Widerspruchsbeweis: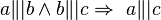 
.
b) Welche Eigenschaft der Relation 
auf der Menge aller Geraden einer Ebene haben Sie hiermit gezeigt?
Lösung von Zusatzaufgabe 5.1_P (SoSe_13)
Frage von Blumenkind
- Kann jemand mir vielleicht sagen was der Unterschied zwischen KOMPLENAR- NICHT KOMPLENAR UND KOLLINEAR und NICHT KOLLINEAR ist? Mit einem Bsp??
Vielen Dank im Voraus;-). Komme jedes Mal durcheinander --Blumenkind 12:34, 28. Mai 2013 (CEST)Blumenkind 28. Mai, 12:34 Uhr
Definition I.2: (kollinear)
- Eine Menge von Punkten heißt kollinear, wenn es eine Gerade gibt, die alle Punkte der Menge enthält.
- Schreibweise: koll(A, B, C, ...) Sollten die Punkte A, B, C einer Menge nicht kollinear sein, so schreibt man:nkoll(A, B, C)
Definition I.6: (komplanar)
- Eine Menge von Punkten heißt komplanar, wenn es eine Ebene gibt, die alle Punkte der Menge enthält. Schreibweise: komp(A, B, C, D, ...) (analog nkomp(..) für nicht komplanar)
- Ist die Frage damit schon beantwortet?--Tutorin Anne 18:54, 2. Jun. 2013 (CEST)
- Vielen Dank. Ich hoffe ja;-)--Blumenkind 16:25, 3. Jun. 2013 (CEST)Blumenkind 16:24, 3. Juni Super!
