Lösung von Zusatzaufgabe 5.1 P (SoSe 13)

Das Parallelenaxiom lautet wie folgt:
Zu jeder Geraden g und zu jedem nicht auf g liegenden Punkt A gibt es höchstens eine Gerade, die durch A verläuft und zu g parallel ist.
Nutzen Sie dieses Axiom, beim Lösen der folgenden Aufgabe:
Es seien a, b und c drei paarweise verschiedene Geraden in ein und derselben Ebene.
a) Beweisen Sie folgende Implikation durch einen Widerspruchsbeweis: 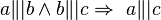$\ a \|| b \wedge b \|| c \Rightarrow \ a \|| c$ .

VSS: aTEILTb und bTEILTc
Beh: aTEILTC
Annahme: aTEILTNICHTc

$||$ - dieses Zeichen heißt parallel zu (das ist eine Relation) und nicht TEILT--Tutorin Anne 18:30, 2. Jun. 2013 (CEST)

BEWEIS:

1. a geschnitten c = {S} -------------------> ANNAHME

2. S ist Element von a und ---------------> (1.)
S ist Element von c

3. a und c sind jeweils parallele Geraden zu b und a und c gehen beide durch S -----------> (1.) (2.)

4. Annahme ist zu verwerfen, da Wiederspruch zum Parallelenaxiom -------------> ( 3.) Def. Parallenaxiom und wenn a durch S parallel zu b ist, dann kann nicht c durch S ebenso parallel zu b sein

---> Behauptung stimmt--Blumenkind 11:37, 31. Mai 2013 (CEST)Blumenkind 11:36, 31. Mai

b) Welche Eigenschaft der Relation $\||$ auf der Menge aller Geraden einer Ebene haben Sie hiermit gezeigt?

---> TRANSITIVITÄT --Blumenkind 11:37, 31. Mai 2013 (CEST)Blumenkind 11:37, 31. Mai

Voraussetzung: 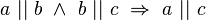$a\ ||\ b\ \wedge\ b\ ||\ c\ \Rightarrow \ a\ ||\ c$
Das gehört nicht in die Vors.: mit 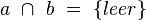$a\ \cap\ b\ =\ \left\{ {leer} \right\}$ \ ,\ \ b\ \cap\ c\ =\ \left\{ {leer} \right\}

Behauptung: 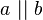$a\ ||\ b\$
Das gehört nicht in die Vors.: 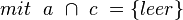$mit\ \ a\ \cap\ c\ =\left\{ {leer} \right\}$

Annahme: 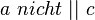$a\ nicht\ ||\ c\$
Das kansnt du dir auch sparen, da du es ja in Schritt 1 nennst: 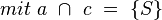$mit\ a\ \cap\ c\ =\ \left\{ {S} \right\}$
--Nolessonlearned 13:34, 16. Jul. 2013 (CEST)

	Beweisschritt	Begründung
1)	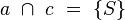$\ a\ \cap\ c\ =\ \left\{ {S} \right\}$	Annahme
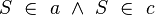
2)	$S\ \in\ a\ \wedge\ S\ \in\ c$	(1); Annahme
3)	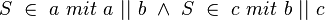$S\ \in\ a\ mit\ a\ ||\ b\ \wedge\ S\ \in\ c\ mit\ b\ ||\ c$	(2); Voraussetzung;
4)	Die Gerade b hat in Bezug zu dem Punkt S zwei zu b parallele Geraden.	(2); (3); Widerspruch zum Parallelenaxiom; Annahme ist zu verwerfen; Behauptung stimmt.

--Nolessonlearned 13:47, 16. Jul. 2013 (CEST)

Ich würde gerne genauer begründet haben, was da jetzt der Widerspruch zum Parallelenaxiom ist. Das habe ich nicht nachvollziehen können. Der Beweis geht aber sicher in die richtige Richtung.--Tutorin Anne 14:36, 16. Jul. 2013 (CEST) Es liegt meiner Meinung nach überhaupt keine Widerspurch vor im Bezug zu Punkt (2) und (3) vor. Deshalb wollte ich eine genaue Begründung.Wo meinst du ist hier genau der Widerspruch? --Tutorin Anne 07:31, 17. Jul. 2013 (CEST)

• Ich habe Schritt 4 verbessert. Wusste nicht wie ich ihn formal korrekt ausdrücken soll.--Nolessonlearned 06:51, 18. Jul. 2013 (CEST)
  

Schritt 4 ist richtig. Das gibt noch keinen Widerspruch, sondern bedeutet das und c identisch sind. Erst wenn du begründest, dass das aber nicht unbedingt der Fall sein muss, hast du den Widerspruch. Zumindest wenn ich es genau nehme. --Tutorin Anne 20:55, 18. Jul. 2013 (CEST)