Serie 7 SoSe 2013: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Aufgabe 7.07) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 7.10) |
||
| (5 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 63: | Zeile 63: | ||
<br /> | <br /> | ||
[[Bild:konvex02.gif|links]]<br /><br /><br /><br /><br /><br /><br /><br /> | [[Bild:konvex02.gif|links]]<br /><br /><br /><br /><br /><br /><br /><br /> | ||
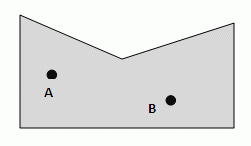
| − | Student XY argumentiert: "Weil <math>\overline{AB} </math> komplett innerhalb der Punktmenge liegt, ist die Figur konvex."<br /> | + | Student XY argumentiert: "Weil <math>\overline{AB} </math> komplett innerhalb der Punktmenge liegt, ist die obige Figur konvex."<br /> |
Wo liegt XYs Denkfehler?<br /> | Wo liegt XYs Denkfehler?<br /> | ||
[[Lösung von Aufgabe 7.07 S SoSe 13]] | [[Lösung von Aufgabe 7.07 S SoSe 13]] | ||
==Aufgabe 7.08== | ==Aufgabe 7.08== | ||
| − | + | Definieren Sie den Begriff Halbkreis. (Kreis sei definiert.) | |
<br /> | <br /> | ||
[[Lösung von Aufgabe 7.08 S SoSe 13]] | [[Lösung von Aufgabe 7.08 S SoSe 13]] | ||
==Aufgabe 7.09== | ==Aufgabe 7.09== | ||
| − | + | Definieren Sie den Begriff Dreieck.<br /> | |
| + | Hinweis: Unter einem Dreieck versteht man seine Seiten.<br /> | ||
[[Lösung von Aufgabe 7.09 S SoSe 13]] | [[Lösung von Aufgabe 7.09 S SoSe 13]] | ||
==Aufgabe 7.10== | ==Aufgabe 7.10== | ||
| + | Definieren Sie den Begriff Viereck.<br /> | ||
| + | Hinweis: Vereinigungsmenge der Seiten | ||
<br /><br /> | <br /><br /> | ||
[[Lösung von Aufgabe 7.10 S SoSe 13]] | [[Lösung von Aufgabe 7.10 S SoSe 13]] | ||
Aktuelle Version vom 8. Juni 2013, 17:38 Uhr
|
Aufgabe 7.01In der Übung vom 07.06. (14 bis 16 Uhr) definierte eine Kommilitonin den Begriff Halbgerade Definition Ü: Halbgerade Wir hatten in der Vorlesung definiert: Definition V: Halbgerade Beweisen Sie:
Lösung von Aufgabe 7.01 S SoSe 13 Aufgabe 7.02Luca aus der 5b erklärt Ihnen: Die Hälfte von einer Ebene ist eine Halbebene. Warum ist diese Begriffserklärung von Luca nicht korrekt?
Aufgabe 7.03Es sei
Aufgabe 7.04Begründen Sie: Aufgabe 7.05Es seien A und B zwei verschiedene Punkte. Welche Ergebnisse erzielen Sie nach den folgenden Mengenoperationen? a) b) c) d) Lösung von Aufgabe 7.05 S SoSe 13 Aufgabe 7.06Beweisen Sie, dass keine Strecke existiert, die zwei Mittelpunkte hat.
Aufgabe 7.07Eine Menge M von Punkten heißt konvex, wenn gilt:  Student XY argumentiert: "Weil Aufgabe 7.08Definieren Sie den Begriff Halbkreis. (Kreis sei definiert.)
Aufgabe 7.09Definieren Sie den Begriff Dreieck. Aufgabe 7.10Definieren Sie den Begriff Viereck. |
wie folgt:
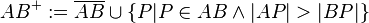
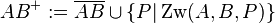
Definition Ü
eine Ebene und 
ein Punkt außerhalb von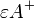 
und Halbraum 
.
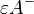, der zu dem Anfangspunkt des Strahls den Abstand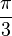 
hat.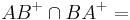
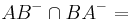
geschnitten mit dem Kreis um 
durch 
=
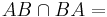
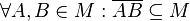
komplett innerhalb der Punktmenge liegt, ist die obige Figur konvex."
