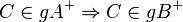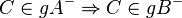Serie 8 SoSe 2013: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Aufgabe 8.09) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 8.01) |
||
| (5 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 8: | Zeile 8: | ||
Wenn der Mathematiker von einer Fahne spricht,<br /> | Wenn der Mathematiker von einer Fahne spricht,<br /> | ||
dann meint er ein Element aus der Menge <math>\mathbb{F}</math>,<br /> | dann meint er ein Element aus der Menge <math>\mathbb{F}</math>,<br /> | ||
| − | die aus allen Tripeln <math>(A | + | die aus allen Tripeln <math>(A| AB| AB,Q^+)</math> mit <br /> |
<math>\operatorname{nKoll}(A, B, Q}</math>besteht. | <math>\operatorname{nKoll}(A, B, Q}</math>besteht. | ||
<br /> | <br /> | ||
# Aus was für drei geometrischen Objekten besteht jede Fahne? | # Aus was für drei geometrischen Objekten besteht jede Fahne? | ||
# Ikonisieren Sie den Begriff der Fahne. | # Ikonisieren Sie den Begriff der Fahne. | ||
| − | # Erläutern Sie wie der Begriff der Fahne auf enaktiver Ebene mit Schülern der SI erarbeitet werden könnte. | + | # Erläutern Sie wie der Begriff der Fahne auf ''enaktiver Ebene'' mit Schülern der SI erarbeitet werden könnte. |
| Zeile 66: | Zeile 66: | ||
==Aufgabe 8.08== | ==Aufgabe 8.08== | ||
Begründen sie, warum die folgenden Implikationen keine Sätze sind:<br /> | Begründen sie, warum die folgenden Implikationen keine Sätze sind:<br /> | ||
| − | Die Vereinigungsmenge zweier konvexer Mengen ist konvex. | + | #Die Vereinigungsmenge zweier konvexer Mengen ist konvex. |
| − | Die Schnittmenge zweier nicht konvexer Mengen ist nicht konvex.<br /> | + | #Die Schnittmenge zweier nicht konvexer Mengen ist nicht konvex.<br /> |
<br /> | <br /> | ||
[[Lösung von Aufgabe 8.08 S SoSe 13]] | [[Lösung von Aufgabe 8.08 S SoSe 13]] | ||
| Zeile 77: | Zeile 77: | ||
==Aufgabe 8.10== | ==Aufgabe 8.10== | ||
| + | Es sei <math>g</math> eine Gerade der Ebene <math>\varepsilon</math>. Ferner seien <math>A, B, C</math> drei nicht kollineare Punkte der Ebene <math>\varepsilon</math>. Keiner dieser drei Punkte möge zu <math>g</math> gehören. Es gelte: <math>B \in gA^+</math>.<br /> | ||
| + | |||
| + | Beweisen Sie:<br /> | ||
| + | #<math>C \in gA^+ \Rightarrow C \in gB^+</math><br /> | ||
| + | #<math>C \in gA^- \Rightarrow C \in gB^-</math> | ||
| + | <br /> | ||
<br /> | <br /> | ||
[[Lösung von Aufgabe 8.10 S SoSe 13]] | [[Lösung von Aufgabe 8.10 S SoSe 13]] | ||
Aktuelle Version vom 16. Juni 2013, 15:22 Uhr
|
Aufgabe 8.01Wenn der Mathematiker von einer Fahne spricht,
Aufgabe 8.02Die Definition des Begriffs entsprechend Aufgabe 8.01 entspricht der üblichen Vorstellung der Mathematiker von einer Fahne. In der Übung am Donnerstag (13.06.) hatte ich den Begriff unzulässig modifiziert. Hier hatten wir den Begriff der Fahne der üblichen Vorstellung einer Fahne angepasst: Gerade mit einer "an ihr befestigten" "Viertelebene". Wir wollen diesen Begriff der ab sofort offiziell als Heidelberger Übungsfahne bezeichnen. Hier eine Ikoniserung des Begriffs Heidelberger Übungsfahne.
Aufgabe 8.03Was haben Halbgeraden und Halbebenen gemeinsam?
Aufgabe 8.04Beweisen Sie mittels eines direkten Beweises: Aufgabe 8.05Beweisen Sie mittels eines indirekten Beweises: Aufgabe 8.06Formulieren Sie die Umkehrung der Implikation aus Aufgabe 8.05 und untersuchen Sie den Wahrheitswert dieser Umkehrung Aufgabe 8.07Es sei Aufgabe 8.08Begründen sie, warum die folgenden Implikationen keine Sätze sind:
Aufgabe 8.09Definieren Sie den Begriff regelmäßiges n-Eck. Aufgabe 8.10Es sei Beweisen Sie:
|
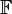 ,
,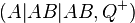 mit
mit 
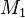 und
und  konvex sind, dann ist auch ihre Schnittmenge konvex.
konvex sind, dann ist auch ihre Schnittmenge konvex. ein konvexes Viereck. Definieren Sie den Begriff Inneres von
ein konvexes Viereck. Definieren Sie den Begriff Inneres von  eine Gerade der Ebene
eine Gerade der Ebene  . Ferner seien
. Ferner seien  drei nicht kollineare Punkte der Ebene
drei nicht kollineare Punkte der Ebene 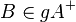 .
.