Auftrag der Woche 4 (WS 16 17): Unterschied zwischen den Versionen
AlanTu (Diskussion | Beiträge) K |
|||
| (7 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | <iframe src=" | + | <iframe src="https://www.ph-heidelberg.de/wp/gieding/Uebungen/Uebung_01/Neuer%20Ordner/Student%20Submissions_007.png" width="720" height="540" frameborder="2"></iframe> |
<br /><br /> | <br /><br /> | ||
Die Lösung ist korrekt, die Skizze aus didaktischer Sicht suboptimal. Generieren Sie mit Geogebra eine dynamische Applikation, die die korrekte Lösung besser als die obige Skizze unterstützt. | Die Lösung ist korrekt, die Skizze aus didaktischer Sicht suboptimal. Generieren Sie mit Geogebra eine dynamische Applikation, die die korrekte Lösung besser als die obige Skizze unterstützt. | ||
<br><hr><br> | <br><hr><br> | ||
| + | |||
| + | [{{fullurl:Auftrag der Woche 4 (WS 16 17)|action=purge}} Seite neu laden, falls GeoGebra nicht lädt] | ||
| + | |||
| + | ===Lösung von AlanTu=== | ||
Wenn man den Haken bei „Spur“ setzt, erscheint nach und nach die Mittelsenkrechte. | Wenn man den Haken bei „Spur“ setzt, erscheint nach und nach die Mittelsenkrechte. | ||
<ggb_applet width="1000" height="900" version="4.0" ggbBase64="UEsDBBQACAgIAOVVcEkAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgICADlVXBJAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbO1aW2/juBV+nv0VhJ5aILZFUjcPnFk4Ayw6aGamRdJi24cuaIm2udatFOXYwf74HpKSLMW5OpntPkwQhxJ5dC7fufBQzuzHXZaiLZeVKPJzB49dB/E8LhKRr86dWi1HkfPjhx9mK16s+EIytCxkxtS542lKkZw7JPJiP0rwKCRRNPKmMR4teIRHLl+6bkxYNOWxg9CuEu/z4gvLeFWymF/Fa56xyyJmygheK1W+n0xubm7GrahxIVeT1Wox3lWJg0DNvDp3mov3wG7w0A015MR18eTnz5eW/UjklWJ5zB2kTajFhx/ezW5EnhQ36EYkan3uRCRw0JqL1RpsioLIQRNNVAIgJY+V2PIKHu3dGptVVjqGjOV6/Z29QmlnjoMSsRUJl+eOO8bTyPdCgn1vGtAgcqmDCil4rhpi3AidtOxmW8FvLF99ZUR6DlJFkS6YZol++w0Rl7joTA/YDgSGILBLrp1zqR2IHTw7+JbGs497ltSzNJ6l8UDHrajEIuXnzpKlFUAo8qUE93X3ldqn3OjTTBzMx2dgUyVugZi6ECcWc5h33TP9CeDj6YXJ0Ejck6pk/UKhrcjAJz2RPjnzaXSGMQ7PppQcySSvkUlbmTjwjs0k/gNmBo+ga3V4jp3Y70ELosyv+RxJpOQFEu396wRqOH4HE2eTNlVmTXagaq1pG08qnlU6X+gU+VMd9hj5kBtBCFHuIzyFISQIsgFhH3k+3OIIBXoMEQ1hwUMURUjTYYpMcvgR/PFCwyxAPjDTsyHkJMIgyEM+RdjklIcgk5DJS8hRQoHC95EPD2nxmGgWNEBeAHc0Qh7oqFMyxEBI4UG4B/EEUYyofhiHiAQo0Pywp1M9iLTqwJKgwEUB1gwhqyGjbTYDfYSotiZo4BJ5WasBRHGWtJeqKDtfADXUo0PZs/VpUBXfzVK24ClsFFfakwhtWaozwghaFrlCrROJnVtJVq5FXF1xpeCpCv3KtuySKb77CairVrahjYu8+pss1McirbO8QiguUrfTuUhx75p0WsMN7S14/QW/txD0rsN75RawguqKg/xCVi05S5JPmuJQGgDJr3m6v5CcbcpCDM2YTcyeM+N1nIpEsPyfEKxaisYFtVuQKVftFhR6tFWkkMnVvoIIRrt/c1lApaLR2J0SGoaRT3EQ6t1qb5c8PxiTaRAFQeAHoetOQbWY6dzz/HHgkQiqPg4wFEKQte8t+X4UhCENpzQIsZXMt52D2I4fbF1Jndi9m0/VRZEepoz5H1mpammaB6iNUhs1z1cpNyFiii3szPFmUeyubGxQy+t6X8KdazVYrAzsCEoD8X0gaMaFHQ2NVq2jcg2NayjcNthE0q3jKTEUZlzY0VBB9FrVGlNxayZ2WzGiMgXNdZq0aYuVjn290de5UJftjRLxpjEV2we+1NmCdxE05InfjqfWGnqOSv3cNHH6+l+96+s1V0x3Iz6h/jQKQx/+kmkU2UC9E6KzDZc5T5uMgGCoi7qyCd5LloTHIoNbu9BAyrS7/wEG2NmEryRvDU9NY2cBN6tuP9iPpg2rn2SRfcq31xBLRwpAdychvkAJvW/Y5RaT2aS1YVbFUpQ6otEC9pgNP8QsIMNgi0r6SasTHJjEhqUSSgP/Vzu3MXOfhVIcqPON5PFa6bpQq3UBcTZPWX5dA1soauA6024WclOtOVfXfKcQWxTbp9mB43VUGG14yjNoFZEyCWJyrAuUuZGgIwIVi1+hMHd7t10/hAcs35ssJq1YWq5NaDSwp2zP5cARht/nIrnrnhZ4qFKl6XQhPkvObWhbjeGiBIamIgzqLHi8QjsrFu1BFT3e2oi1Pbi2VVeJwcZiZ++ECsSvhekJwC7+WICdApfXwOW+EVxxkWUsT1BuOrNLqIcXogJkCukcGgbm6mBDDGsILT61ahcyy7JhdOQBXWI7gLNjBwxrX8/mh1zgnu6AA4wj707YBR2vbktQ0Kxs4ERWmX1LNTuUufiLSBJuGlW7Zf43t49Utk6LrExFLNTjsZnXGZci7my3iIO+daM1HvvBtKl0J8UsHOSOIMPPhKyhq1J9jEWZMG8HIPgzttOMgeOiguZMwVEeCnx+OMpb7ZrmBo4/GmD9CG4Qpwb6pdjxrvOE4iluYZ9hA3tO8cRxTYKzcJdm8j9/In9GE2iSe1y6fDvsHA+lx0ch45TfnxjyKDHixxMD9pme8+MnStMDiQEtne1s9LhoxlPT46TQFyueb03BgC595zYtx95tS1Q7swOMRrbY42bqFvfqF7hNih2at/TzlmpOTORB60qnbvsDcT2njYi513KeQ5M/Ii3Hu1mpzy5iKeITfHzxkI+Tl/g4+e7jx3xMGyffda3XudZ9nWs/5QraZrDjjndj690EBtL1sT0n//0X/Libh12GJj+lZvvYutklr281DjvdF/bFlF0z3trx7RqG50GK74GUvAxSchKk7fGxxdSMf3RMr/hKz9+/zTTADcCUT8Vn1XDsOo0TI/ThruK5UNJnQ/nWfZhBLNU7fRez0CYcH2o3nJf6bcTX/FqyvNLfdwwPlqA9Kw/nTXmKM7UXH2in5VOZcezM03LjuzPfyJkXbWYelzn5i/dSZ3rfnfn/zUxs3Tm/x5n0pc6k3535rZzJd6UEZTXBoe+6KmvpIFhqHDnoJZ56ndY+/+wmHbr7RNjDpv4eoKFm37azU5LF/AiqBx396tdp98BMBjCTF8NMvhHMb9rt/d44DxBbFEXKWd6hwe6+Guq/BH/F68zn15avy2XFlX2RYwz3yWPoDXLXuPuOvZP+a3bzVVnzbx8f/gdQSwcIgJS+GDIIAACTIgAAUEsBAhQAFAAICAgA5VVwSUXM3l0aAAAAGAAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgICADlVXBJgJS+GDIIAACTIgAADAAAAAAAAAAAAAAAAABeAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAAMoIAAAAAA==" showResetIcon = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> | <ggb_applet width="1000" height="900" version="4.0" ggbBase64="UEsDBBQACAgIAOVVcEkAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgICADlVXBJAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbO1aW2/juBV+nv0VhJ5aILZFUjcPnFk4Ayw6aGamRdJi24cuaIm2udatFOXYwf74HpKSLMW5OpntPkwQhxJ5dC7fufBQzuzHXZaiLZeVKPJzB49dB/E8LhKRr86dWi1HkfPjhx9mK16s+EIytCxkxtS542lKkZw7JPJiP0rwKCRRNPKmMR4teIRHLl+6bkxYNOWxg9CuEu/z4gvLeFWymF/Fa56xyyJmygheK1W+n0xubm7GrahxIVeT1Wox3lWJg0DNvDp3mov3wG7w0A015MR18eTnz5eW/UjklWJ5zB2kTajFhx/ezW5EnhQ36EYkan3uRCRw0JqL1RpsioLIQRNNVAIgJY+V2PIKHu3dGptVVjqGjOV6/Z29QmlnjoMSsRUJl+eOO8bTyPdCgn1vGtAgcqmDCil4rhpi3AidtOxmW8FvLF99ZUR6DlJFkS6YZol++w0Rl7joTA/YDgSGILBLrp1zqR2IHTw7+JbGs497ltSzNJ6l8UDHrajEIuXnzpKlFUAo8qUE93X3ldqn3OjTTBzMx2dgUyVugZi6ECcWc5h33TP9CeDj6YXJ0Ejck6pk/UKhrcjAJz2RPjnzaXSGMQ7PppQcySSvkUlbmTjwjs0k/gNmBo+ga3V4jp3Y70ELosyv+RxJpOQFEu396wRqOH4HE2eTNlVmTXagaq1pG08qnlU6X+gU+VMd9hj5kBtBCFHuIzyFISQIsgFhH3k+3OIIBXoMEQ1hwUMURUjTYYpMcvgR/PFCwyxAPjDTsyHkJMIgyEM+RdjklIcgk5DJS8hRQoHC95EPD2nxmGgWNEBeAHc0Qh7oqFMyxEBI4UG4B/EEUYyofhiHiAQo0Pywp1M9iLTqwJKgwEUB1gwhqyGjbTYDfYSotiZo4BJ5WasBRHGWtJeqKDtfADXUo0PZs/VpUBXfzVK24ClsFFfakwhtWaozwghaFrlCrROJnVtJVq5FXF1xpeCpCv3KtuySKb77CairVrahjYu8+pss1McirbO8QiguUrfTuUhx75p0WsMN7S14/QW/txD0rsN75RawguqKg/xCVi05S5JPmuJQGgDJr3m6v5CcbcpCDM2YTcyeM+N1nIpEsPyfEKxaisYFtVuQKVftFhR6tFWkkMnVvoIIRrt/c1lApaLR2J0SGoaRT3EQ6t1qb5c8PxiTaRAFQeAHoetOQbWY6dzz/HHgkQiqPg4wFEKQte8t+X4UhCENpzQIsZXMt52D2I4fbF1Jndi9m0/VRZEepoz5H1mpammaB6iNUhs1z1cpNyFiii3szPFmUeyubGxQy+t6X8KdazVYrAzsCEoD8X0gaMaFHQ2NVq2jcg2NayjcNthE0q3jKTEUZlzY0VBB9FrVGlNxayZ2WzGiMgXNdZq0aYuVjn290de5UJftjRLxpjEV2we+1NmCdxE05InfjqfWGnqOSv3cNHH6+l+96+s1V0x3Iz6h/jQKQx/+kmkU2UC9E6KzDZc5T5uMgGCoi7qyCd5LloTHIoNbu9BAyrS7/wEG2NmEryRvDU9NY2cBN6tuP9iPpg2rn2SRfcq31xBLRwpAdychvkAJvW/Y5RaT2aS1YVbFUpQ6otEC9pgNP8QsIMNgi0r6SasTHJjEhqUSSgP/Vzu3MXOfhVIcqPON5PFa6bpQq3UBcTZPWX5dA1soauA6024WclOtOVfXfKcQWxTbp9mB43VUGG14yjNoFZEyCWJyrAuUuZGgIwIVi1+hMHd7t10/hAcs35ssJq1YWq5NaDSwp2zP5cARht/nIrnrnhZ4qFKl6XQhPkvObWhbjeGiBIamIgzqLHi8QjsrFu1BFT3e2oi1Pbi2VVeJwcZiZ++ECsSvhekJwC7+WICdApfXwOW+EVxxkWUsT1BuOrNLqIcXogJkCukcGgbm6mBDDGsILT61ahcyy7JhdOQBXWI7gLNjBwxrX8/mh1zgnu6AA4wj707YBR2vbktQ0Kxs4ERWmX1LNTuUufiLSBJuGlW7Zf43t49Utk6LrExFLNTjsZnXGZci7my3iIO+daM1HvvBtKl0J8UsHOSOIMPPhKyhq1J9jEWZMG8HIPgzttOMgeOiguZMwVEeCnx+OMpb7ZrmBo4/GmD9CG4Qpwb6pdjxrvOE4iluYZ9hA3tO8cRxTYKzcJdm8j9/In9GE2iSe1y6fDvsHA+lx0ch45TfnxjyKDHixxMD9pme8+MnStMDiQEtne1s9LhoxlPT46TQFyueb03BgC595zYtx95tS1Q7swOMRrbY42bqFvfqF7hNih2at/TzlmpOTORB60qnbvsDcT2njYi513KeQ5M/Ii3Hu1mpzy5iKeITfHzxkI+Tl/g4+e7jx3xMGyffda3XudZ9nWs/5QraZrDjjndj690EBtL1sT0n//0X/Libh12GJj+lZvvYutklr281DjvdF/bFlF0z3trx7RqG50GK74GUvAxSchKk7fGxxdSMf3RMr/hKz9+/zTTADcCUT8Vn1XDsOo0TI/ThruK5UNJnQ/nWfZhBLNU7fRez0CYcH2o3nJf6bcTX/FqyvNLfdwwPlqA9Kw/nTXmKM7UXH2in5VOZcezM03LjuzPfyJkXbWYelzn5i/dSZ3rfnfn/zUxs3Tm/x5n0pc6k3535rZzJd6UEZTXBoe+6KmvpIFhqHDnoJZ56ndY+/+wmHbr7RNjDpv4eoKFm37azU5LF/AiqBx396tdp98BMBjCTF8NMvhHMb9rt/d44DxBbFEXKWd6hwe6+Guq/BH/F68zn15avy2XFlX2RYwz3yWPoDXLXuPuOvZP+a3bzVVnzbx8f/gdQSwcIgJS+GDIIAACTIgAAUEsBAhQAFAAICAgA5VVwSUXM3l0aAAAAGAAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgICADlVXBJgJS+GDIIAACTIgAADAAAAAAAAAAAAAAAAABeAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAAMoIAAAAAA==" showResetIcon = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> | ||
| − | |||
| − | + | ||
| − | + | ====Konstruktionsbeschreibung==== | |
| − | + | Gegeben seien zwei Punkte <math>A</math> und <math>B</math>. Gesucht ist <math>M:=\{Q|\overline{AQ}\cong\overline{QB}\}</math>. | |
| − | + | ||
| − | + | Sei <math>r\in\mathbb{R}</math> fest aber beliebig. | |
| − | + | # Zeichne einen Kreis <math>c_r</math> mit Radius <math>r</math> um <math>A</math> (die Menge der Punkte mit Abstand <math>r</math> von <math>A</math>). | |
| − | + | # Zeichne einen Kreis <math>d_r</math> mit Radius <math>r</math> um <math>B</math> (die Menge der Punkte mit Abstand <math>r</math> von <math>B</math>). | |
| − | + | # Bestimme <math>M_r</math> (die Menge der Punkte mit Abstand <math>r</math> sowohl von <math>A</math> als auch von <math>B</math>) folgendermaßen: | |
| + | ## Falls kein Schnittpunkt von <math>c</math> und <math>d</math>: Es sei <math>M_r=\{\}</math>. | ||
| + | ## Falls ein Schnittpunkt von <math>c</math> und <math>d</math>: Nenne den Schnittpunkt <math>Q</math>, es sei <math>M_r=\{Q\}</math>. | ||
| + | ## Falls zwei Schnittpunkte von <math>c</math> und <math>d</math>: Nenne die beiden Schnittpunkte <math>Q_r^1</math> und <math>Q_r^2</math>, es sei <math>M_r=\{Q_r^1,Q_r^2\}</math>. | ||
| + | |||
| + | <math>M</math> ergibt sich nun aus der Vereinigung aller <math>M_r</math> für <math>r\in\mathbb{R}</math>, also: <math>M = \bigcup\limits_{r\in\mathbb{R}}{M_r}</math> | ||
| + | |||
| + | ====Begründung, warum die Menge genau die Mittelsenkrechte ist==== | ||
| + | |||
| + | Betrachtet man nun <math>r=\frac{\overline{AB}}{2}</math>: <math>Q</math> ist der Mittelpunkt von <math>A</math> und <math>B</math>, da er den selben Abstand von beiden Punkten hat. | ||
| + | |||
| + | Betrachtet man nun <math>r\in\mathbb{R} \wedge r > \overline{QA}</math>: | ||
| + | * Das Viereck <math>AQ_r^1BQ_r^2</math> bildet eine Raute mit Seitenlänge <math>r</math>. | ||
| + | * Da die Diagonalen der Raute sich sowohl halbieren, als auch senkrecht aufeinander stehen, liegen <math>Q_r^1</math> und <math>Q_r^2</math> auf der Mittelsenkrechten von <math>A</math> und <math>B</math>. | ||
| + | * Nach dem Satz des Pythagoras ergibt sich <math>\overline{QQ_r^1} = \overline{QQ_r^2} = \sqrt{r^2 - \overline{QA}^2}</math> und da <math>f(r)=\sqrt{r^2 - \overline{QA}^2}</math> für <math>r > \overline{QA}</math> genau einen Wertebereich von <math>(0,\infty)</math> besitzt, ergibt die Vereinigung aller <math>M_r</math> genau die Mittelsenkrechte von <math>A</math> und <math>B</math> ohne den Mittelpunkt von <math>A</math> und <math>B</math>. | ||
| + | |||
| + | Nimmt man also beide Fälle zusammen ergibt sich genau die komplette Mittelsenkrechte von <math>A</math> und <math>B</math>. | ||
| + | |||
| + | |||
| + | ===Lösung von Tutor Alex=== | ||
<ggb_applet id="NhGHgeYj" width="1890" height="880" border="000000" /> | <ggb_applet id="NhGHgeYj" width="1890" height="880" border="000000" /> | ||
| + | Nachtrag: Falls die GeoGebra Datei hier nicht angezeigt wird, [https://ggbm.at/uFGVcdT3 klicke hier]. | ||
| + | |||
| + | |||
| + | ===2. Lösung von AlanTu=== | ||
| + | <ggb_applet width="900" height="900" version="4.0" ggbBase64="UEsDBBQACAgIAHNacUkAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAgIAHNacUkAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s7VrrbttGFv6dPsVAP4rdwpLmTjKVUzgFig2QNk2cLbq7WARDciSzpkiGpGwp275Tk0foA+SZemaGpCjJ8i12NrsIYJsczpnLuXzfOUN68s1ynqIzXVZJnh0OyAgPkM6iPE6y2eFgUU+H/uCbR19MZjqf6bBUaJqXc1UfDriRTOLDQeCHOvJFNNRx5A25lMHQDzAdChoxjZk3DTgdILSskodZ/oOa66pQkT6OTvRcPc0jVduFT+q6eDgen5+fj9qlRnk5G89m4WhZxQME28yqw0Fz8xCm2xh0zqw4xZiMf/7+qZt+mGRVrbJID5BRYZE8+uLB5DzJ4vwcnSdxfQIKEwy7O9HJ7ASU8kxjbKQKsEihozo50xWM7TWt0vW8GFgxlZn+B+4OpZ0+AxQnZ0msy8MBHpEAC0klYZxhQj3MBygvE53VjTBpFh23003OEn3u5jV3dkkYVOd5GiozJfr1V0QxxejAXIi7ULhI6bqwe4aZu1B34e4inAx3w7kT5U6GOxnOBugsqZIw1YeDqUorsGGSTUvwX9eu6lWq7X6aB2v1yQHoVCVvQJgGECjO6PAc4wPzK+GXY+z07ilJeqvW5eKGi7ZL+j69/pL0Q5ZknZbkAi2p2KOlvMS4bg/XUZOI3pqwlP2xvzsrMnoTd7otXLAil2y9IqP8gPviQIrgQFBvZ03JP4qWk3ELlkmDD1SdGNnGmbWeVwYxLEAiMIFPkAB0SA/iXCASwMWjCPCAiEBcQJP4SJqrh5gHHRwx5CMjRxiy8BA+/OGenUwiAZOZpx6gEhFYiCPBELGo4giwhCwyAaWUgYQQSMAgszyhZgomEZfQYj7isEcDSo+AIIOB0IblKWIEMTOYeIhKJM18hBuwS99sHaakSGIkiZkQcA2YdngGeR8xo41szJVkxaLeMFE0j9vbOi86X4A0MNKa+BxDbfDig0mqQp1Crjg2nkToTKUGFHahaZ7VqHUidc9mpSpOkqg61nUNoyr0izpTT1Wtl9+BdNWubWWjPKt+LPP62zxdzLMKoShPcbfnPCW9e9q7Z7173mkDDdHrkP0Or+nYWDaHDrSoNCyfl1U7VMXxEyPRRTDY8VmWrh6XWp0WebKpxGRsk85EL6I0iROV/QShahYxVkFtDrJ01aYg4XntPvIyPl5VEL9o+U9d5iZZQX6WnieIZJ5PuADQrVyXpN6IBgGjRPqe5D7sLFIGeAEZcRkElFHKiM89AOVqT5dwC+uzzjtqqTt10Kw0qO41nlSP83T9yGr/rSrqRWmLB6CK0uh0lM1SbePDki1k5ug0zJfHLjCYm+vlqoAWdjsIZ9boCHiBCgECzTV0VytjttZJYSuDrQRuIy2Ju34SUCthr6G7WikIXbe1RlXSqklwu0xSWTbDgwYzLVOZwDd5fpEl9dO2USfRaaMqcQN+WMxD3cXP5pzk7uY0u4aSo6p/boo4c/+P3v3LE10rU4wIykTgQxDBXxr4vovTrQidnOoy02mDBwiGRb6oHLp7CI11lMyh6Toakyrj7r+DAu5prGelbhVPbWHnDG57cT/Wdx7bqb4r8/mT7OwlxNLOBqC6KyG+YBMmabju1iaTcavDpIrKpDARjUJIMKd6HbNgGQX5Ke5j1sAbJonslHVSG8MD8Bf1SQ6hdJSq7OUCRgJpwXMD7lTPoZZDtQ1hi4LOlUe2SjQ+Q3n4C/Bml1xd/9qB0H1hONvAV2lxYp3XGCZVK11umMrO930ebxuwNQ3QSGFLUYigQmsXfG7HcFPAhBazG/QLPqnQsomhFWzFXN+4tiuSja4Gxxu8755uORMizJnpCoM9/rQMdhtz8cZc5I7MFeXzucpilNnC6VjPzPPBOpUrbOIMKWKs50yzqNuO0M3WzLFj/KqZrTVveIX5ewrvsz++vfV3Q441Nhx63VwdY9dQSJzCeamyaaVuEoi9+VsSx9oWkS6jvc7ckMrRaDIv0iRK6s5aqXHnk6wGUtUW97tcd6p1YZLUs+xlqbLKHIO3+WZfhFsa60z4/q21MYxdNNrTEYOcTeAgJj3qU94ERpWa8yOaJ6AI/uqP3wdoroxpfNdQYQWFUQ0naeDXbH2Sdv5qSguGjROMRalsTMqtTafJskeDwGzJG+B5tYGw26GQ4N04INeMA3J7H6sy6kFrP/9Z2zWYxiOKhggeoq+gTs3+8v7tXy9C+VrbsKvy9vt+E64vcjjk6y20PnZohUhAihrwbqP28ZeqyKuvL8fuFnE2Q3Yct1lb3DN/rhE8hEoDQ6kBlYZkTAhujoMm/EaeTyUOAi4o9jjUIfdAkrbkvNjoR87mPQtvWP7921fkcrNvoxnkr4nnO4OTKelWoGkSObGmYVw4YkHXDvudMPDJ9F/v36Iv0/prFOA/fj+AyKfw59/2DJSXx+a9XM+/HxuraZqfv9DTVC+t+zYRBiQ+B+3NuelFd6jYIun98fAUNrknY+6JA3V5EBitO/epTyRpDukF2ALIDckFUATMCRD3GPV4AFdfePeTYG/IjY1fhi057pY0Rzcnx6NPjBzlyPfg+G6OX3AUDShv6mtGOVCGDDCTXAr2saixNU9TQ+5JSkB19IbUSD9T4/1RY49W7pobN+NhOxCiG3Bj9F/lxn312uZRYxd1K0ummxhl0p1E6IhTjzLPA+qUAkaJj82b3UFly23KOSzacdjzm3Dl81udwE1KmblL6C736TMK8ARfUexjnwnIacz6DI8CQinkORIw84YUO5cFo8DH1BAOB87xiLxDOv0xT1ezPNt3HLdU+nzHIT8lMF90SpzYayemXpk2g0P4VSVo0SzauqSb7rZxeGN8EmNx8Lcgtz7rXfFaaPvNxOvbEcklG/38cuIiO6vmPPNJWBoAjX0RMA8wTSWQrt8WtIEMBCMU6Bn7Hpe+cwQZScl9bj6OBAHQA/f/b/wSfkp+MQ7Y4xjMMLgDDh8YuFiY785vDFI2/cXvKWfei1+urp+fb75a2K2c393wpcK73ZcKeOQJFvgU6hBfEiEwv37pHOVZnLjXYOZzZSNsCt5ZU/D+T7zMu9MXBJv2D/M81WqdUY+LRbntgf53pw/4PnF9AD6bTitd24zj4NV+Gr4qk17jxHdFgQIReLOz3rvds95WxPIg+ByxHxSxy6KErRijtKX6q/+YQP1tgKDP0tBGQT++qtJvh187r1zsFguW+3ttUpdw+L7kLHBByrFnAWhxLCkn1GOepITeyduUcf/zsP0Pj+bfFR/9CVBLBwhwZstJeQkAAEspAABQSwECFAAUAAgICABzWnFJ1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAgIAHNacUlwZstJeQkAAEspAAAMAAAAAAAAAAAAAAAAAF0AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAEAoAAAAA" showResetIcon = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "true" showToolBar = "true" showToolBarHelp = "false" showAlgebraInput = "true" useBrowserForJS = "false" allowRescaling = "true" /> | ||
| + | Konstruiere nach folgender Konstruktionsanleitung jeweils für jeden Winkel <math>0\leq\alpha<180^\circ</math> jeweils einen Punkt <math>Q</math>: | ||
| + | * Wähle zwei Punkte <math>A'</math> und <math>B'</math> beliebig, sodass gilt: <math>\measuredangle{A'BA} = \measuredangle{BAB'} = \alpha</math>. | ||
| + | * Bestimme den Schnittpunkt <math>Q</math> der Geraden <math>AB'</math> und <math>BA'</math>. | ||
| + | * Die Punkte <math>A</math>, <math>B</math> und <math>Q</math> bilden dann ein gleichschenkliges Dreieck mit Basis <math>AB</math>. | ||
| + | |||
| + | Die Menge aller so konstruierten Punkte <math>Q</math> ist genau <math>M</math>, da es genau dann ein solches gleichschenkliges Dreieck gibt, wenn <math>Q</math> den selben Abstand von <math>A</math> und <math>B</math> hat. | ||
| + | Dass die Menge ebenfalls gleich der Mittelsenkrechten von <math>A</math> und <math>B</math> ist, lässt sich leicht einsehen, wenn man weiß, dass die Höhe über der Basis von gleichschenkligen Dreiecken immer auf der Mittelsenkrechten der Basis liegt. | ||
| + | |||
| + | ===Amerkung Tutor Alex=== | ||
| + | Sehr ausführlich und schön konstruiert ;)<br /> | ||
| + | Am Anfang hatte ich auch das Problem, dass wenn ich nur einen Punkt auf der Mittelsenkrechte "ins Unendliche" animieren lasse, | ||
| + | ich auf einmal auf der gespiegelten Seite wieder ein Schnittpunkt erhalte. Das hängt aber an GeoGebra.<br /> | ||
| + | :<span style="color:#700">Mit dem zweiten Schnittpunkt meinte ich denjenigen, den man sieht, wenn man bei deiner Konstruktion die Elemente <math>f</math>, <math>c</math> und <math>C</math> einblendet. Die Mühe, bis ins Unendliche zu animieren, hab ich mir garnicht mal gemacht ;-).</span> | ||
| + | Nun haben wir 2 bzw. 3 schöne Konstruktionen, jetzt bleibt noch die Frage offen, was wäre aus didaktischer Sicht die sinnvollste und wieso? | ||
| + | :<span style="color:#700">Da würde ich doch ''entschieden'' diplomatisch antworten: Kommt drauf an ;P ! Darauf, was man gerade vermitteln will und wie detailliert man in das Thema einsteigen will. Die erste Konstruktion wäre gut, um zu zeigen, wie man Figuren als Punktmengen begreifen kann und wie Schnittmengen und Vereinigungen damit funktionieren. Deine Variante könnte ich mir als Heranführung an Mittelsenkrechten als geometrische Figur vorstellen, allerdings würde ich sie abwandeln, dass <math>a</math> immer positiv ist, einfach damit niemand auf die Idee kommt, Kreise könnten negative Radien haben. Und die letzte wäre meine Wahl, wenn der Klasse noch nicht bekannt ist, wie man Figuren als Mengen begreift. Aber definitiv ist es ein Minuspunkt für diese Aufgabe, dass man bei 90° diese Lücke hat, die man irgendwie ausklammern muss. Wenn man da nicht aufpasst kommt man echt schnell in Erklärungsnöte, weil man da extrem schnell grenzwertig ;P nah an die Unendlichkeit kommt. Auch da man den Winkel zwischen zwei endlichen Werten wandern lässt (einen der Werte noch dazu ausklammert), aber unendlich viele Punkte als Ergebnis bekommt.</span> | ||
| + | :<span style="color:#700">Alles in allem bin ich immer noch ein Fan meiner ersten Lösung, insbesondere nachdem ich das beim Schreiben der Konstruktionsanleitung nochmal zu Ende gedacht habe. Das wäre eine super Aufgabe, um verschiedene Themen zu rekapitulieren und zu kombinieren, indem man gemeinsam die Konstruktion en détail durchspricht. Man hat da Figuren als Punktmengen, Satz des Pythagoras, Funktionen und deren Definitions- und Wertebereich, Viereckseigenschaften (Haus der Vierecke), Beweisen durch Konstruktion (mit entsprechender Beschreibung) und mit Fallunterscheidung, praktisches Konstruieren von bestimmten Objekten (hier Mittelsenkrechte) mit Zirkel&Lineal.</span> | ||
| + | ::<span style="color:#0000FF"> D'accord ;) Gruß Alex</span>--[[Benutzer:Tutor: Alex|Tutor: Alex]] ([[Benutzer Diskussion:Tutor: Alex|Diskussion]]) 02:45, 19. Nov. 2016 (CET) | ||
| + | Was können die Schülerinnen und Schüler mit solch einer dynamischen Geometriesoftware eigenständig entdecken/erleben/erfahren und somit lernen? | ||
| + | :<span style="color:#700">Sie können die selbe Konstruktion schnell für verschiedene Parameter (Kreisradien, Winkel, …) durchspielen, oder auch die Konstruktion ihrer Klassenkameraden nachvollziehen. Wie man ja hier sieht führen oft viele Wege zum Ziel. Durch die Software merkt man finde ich schneller, wenn man etwas richtig oder falsch macht, wenn die Zwischenergebnisse schon gut aussehen, oder im negativen Fall man nicht weiterkommt. Und zu guter Letzt schleichen sich nicht so schnell Ungenauigkeiten beim Zeichnen oder Rechenfehler ein, wie das beim „von Hand“ konstruieren der Fall sein könnte.</span> | ||
| + | Echt toll! <br /> | ||
| + | :<span style="color:#700">Danke! --[[Benutzer:AlanTu|AlanTu]] ([[Benutzer Diskussion:AlanTu|Diskussion]]) 21:14, 17. Nov. 2016 (CET)</span> | ||
| + | Gruß Alex--[[Benutzer:Tutor: Alex|Tutor: Alex]] ([[Benutzer Diskussion:Tutor: Alex|Diskussion]]) 19:14, 17. Nov. 2016 (CET)<br /> | ||
| + | Nachtrag: Ok, vllt. noch eine kleine Anmerkung: Was ist denn wenn der Fall <math>\alpha=180^\circ</math>, so wie in deiner GeoGebra Datei eintritt? | ||
| + | Dann haben wir ja Parallelen. In der Euklidischen Geometrie schneiden diese sich niemals, aber in der projektiven bzw. affinen Geometrie können sich Parallelen | ||
| + | auch im "unendlich Fernen" schneiden. Also da müssen wir didaktisch etwas tricksen, oder den Wert <math> 180^\circ</math> aus dem Schieberegler nehmen (bei dir also <math>\alpha=90^\circ</math> ). | ||
| + | |||
| − | [[Kategorie: | + | {{WS2016-2017/MAT01/Mathematische Grundlagen Ⅱ: Geometrie/Navigationsleiste Aufgaben}} |
| + | [[Kategorie:Übung 4 (Wintersemester 2016/2017)]] | ||
| + | [[Kategorie:Auftrag der Woche (Wintersemester 2016/2017)]] | ||
Aktuelle Version vom 29. November 2016, 15:19 Uhr
[ www.ph-heidelberg.de is not an authorized iframe site ]
Die Lösung ist korrekt, die Skizze aus didaktischer Sicht suboptimal. Generieren Sie mit Geogebra eine dynamische Applikation, die die korrekte Lösung besser als die obige Skizze unterstützt.
Seite neu laden, falls GeoGebra nicht lädt
Inhaltsverzeichnis |
Lösung von AlanTu
Wenn man den Haken bei „Spur“ setzt, erscheint nach und nach die Mittelsenkrechte.
Konstruktionsbeschreibung
Gegeben seien zwei Punkte  und
und  . Gesucht ist
. Gesucht ist 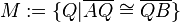 .
.
Sei 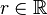 fest aber beliebig.
fest aber beliebig.
- Zeichne einen Kreis
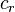 mit Radius
mit Radius  um
um  (die Menge der Punkte mit Abstand
(die Menge der Punkte mit Abstand  von
von  ).
).
- Zeichne einen Kreis
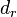 mit Radius
mit Radius  um
um  (die Menge der Punkte mit Abstand
(die Menge der Punkte mit Abstand  von
von  ).
).
- Bestimme
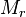 (die Menge der Punkte mit Abstand
(die Menge der Punkte mit Abstand  sowohl von
sowohl von  als auch von
als auch von  ) folgendermaßen:
) folgendermaßen:
- Falls kein Schnittpunkt von
 und
und  : Es sei
: Es sei 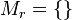 .
.
- Falls ein Schnittpunkt von
 und
und  : Nenne den Schnittpunkt
: Nenne den Schnittpunkt  , es sei
, es sei 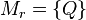 .
.
- Falls zwei Schnittpunkte von
 und
und  : Nenne die beiden Schnittpunkte
: Nenne die beiden Schnittpunkte 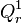 und
und 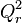 , es sei
, es sei 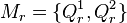 .
.
- Falls kein Schnittpunkt von
 ergibt sich nun aus der Vereinigung aller
ergibt sich nun aus der Vereinigung aller 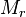 für
für 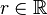 , also:
, also: 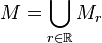
Begründung, warum die Menge genau die Mittelsenkrechte ist
Betrachtet man nun 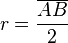 :
:  ist der Mittelpunkt von
ist der Mittelpunkt von  und
und  , da er den selben Abstand von beiden Punkten hat.
, da er den selben Abstand von beiden Punkten hat.
Betrachtet man nun 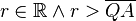 :
:
- Das Viereck
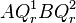 bildet eine Raute mit Seitenlänge
bildet eine Raute mit Seitenlänge  .
.
- Da die Diagonalen der Raute sich sowohl halbieren, als auch senkrecht aufeinander stehen, liegen
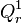 und
und 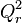 auf der Mittelsenkrechten von
auf der Mittelsenkrechten von  und
und  .
.
- Nach dem Satz des Pythagoras ergibt sich
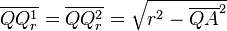 und da
und da 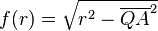 für
für 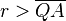 genau einen Wertebereich von
genau einen Wertebereich von 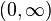 besitzt, ergibt die Vereinigung aller
besitzt, ergibt die Vereinigung aller 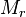 genau die Mittelsenkrechte von
genau die Mittelsenkrechte von  und
und  ohne den Mittelpunkt von
ohne den Mittelpunkt von  und
und  .
.
Nimmt man also beide Fälle zusammen ergibt sich genau die komplette Mittelsenkrechte von  und
und  .
.
Lösung von Tutor Alex
Nachtrag: Falls die GeoGebra Datei hier nicht angezeigt wird, klicke hier.
2. Lösung von AlanTu
Konstruiere nach folgender Konstruktionsanleitung jeweils für jeden Winkel 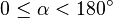 jeweils einen Punkt
jeweils einen Punkt  :
:
- Wähle zwei Punkte
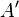 und
und 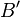 beliebig, sodass gilt:
beliebig, sodass gilt: 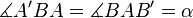 .
.
- Bestimme den Schnittpunkt
 der Geraden
der Geraden 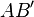 und
und 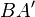 .
.
- Die Punkte
 ,
,  und
und  bilden dann ein gleichschenkliges Dreieck mit Basis
bilden dann ein gleichschenkliges Dreieck mit Basis  .
.
Die Menge aller so konstruierten Punkte  ist genau
ist genau  , da es genau dann ein solches gleichschenkliges Dreieck gibt, wenn
, da es genau dann ein solches gleichschenkliges Dreieck gibt, wenn  den selben Abstand von
den selben Abstand von  und
und  hat.
Dass die Menge ebenfalls gleich der Mittelsenkrechten von
hat.
Dass die Menge ebenfalls gleich der Mittelsenkrechten von  und
und  ist, lässt sich leicht einsehen, wenn man weiß, dass die Höhe über der Basis von gleichschenkligen Dreiecken immer auf der Mittelsenkrechten der Basis liegt.
ist, lässt sich leicht einsehen, wenn man weiß, dass die Höhe über der Basis von gleichschenkligen Dreiecken immer auf der Mittelsenkrechten der Basis liegt.
Amerkung Tutor Alex
Sehr ausführlich und schön konstruiert ;)
Am Anfang hatte ich auch das Problem, dass wenn ich nur einen Punkt auf der Mittelsenkrechte "ins Unendliche" animieren lasse,
ich auf einmal auf der gespiegelten Seite wieder ein Schnittpunkt erhalte. Das hängt aber an GeoGebra.
- Mit dem zweiten Schnittpunkt meinte ich denjenigen, den man sieht, wenn man bei deiner Konstruktion die Elemente
 ,
,  und
und  einblendet. Die Mühe, bis ins Unendliche zu animieren, hab ich mir garnicht mal gemacht ;-).
einblendet. Die Mühe, bis ins Unendliche zu animieren, hab ich mir garnicht mal gemacht ;-).
Nun haben wir 2 bzw. 3 schöne Konstruktionen, jetzt bleibt noch die Frage offen, was wäre aus didaktischer Sicht die sinnvollste und wieso?
- Da würde ich doch entschieden diplomatisch antworten: Kommt drauf an ;P ! Darauf, was man gerade vermitteln will und wie detailliert man in das Thema einsteigen will. Die erste Konstruktion wäre gut, um zu zeigen, wie man Figuren als Punktmengen begreifen kann und wie Schnittmengen und Vereinigungen damit funktionieren. Deine Variante könnte ich mir als Heranführung an Mittelsenkrechten als geometrische Figur vorstellen, allerdings würde ich sie abwandeln, dass
 immer positiv ist, einfach damit niemand auf die Idee kommt, Kreise könnten negative Radien haben. Und die letzte wäre meine Wahl, wenn der Klasse noch nicht bekannt ist, wie man Figuren als Mengen begreift. Aber definitiv ist es ein Minuspunkt für diese Aufgabe, dass man bei 90° diese Lücke hat, die man irgendwie ausklammern muss. Wenn man da nicht aufpasst kommt man echt schnell in Erklärungsnöte, weil man da extrem schnell grenzwertig ;P nah an die Unendlichkeit kommt. Auch da man den Winkel zwischen zwei endlichen Werten wandern lässt (einen der Werte noch dazu ausklammert), aber unendlich viele Punkte als Ergebnis bekommt.
immer positiv ist, einfach damit niemand auf die Idee kommt, Kreise könnten negative Radien haben. Und die letzte wäre meine Wahl, wenn der Klasse noch nicht bekannt ist, wie man Figuren als Mengen begreift. Aber definitiv ist es ein Minuspunkt für diese Aufgabe, dass man bei 90° diese Lücke hat, die man irgendwie ausklammern muss. Wenn man da nicht aufpasst kommt man echt schnell in Erklärungsnöte, weil man da extrem schnell grenzwertig ;P nah an die Unendlichkeit kommt. Auch da man den Winkel zwischen zwei endlichen Werten wandern lässt (einen der Werte noch dazu ausklammert), aber unendlich viele Punkte als Ergebnis bekommt.
- Alles in allem bin ich immer noch ein Fan meiner ersten Lösung, insbesondere nachdem ich das beim Schreiben der Konstruktionsanleitung nochmal zu Ende gedacht habe. Das wäre eine super Aufgabe, um verschiedene Themen zu rekapitulieren und zu kombinieren, indem man gemeinsam die Konstruktion en détail durchspricht. Man hat da Figuren als Punktmengen, Satz des Pythagoras, Funktionen und deren Definitions- und Wertebereich, Viereckseigenschaften (Haus der Vierecke), Beweisen durch Konstruktion (mit entsprechender Beschreibung) und mit Fallunterscheidung, praktisches Konstruieren von bestimmten Objekten (hier Mittelsenkrechte) mit Zirkel&Lineal.
- D'accord ;) Gruß Alex--Tutor: Alex (Diskussion) 02:45, 19. Nov. 2016 (CET)
Was können die Schülerinnen und Schüler mit solch einer dynamischen Geometriesoftware eigenständig entdecken/erleben/erfahren und somit lernen?
- Sie können die selbe Konstruktion schnell für verschiedene Parameter (Kreisradien, Winkel, …) durchspielen, oder auch die Konstruktion ihrer Klassenkameraden nachvollziehen. Wie man ja hier sieht führen oft viele Wege zum Ziel. Durch die Software merkt man finde ich schneller, wenn man etwas richtig oder falsch macht, wenn die Zwischenergebnisse schon gut aussehen, oder im negativen Fall man nicht weiterkommt. Und zu guter Letzt schleichen sich nicht so schnell Ungenauigkeiten beim Zeichnen oder Rechenfehler ein, wie das beim „von Hand“ konstruieren der Fall sein könnte.
Echt toll!
- Danke! --AlanTu (Diskussion) 21:14, 17. Nov. 2016 (CET)
Gruß Alex--Tutor: Alex (Diskussion) 19:14, 17. Nov. 2016 (CET)
Nachtrag: Ok, vllt. noch eine kleine Anmerkung: Was ist denn wenn der Fall 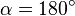 , so wie in deiner GeoGebra Datei eintritt?
Dann haben wir ja Parallelen. In der Euklidischen Geometrie schneiden diese sich niemals, aber in der projektiven bzw. affinen Geometrie können sich Parallelen
auch im "unendlich Fernen" schneiden. Also da müssen wir didaktisch etwas tricksen, oder den Wert
, so wie in deiner GeoGebra Datei eintritt?
Dann haben wir ja Parallelen. In der Euklidischen Geometrie schneiden diese sich niemals, aber in der projektiven bzw. affinen Geometrie können sich Parallelen
auch im "unendlich Fernen" schneiden. Also da müssen wir didaktisch etwas tricksen, oder den Wert 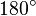 aus dem Schieberegler nehmen (bei dir also
aus dem Schieberegler nehmen (bei dir also 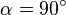 ).
).

