Satz des Thales: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(→Sehnen verschieben) |
(→Umkehrung Satz des Thales) |
||
| (35 dazwischenliegende Versionen von 9 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | = | + | =Ein wenig Didaktik= |
Hier geben Ihnen die Didaktikspezialisten Tipps zum Satz des Thales | Hier geben Ihnen die Didaktikspezialisten Tipps zum Satz des Thales | ||
| − | |||
| − | |||
| − | + | =Satzfindung= | |
| + | ==Induktive Satzfindung== | ||
| + | |||
| + | <ggb_applet width="885" height="512" version="3.2" ggbBase64="UEsDBBQACAAIAINo9TwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3VnNcts2ED43T4HhoZeOaf6IFNVKySjuJdOozsRpOtNLByIhCRV/FAC0Jb9ML30DP0LufqYufkiRkq2KjiexqwvJxXKx+327CxAavlpnKbokjNMiH1mu7ViI5HGR0Hw+skoxO4msVy9fDOekmJMpw2hWsAyLkeXbniXlJX354rshXxRXCKdK5SMlVyNrhlNOLMRXjOCELwgRLTku1zSlmG3Op3+RWPDtgDbyJl+VMItgJcjiLHlLefV4qiZcpVT8TC9pQhhKi3hkhQG4DncfCRM0xunI6jla4o0sb2cQRL4cXRSMXhe5kOpb4zOQIMTpNQFEPCkbnqpAh6SMU5pQnMtglB+ghNAVTcRiZEVRACYJnS/A18B1tLW4KFhyseGCZGj9B2EFuBMGEuiNeQp68omDXzBh4Kih5pMyQy4viBBAC0d4TbaAzRlNWg9v+Osi3YpWBc3FGV6JkilOfSO6EBs5AczFpMPjfJ4SI/MA8gWJl9NifaFB8LXpD5uVekU5NJ2fFWnBEJMRQOBzc53qq9KRntZajtJxlIaxIY3W4+7AUxrqOtVXpZXSXLtmInerqCuI8ZpyJAUSRkjFOvgUTwlQa6Eyp+Jt9QApsDShuvqFX8tsCjXQTILapvtYNoenO+kzXBKWk1QnSQ7clkXJ0aVMRj2XciQhMc3gUQ8YSLCk6zdwQEsTMmekclxXkAZMjbYScUc8PK2ckD5w8DUW0AogHiFjkZUqoErkXYKFlCjNLMN5gnKcgeRNLiBOqGJLzkJl5SLsjKz1GCAEA+7I2qhb5UVRikphoh0w1mR5pSQjUHtC5ZlK0xrviVU3mkL1jKo7mPEtczBc51TYUyklL1N9welqgSH4qq5SvIEW0sRJGTyfzTgRaD2yTtwQ6hHaidsYnhTJHeByqa/rF95TN9e6qSodXXeyY6g3fZMUOug9WN+p8O+CdBfH13+6XZCU6ntYtpP7bjBdT5e5upoy746nO1DwuN4hOHEOOa8SEfrmSpqXVbUiJDGLlDCtCK1gQtXYGiWzJcO3ZTPZGFYeTsYZZXFKdtiY6OQ28LcoWR4mBEqNxjXaS6vd5cQCmklOOFetWDSbbtf8b/fcByR/qOE78Q+xdZTrsC6S/BIcLxhHaO0YIjdORU4lWbtV8WxcI7p2G8xBYjC6RuNKf1xpjT1ZrYHth6E/2P5gwDdzjHuV6XHQgIF8yrX7XHdwSLSYzoChzgW63MuEsy6lefagJvc4delrog92uccqS88OI9fpDTwv8Nxe5Ho9NblnR8GgHwVRz/G8gev3vqRkL8hcyncIksWqqvZsj6npYaa4sVdxMX2Mqm2g8+Vle2BROrkDWsW27fnRIHD6/R4MulE/1JCD3HX8ECjyw0HkOb0uhb5TTTSDzXpMRQ14KjOj3jVANu1vepaErORu8zz/wHDO5VeH1mlspu7h/T3e3Mf5ZI9zfJhzBrYqqvAD+T5mZX10vutNiF4Ar03bezYk3renXGoi8f4eSA+MO22EvtWW0tXkBMdx+fA9zKHgx99sP+3r6KMjO1cd/pduqO9eEMb3LQdxt+Ug/h8sB6EdOq1lWXeO57waHCT9rp170o325FnRXi0LfTvSe6tntSioM6r7yhdhT3b0XTpvbw7zqQ5SaiJAW74P/pQGQ9cO+k5/EPpe2B/0okEYPuxDrDoi22cz6MbmUURhFm/bYlAJ07S4ek9mKVkrJPeoIRm4JE8039cngjs6rcVlvWIwufwYMJF/IGsBOy0YGFnffyoL8ZNro4+QC/GCkilBCcnRuzJfCnSGcDmD5wz9wgjlttZWM7TpEWDSatv/ep/Be9hzgZlQn31IllNge6HT+LnmI2YQNpep/8bMa2Hm2WhCOUcZFQqh32m+JGkGr4GPCeZogj//DSPcjHB0e9MBQO+JAWgwCzpi5rcw820AgySELQrI2YQSBFknIN2urwhFF/GCUSEIysiCzXC86ACX/zThcvuD5q/fDbxeC7wegAdpNfv8T5pCylEmi/PV8RD1nhZE0X5JunYbrkHUDa+ghVezIH88HqbgScHkO/swOXbHPAoNLrc36AekkTB4oCMACY8GJC7yhOpjJ9A+N8pfDS29W9IAebu43YNXK/RpAW0J53VkZHeX0ViEv/YJb2jO4z3n4IF8jFeKACW7vRntBnza/PdI/WFq/jF++S9QSwcIZehO1mUGAABjHgAAUEsBAhQAFAAIAAgAg2j1PGXoTtZlBgAAYx4AAAwAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAQABADoAAACfBgAAAAA=" framePossible = "false" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" allowRescaling = "true" /> --[[Benutzer:Gubbel|Gubbel]] 12:10, 21. Jul. 2010 (UTC) | ||
==Funktionale Betrachtung== | ==Funktionale Betrachtung== | ||
| − | |||
| − | == | + | ===Variante 1=== |
| − | <ggb_applet width=" | + | <ggb_applet width="1005" height="544" version="3.2" ggbBase64="UEsDBBQACAAIAAO77zwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3Vvdbts4Fr7eeQrCCxQt0KgiRf21SQs7SbvFtttF050Ce7OQZVpWI0seiUqcvMzczAs0nZkXyH2eaQ9JyZYsx7Vst00mF5FFUeTh953vHOpY3n8xHUfojKVZmMQHHazpHcRiPxmEcXDQyflwz+m8eP7TfsCSgPVTDw2TdOzxg46hkY5oz8PnP/1tPxsl58iLZJefQ3Z+0Bl6UcY6KJukzBtkI8Z4rd3Lp2EUeunFu/4n5vNsfkEN8jqe5DALT3No88eDN2FWnj6RE06ikB+FZ+GApShK/IOOZYLp8OlnlvLQ96KDDtVVCznokIWL0GSIq6MkDS+TmIvu88GH0IJQFl4yQISItv0ncqH7LPejcBB6sViMtAM6IXQeDvgI+uq6CWOyMBiBsSYlajg/SdLByUXG2RhN/8vSBOzBpkD6Qp0ZlIqzDAyDGU1dXqqeyWHY2QnjHHjJkDdlc8SCNBzUTl5nvSSaN02SMOaH3oTnqSTVKJpO+IWYAOZKhcHdOIhY0UYA8xHzT/vJ9EShYKihP1xM5C3SoH5wmERJilKBLyw8KI59dZR9hKWzXrrso8sexRhi0Nl17BLZQx776ih7RWGsTCtWjstVY72cJsyQaBAwgi/OFh95fQbcdlAeh/xNeQI+cFosFasb/pWP+yCCqhfMxsS7GnP/yYL/7J+yNGaRcpIYuM2TPENnwhvVXNKQAfPDMZyqC+WKBV3/AQNU64AFKSsNVxJSgFXvUY640Lz/pDRC2JCBrT6HWADr4WItL/P4VJyDM6Ie46nnj3geB0jors9AfjHyYjiB48cwPmWR0DYHXQlMBh6HIUScYBEbM1AVlw4k/W8G5NvOLIQkMhqUui+uzymBy0udSbqdF01GHrSUeom8C7Cxun453ttkwBaQBHTlkkGhEzGA4G/C2KCIh7xwejSBIaWEKuRITDM0Pejs6ZpBQbjiLvHhUt0ueynBiVghZzYKb1CgfAWe3v9wE6C6K94ThLDmOHr1D0u49rBmknZ4+cl4DG6HYm8MEx+GqR8xCVIo8gbydOFVyMMKPYVMzstLvhquGKQBP8gg9GfY+p16BOIjEHrMskyGSV4NiLe7cAWO2xjSN+dnLeMgK7H4DExL0gyhqV5Qd6GrCdFl2TLF0pfFNVw0XeIKN+AKaThF3bJ/t+zVJYJLrGHXqtAMftc1ijm6VHwQ4uiaknf4qIz7JVYLyFQEBefyw2Hor+b931Inddr9Btvd1WzXxdbdIhaZeHupDcMpG6iW+VSVGGNorqVT1ya6QYnhWGQWcGrCMreR0xtwpwVUu0pMbxvgeqvBFZ45w87bUEltY90WSpojTTVKdccluuuYum4R63gPWxJsQ7PIAgWA9R7VHBNTyyImMR3btc022lxw/3AM21s/5Kt5eh1z2F4ARA0JSLI8OIitb4lBhbVeG0n07rYk4EHEWaoIw63+tUzImwSawzaoHv5gVHeX03UHW5aNiWtg13YstQWimmW5lkt1y9INh1Jrq4h0wgLRvsDAofLzboOI/moismK0Eur+3c/wVXc3SBVY01F7KHiepARb1DCITQ2LOgpvV3OpYVNKKLFsB+jZUVSSeEfCL2ZRCHyp+exyythEPDS+iz+kXpyJ6kFdym1J791G+qAd6YP7RDrslDDWCTF0QiHBYNMyIR2ZinlbI1SHAAcu4VDbJirSuZqtgySJqZvYNt1dZaMfxnsh9l6Dd9aOd3afeF8Uuy0ZJ7DDdhxD122KdarbltqAYENzoK8DesfYNS18jziXxafbwrvcxjSJv/m8mnlZIZlRBr3F/WBPXqBtapbrmia1MCaOS037a6wvT8ll6atJu2GuyTteQZSxQJSX+vO06ZaNUZScv2fDiE0lkg1q2BhsErXK97NS30KfjbjpKW6awfjmqhU3V4vc6Jrr2NgyLUN3dWpbtrEZOUqRWG+SQ+8pN6v2lEd3uU609o6SarOy0C7LaMd/LXCIZjjbbKnfJ9zji7I+UrLee3jz+ZGS9nFD2kcPvEmSPWvzrFPeshEB4oEiUIe+Ouzi4R4iii6ivyiWOKY7q0Nigk14iITHd/HMv9VDy7K4WSIhYT5WEB81o+cXVbRcO35+KUrEtQhqOgaET8s1HVeHpzO8fgT1k3gQKleF3u+Kzqdtct+64bXxBc+64dX8HqlvuUiqHIJUrr4mlY0Fc9dkY2qYzqNPreBofCOlLNPLHM+6an5vpZnfv7rncL6BYrbfkNxtxSypHR+V7C0SNlzNV612PLxPtWOQQb34qGo06msWWSomVq3Djh7UWtFyrGhpxKgaRUELioL7RNHt5X0gT+06iUZtE89Jsuk3p2lZnXnYIOVlm1TycrP0gYnK7PJ4x7a++pZb32UoBw2UX7VB+dVfBmVLw2R5jse7r+C/vC01jNoV9Ua7KOptnM13GJaI/Nq9kiocbVW+v2NVvOUkF4nmVYPksB3J4Y4rtz+OZUdzHGw7FLs2yIqYZJZ8gH+y5It8qjm6bVZS0V32CTadpGCJALYA/QObcogecOGg8+CXPOHPxtd/BpGGuvkwgC4xBKwoyuPg6YO/Y/2Z/Ndj5yxg6BB5+RAN2Bj9M2VhpslrH70MTTyYgqUcjUOObj6jHLzwvNoOu9bQH10yoDhQna5eqMmlwXVf42Bhp27u5uXGrT0l417KZZZCKvHpagNpapTcGpG/TgGpUfCRxTHA2xc4c3QepoPH4j3g69/E23ygCQCvxPXmSkMS+OOYnzPx5h9cEHegIL3+8/pXaFDdVOMpIB+z9DFKRNd8HLBTNkq5Nic3YLGXs/SpGAey1pijcIwyFoEroLfe9a/oMn8MYzExpNdXPcQMlbHWZpKszeTygPDpe9FsaWZD+/J1E2q149mo8XwEMJ7k4zEDJWXytc1XijR0BrcVDDearxThYSaoGcNVJScNPRzAeEdeWkoWbufAWsr8Ec/AmzJ+/RsojiPol2mP5CjdKEvQOM8yMAG8SoxQm+yLeJMUfPFUvH/qARwZOJByl4ev45jF5/LN0kyuYtGkZ6jHxOwxGAOGCKX/I4yGTN4u1tUYgaUBE55WtWPAsuL91UwZ82h9DzO29LBvl3IaHmbRhfihXpWpuV29ltOuavOyVqlppvybP1rVaP5YrNFQzcbEcBzXEd+HWo57Bzd1GxdoRFXo21doltFWvN53eOtXrV/alaMXacOaaeu2axnEsl3quFaL0tqarz/hdspYa+tUY8f4Ht/n9ZMkYl48g+HTIpKVeb7P5uTdcJgxLrchZYHENFch63sTqTLZ1mNJv/jFAIuftlv76Z1ae/HqhWWsvfYTfxRBzhsmUcBSsbldXP6T6u8t5G+Mih9ZPf8/UEsHCFrfzszPCQAAljUAAFBLAQIUABQACAAIAAO77zxa387MzwkAAJY1AAAMAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYS54bWxQSwUGAAAAAAEAAQA6AAAACQoAAAAA" framePossible = "false" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" allowRescaling = "true" />--[[Benutzer:"chris"07|"chris"07]] 21:47, 15. Jul. 2010 (UTC) |
| − | |||
| − | |||
| − | = | + | ===Variante 2=== |
| − | + | ||
| − | + | ||
| − | + | ||
| + | <ggb_applet width="884" height="510" version="3.2" ggbBase64="UEsDBBQACAAIAIi17jwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3VnLcts2FF03X4FRZzrtTEyDb7KR4pHtpJNp0mTiNJnppgORVxJqilRA0Jb8M930B7rJqjvv+029AEi9rVh+tHHlBc2L173nnHsBSO2DySgjZyBKXuSdlm3RFoE8KVKeDzqtSvb3otbB00ftARQD6AlG+oUYMdlpuZbTUvaKP330VbscFueEZbrLew7nnVafZSW0SDkWwNJyCCCX7Kya8IwzMX3d+w0SWc4bzCQv8nGFq0hRoS0ZpS952bzuqwX7RS4JKfkFoNOOsrX3tS9tqJKMp5zlaj3tG3Yi5JyncthpRZHXIkPggyFO59PIzJYUhUhPpqWEEZn8AqLotGINxdS8OLGn3sqEZaCG6abFNz0LnJ2AlAhcSdgE5iENBE+XXl6Uh0U2N40LnssjNpaV0Ki7telETtUCuJZQ/nbzQQa1zUFQhpCc9orJicHANVO/m471EO1Qb3BUZIUgAgf4Pnaonz3z1H2Up7NeVPehukc9h5p01m7Hju6hnz3z1L0ynhvX6sjtJmqbNsvwkiiDghHFMgs+Yz3IOq0WqXIuXzYvkiendai2GfBTNeqhShc1MJvTvqs52/sr6mmfgsghMxrJkduqqEpyxrJmLe1ICgkf4atpaCJWdP2MDhhrCgMBjeNG4wawxTFGhyvm9n7jhPKhRF8TicmK8UgVywmTF32ep1U+IM+r/FS1oTDJIUjBkqFUdqYSTg4LoXBImcRhKnkhgxFgHkktGq25GXivWrO8LnSKNslYt89pwOaNAtJSY9l4yNDS5EjGpiCWYtbzvSpSWEEPEdVhYlKO1QSKszFAWhcpWQudjHFKnTYLhGgcSzJRfcMIcxW9sShq9sKM1p1MjqnioBd2awEYTD6DzuGv9jo+y+pbcOdeEOrzCaTGMudiHrhv0Vngu8WdFKMRy1OSsxHGfcRFkoEOlquaTBhV4iDMNiiYACvZNCXG1t6vp1kDEjXMkxlKSQ3kvIDIIeZpDmWpq5xcrGdXq/EaYNObQ30t53BPgfwMXStESciE1jqdUrMguWgsE0Ruz2whdm26sBf4Qd0LPiHdpn+36dV1cKBrBZ7tx/MPSqjr1mt0PexhJN/18V8teuPdx9xEUJoKiKmU8D4SsZX8N1r0y9wnG0jvbqd8OXe6N6ostmM2MP38UqoLYu1FNI5o5IaeHYSxH+ucsy3fdgM38JEpJ6ZBvGPpuRkLx7uwcHzD+vVF8qAkTxc/jqYB6XHQHuCf71OPRkFwGx5eYhnYXAiP17hgnyuDqqbMsGY3roI77zm3KINzvF3Lpau46q3GcajnBdSLHZ+6tvtszzaI7/lWhBlCwygMwzh0Qn+XyrpSu/honPGEy+1sveJCFGKFr67hi23InsNdsufwv69hS1u9t1iEws01KLyN9k9goOyb4TxcPwVsB7OsZ5udAu7iDLAZ8+bic4fq3/MsD0UfOwi6j2ngBEbnCHpg+Y4dB8iCF7muH7tG/TGq347C2PWQjoi64R2pX2OeqcL4Ipd4kwF9M1i/oJwCjNXN8HX+TrC8VHf45ZPj1cTPJt6wAV2ZS89M0/NdUurZDTekwNP8qkfPPG7P8H3tJ9vif/5lxR/Gix9zlfAt11kK/9841RztIqKjW9xaberctkZ85k7mWFiKaeh7kedj6QipX8Pq2JEfubhj2qEb3wrVt2y6gumRycXuGrDpdmAFztTAlj6w00mIJxBVan3H86LYNsnrWTR0qR+4eEixfTeo90PbCnyHRrYfunaImR48nNp8JdnrGzJcn2x40GRTrz6K6hff9Z3IjhynPoY6juXixmwHse/iecnzo4fDtv7+d4Xv1PANa3z//ed2wvW3kzOysLcaj45UNc54sVWHmJDGTuDZjtMAddPSus64d03G175hXmDIW2GIiWReKYPGmGXF+VvoZzDREK5wcsMz79Ea5L3dzry9+zvz3nmS7W0uqZsr6t5DLqmbOb+yrLLdOGcPiPP/c2GFyVigJ+qLpxrUdzCRKGps6LS++VgV8sno8tMgs0i36g+wS15KyLIqH3z/zdc2ffIePUmGHHpAUg7kBLgEkjwmPE9hRNKKpJCTN+rXGNIlrOoTZf5RAC9JD85hUEpLz/MBB5+BGF7+kUlS8mRIUlyMY3dBBuLyrxzIB56fQnZgurM8J0MmCTardX8Ql58ufwcS0wOiO3x7XAmc5ByyZDjzYFSV5aKbZADY+BiXGnG5vhQBnpO3kAwR7sbES3nwncFFY7ksc4ngtZaR3C7h+z0clJIJqa8XpP6S1vWWbnN+c5uL3KVbjrd48l7Uy/7iD2/6p+b65/Cn/wBQSwcIfLrPecUGAABAHwAAUEsBAhQAFAAIAAgAiLXuPHy6z3nFBgAAQB8AAAwAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAQABADoAAAD/BgAAAAA=" framePossible = "false" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" allowRescaling = "true" /> | ||
| + | --[[Benutzer:"chris"07|"chris"07]] 21:12, 14. Jul. 2010 (UTC) | ||
| − | |||
| − | |||
| − | = | + | ===Variante 3=== |
| + | <ggb_applet width="884" height="510" version="3.2" ggbBase64="UEsDBBQACAAIAHW27jwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s1VnNcts2ED43T4FhZ3qqafBXZCMlo6jTjqdJk6nTZCaXDkRCEmoIVEDQlvwyvfQFesmpN9/7TF0ApERKthLZzoytC80FsNj9vt3FEu4/X845OqeyZIUYOJ6LHURFVuRMTAdOpSZHifP82ZP+lBZTOpYETQo5J2rgBK7vaHnFnj35pl/OigtEuJnyjtGLgTMhvKQOKheSkrycUao6clItGWdErl6P/6SZKjcDVsmJWFSwi5IVyLJ5/pKVzeux2XDBmfqRnbOcSsSLbODEEZgOf72jUrGM8IETYivxB46/NQiiQI/OCskuC6H09I3yCUgQKtklBUR8LesfG0f7tMo4yxkR2hljB0xC6ILlajZwkiQElZRNZ2BrhBOrLSsKmZ+uSkXnaPmBygKUhpEGemXfgrCn30qwi+p1Zqj9ZtTQ81OqFNBSIrKkG8CmkuWdl5PyRcE3okXBhBqRhaqk4TSoRadqpTeAvaQ2eCimnNYyHyCf0exsXCxPLQiBVf12tTBLjEHj6ajghURSwxvBhPo5tk8zR1u6noXNHGxm1Dq00vW4l/pmhnmO7dPM4kxY02rPvcZrDzfbsBJpgYYRQnHtPCdjCtQ6qBJMvWxeIATOalc9u+DXaj6GHGgHwVqnd186+8db4dM/o1JQboNEALdVUZXoXAej3csYktOMzeHVDjQea7p+BwOsNKdTSRvDbQZZwNprbCBuifvHjRHahhJszRSUAvBHaV9+qsSZfodgRC+okiSbqUpM0Rst12UjmzE6BolOaQXppLHIiYKlujxQTucUkkmZwDFxtwbwlbOuHIUpAk261+MbKmD42iAy4Ub4YkZA0uQJJysoCW2/jb5XRd5FY8KWNLeSzU4GohIttb40gTTUJTGIHXRpa6OZZNNHJ75ZHdTcWlc/4/SLB+104Kahcdp3oe4d5HRWzOdE5EiQOTg9YjLj1PjKdCVHBGvCEfE0BNa/SjUDmVVWq9hBEOKSZWuEMqdbEtQMMk/QsjR1S7Ur1M0wt9LrJpzx7VH+IuPgmKDiHEwrZInQEteH7wrbDdFlI1kCZkf2UPBq0aXXYgaOY8mWaNjMHzazhnDKHcVu5Kc+Xv+gOA2DeothaDTrQB9G8KcJdWvcR2EdKG1JKxdQhCYs28/6S/D7Szkn+znXEK7ZIrekvFuwvy7nmyQCRHtxnUWpLR1H0C0lONmwgONDImWLDDaH5idjaj8ZJ0JBeQYcthjJLCMEHroxavxsUTPcT023oA0fdEGDkE7bsGPsG2awG3ekOi1uX+1O6VTLt4Ae3hT64/34lrW2BsHxwy94HcAjC3HkpvYI0SUo9u4r4A2SfAWt7DrAoT3Z7ZrOKF3odvW1eCuJKPVnSzdMbqbzjQnw7azZZnH0h3dInujptytQnm+ba/O8a74QAb2kafDge2ShFehudUGpbXQbGtACFJrPhZZRG5Y910+jBPfiXuqlkefbche6QZrGYZJ6vh8FOEnvklPXnCUaQpNSr3bIyA84TfJHdZoELg7aoCa2K4VDJvA6FNgKduS7UZgGUS9McYD9OPr6B8116ZLvpstByXKrQ6X5Cr0z+veXJMAC7nm9CAe9KAzXWYKBsxBHaS+Ig+j+T56RTZPhDgn0sJOHPqaTJ3B7XVwDmyjQevU6NCQG8NQNeziNcRKFQYBxtHPV8HDPp72k77Ybk8NInzwm0n0g9xrSfTcOI5ymfuKHaeyHUd2Ge6EbRRAFfhokoZ948SNi3VzQXd9ijmwvv0v9f//s597cIq1Jg9l6PdhT1XhDM9cLkjgI4QMyDuKw53+O+H3tvod3mQ+/kPl9RAVbRBGZbQpo1Ag5Ly5+oxNOlwbJLWo69zfLhQTFuv7XXr2lSwWFHwYGzncfq0I9nV99mnIXDavJFKYIOCc4r8T0h+++9fDTd829GEU5FfauDI0QE0jfVn+gLJsJmOyaye9JiSZXf3OuUM4kGlNmZv0srz5d/aUVlGgqr/4VoOg9E2eUl4hUk++RWXxBhUAj17WqjmAE1sgZ4WOz8BdJWQnPepTN0YkQVFLRHl0vnYB0bqVGhjijU/XcOmxA6kaPAlScLkR3/Ra8Q1EoFZHK9CJIV4YQ6nva/kX16Rt3bvPavB+3L0DNnX/9T49n/wNQSwcIe7Bi8UEGAAAmGQAAUEsBAhQAFAAIAAgAdbbuPHuwYvFBBgAAJhkAAAwAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAQABADoAAAB7BgAAAAA=" framePossible = "false" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" allowRescaling = "true" /> | ||
| + | --[[Benutzer:"chris"07|"chris"07]] 21:12, 14. Jul. 2010 (UTC) | ||
| − | + | =Beweisfindung= | |
| − | + | ||
| − | + | ==ikonisches/halbikonisches Beweisen== | |
| − | + | ||
| − | = | + | <ggb_applet width="1080" height="620" version="3.2" ggbBase64="UEsDBBQACAAIANOV7zwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s7V1Jc9s4Fj5P/wqUpqorOYjBxq1jd5fjbO44k6k401M1lxRFwRJjilRIytuf6cv8gd7S6833/k3zAJCyKFKyKFm27OlcZIEgCLzvfW8BHpWtr04HIToWSRrE0XaLGLiFROTH3SDqbbdG2WHbaX315WdbPRH3RCfx0GGcDLxsu8UM2pLto+DLz/62lfbjE+SFqss3gTjZbh16YSpaKB0mwuumfSGyUrs3Og3CwEvO3nQ+CD9LLy/oQfai4QiekiUjaPMH3f0gLb4+Ug8chkH2NDgOuiJBYexvtywTpg5/fSOSLPC9cLvFsW6hsC7HLV2EJiav9uMkOI+jTHa/HPwQWhBKg3MBd1LZtvVILXRLjPww6AZeJBej5gGdEDoJulkf+mJHjimCXh8maxFHD+fHcdI9OEszMUCn/xFJvN2ihEtJn+lvTH9LYWLwRBOrS5Pf1DDi+EBkGeCSIu9UXEqslwTd0pe99EkcXjYN4yDKdr1hNkoUqCxvOsjO5APgWYmc8E7UC0XeRkHmfeEfdeLTAy0Fpod+dzZUt6gJdXq7cRgnKIEbTBM65J8d/an6yJmOe2HVB6se+Rhy0PF14lLVQ3129KfqFQaRnlq+clKsmuDiMUGKZIMUI+jiePGh1xGAbQuNoiDbL76ADhzlSyX6hn+MBh0gwaQWjMck1zXm1qMp/dk6EkkkQq0kEWA7ikcpOpbaqJ+lJtIVfjCAr/pCLhJPwvUvmIBu7YpeIoqJawppgamreFIRp5q3HhWTkHNIYa5+BrYA1pPJtTwRJyJID4OoO4p6sOIuylsu/ugn0CSpnAGNpAi6XgZ3SLMgQjEQQKJM6YtSt7HcXrfGFiNW5C9onl+/RAAu1+qO0jIvHPY9aCnoEXpnYAoml6vGex13y0I4DE5FV7dcPklJJkWn2602NpgF9JO20HZa6FwbRdVL00YyXt3Ockz1Wq9Y9ZP3pLruskJNQH4bK2cG4/nCLdps4X48GHigGpE3gIXvBokfCrXaQJpx5GGJOvKIFoNe4SgrLvl6uHyQihxBKwN/LCS/VTYIWR94F4k0VVYrm7RPs1VsAUnj5eW80OTASYjoGKYWJylCpzj3vWdYPxCdFy2nRCmlvEbypnMygQ144yQ4RTtF/52i1w44uTbBBie2hcf/YB47LH/GDpd/SHXfMWVfqfB6ch8jvYBUG7R0CCboMPDn4/5PpfBl2P0K2jvz0S6zZmcFW2GS1SnjRWB5lTkE7z2UA0jbPhSimwu5wBQNYUjlXid0a8KqgIPnFmWWQ7hLXAebOdM4ZdSyOTYxtm2LWKvwbh/0bkr8O5p1rysoePNRkCo8FrK3JOUaW7cVOFc24KZlM2q63HUpZY62asywnCkEQNRtC5qhm0ktbpucm24TDk/RJBhAVOoH2XyY9qIMogKQUIUqCiuvgtXT3HQ2Ic7TK4gzAw2LKzjkR0d/XAMg69H9uc72ls1GyanSybVzWy2eGoRN6+jyxF/M8O420Z/dpSRIMZ+gs5TkrRtealgWx9yB1IxjiplWPm5YtsttiQwmxOTuKuI/ED3ZPgXA7izT25mPQ5qPVki6M9v6mssEPBBOdQMtWej+Ju/dvwHLTA2wtGWhKyowPAWQtMvMwKbNXE6YQ0zCLXOOXZ6Wwzy7rKAIpcaM7TDIopp0HQkxlNnum+hd4kWp3PYoh85L6sNORR+6zfShu/kB8KT5o6ZFseMwgjGzHVunVhBqMocSx7EZN4lt25p+pkE4BUdAKeUONe15mDfxxbeN+ZMK5qIZ5uIuYU4Nk1ObM4sTTFwAXrs803BdTB3uuCYD6LXDa1MCGgIxAOeuYzumie885juzMD9shvnhbMz5xmEOQbdNGFhpAibe4WDkHQW6bTCbcptZ1HWYa2HtZ9sEwiLbdQBt6prYcYud0oVWe7dQ7zVDvXeXmL5O1G+d6+J0mMBMZKCUi/WdOM0gCoUL263PP47i7PFBlgj/SKDd1+gkSLpIwBTEuQj8fiQy9PnfCX784BgG2DfQcZz0RE90RPRQ36ueV1aGDB7QKj9tY8O6NPOSTCUeSKqCZRDiTvxz8jAbT2w9wT9zMs6enc114jgUXjReZ1/JAR4/EhVQV9lIXnz9bw4PU4AUVsqpjltdcy5JvKECQ7Ud+P0kyDJEvrgqjwvPenE0K5FAHq2zMN8EMJ5/RHS3znuiO/rqD7bdGlyV9+mHFlIbD3e9hqheP4MqPsRkk3n4JESkiYrO1q5KhvV+Exe7eWnW7ZvkuTD69wvGRfcxuVW/kbnZznUukoN7heOMfKhdmxDd5Xyo3n29LvY9lFfaneW+qO7mv6e646BwX54+MWzswOitKRGmpVqIG/BgUmobuNqlOTPD9LXrz3DWdYRzG5bvFn3YOoBsz9gArN3/a9+tDcD5SHr3DMl7HFXWJvq0lOj3QpnUp35fREdh0BPowTsRhO2HTxMRqB0AleufiKQrItQTh6NI/iGrpQZechSIJFs86aerJv01KrGupB+7pX+5Tth0uTQ/2Kg0X29hgDFqnOfTK/J8VWpZHybtzsry//xufhSk6gHHMoHeU6LEBndtiDcJdSxsE8sqSLlYyUa9pn2oyr2oBNWSV6ZoLHu2oLaxOeaCTZkLL/EvD2qtojEM45O34jAUp0rWFW0SA5iSrN19Oy59nerTDL3xQY9Cr3rm++f3jdD7fjn0mpmJhuDxBcGrlOxuPHg7JerVgPdDI/B+mAYP7KBNHfCGrkMc22brQK7IXAufX6q9MO8tdLul5LIGuh8bQffjNHSmQYEFLiEYoh/imNZf2C2IXX1UxUpRVTcQ6CiOeiBACOci9ASGT0+C6EiECwRU6nTlYHSA0jgM5e3d8hCpl52jIxFF+Y1edCLkKA3OX9iqoVgN2msLxaxxWd3M6KsWE17C5ClgcjAaDASIM0VJnHpKeL3k4g8pyH9r0aKOCNCuBkkkvaCToQDuSeQJGPR6K/x+Nu6NHsiXdF4kF58uvhXIxQ8fq/u8kd9HAEkEA8kXkPx+3IF75EHa4gjxVRGKbwohalA6eRRG9JYGN1xnsWi5XKD37LbfJriuCj2Qi5YEnZLEaiWgz++dfLhhrlKl+DbOvGzafz7T/rP94M/vH2of+rziQ5997g3j9PF8RzqlnPkty0GwjiJkUC5qutRyCMMEW9QqNhSJxU3uWJZNueVQtoqE6wKUQhJKzM+1iJ9Vw5SfGoUpP12ZHjgrxyk1dnFedrD2MMW8iRCzniOTEAJTfriKKUvzZeNYwwy75LPyGEOaIjzly9ZCmzryXEq3TKFPjSj06aokDdN1UGje1uz9oFDNS0jPCgCnMTuaD1npJaSjO/USEjFM7bX1u3zK0zDOJzkzb5Prel40qoHiuYaiYqhKsIQNYAnvFCyO4TjEdoDkNhgtatJnbVKkTWbZ0hVHiw5fO051r+8cVVB50cShvFjSiYBM9Bv41NzACBhAAgNNbIvb2HQgWrv2t6bCithfNhH7y/skdlO+OZUL2qQgeLPe+a/0rnid839Rcvgvq67+50au/udpV88Nm1DmOK6DmQNRv3uVp598W/6G9hDmOflpq1Ny8gQv5uWbFri/mOXEo/lgTJ+LRzdyKr6+XZ1SSjlBDmLbZYdvGcylk+bqmvzIrb3ikMcOVT4Om2nA8N5oADFs22Km5TAXQjtqYhPiCTOv0uRl48mKV9xMd9KDNeH5hlRGmKX94sHFp15oIP2jMKk+ABdfLL6Bay73ovp69mi5wZzqHq1pYDZV5rBMdcOHjapuyGs1qDVX1euqG1ilumFeSLR3VUi05p/7ubYXydnS+7DzxPP1fdmmbmODXs9GdU3auqddz9cV1/OxQar68VpS1evk49wKWJwXUxWHIuBRiurh9aWi9Z5/pviTZp4/uTeef63w3ECE9zroDmvS35lAv2qSBb9azuSv5bdnIEQj09nqug7T9sZHBN/lRwSvKoLca344sLfYscANCpUZmLjYZTbHlukyi7PiNM12HIiEIaV2bNvm174zsDd5IPBKy3ivuj/wS6P9gV/u7mlaE4tz8wVb9SSZcZo2kypLE2bjaAO2qFwvbRa0uf4DtL3qAVrBl1kHaL82Ys2vd/cA7e6yZoo7V7qZa2HQxvEIG/LXJi7dDBm/HSa9ErYo+CTwTGylH1O8klSzqTWLYL81IthvV7ol+y+3tB6CTdHsx5k0229Cqv2NohAt/VyH69o3VNmxP5sxs3jzeyPe/L728vv/E7dUv/trVaqF92SFdV5yrQqHPwhZOpy/GpeinSe7qCOy5OK/vQwRBxt55bYsz774owNCmR7hoepxAGOnIjvPUBr4fdQPoKc3ShG9rEqmU3XJETofpR6MEOmHPPUSecdhHPayL3S1MslvSdQARI+V1ymnATQVI6C+F3ZQGkP/+OJb9MDFD43Ft7WthX8/85bLkq18JyP/3fNlNrbjDdzYZqT5z/Pwysb2o8lfxJffi/8G48v/AVBLBwgY4h4VHg0AADhjAABQSwECFAAUAAgACADTle88GOIeFR4NAAA4YwAADAAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAABAAEAOgAAAFgNAAAAAA==" framePossible = "false" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" allowRescaling = "true" />--[[Benutzer:"chris"07|"chris"07]] 17:07, 15. Jul. 2010 (UTC) |
| − | <ggb_applet width=" | + | |
| + | ==Beweisen am Beispiel== | ||
<ggb_applet width="1156" height="522" version="3.2" ggbBase64="UEsDBBQACAAIAJp47DwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s5Vvbcts4En3e+QqUtmpedsLgQvBSYycle7a2UhNvUuNspmpeUhQFSYgoUsOLLftn5iU/kDi1P+B3f9M2AFIWdaes+JLVCyUABBp9uk93g9TBy8koQmcizWQSH7aIhVtIxGHSlXH/sFXkvWde6+WLHw76IumLThqgXpKOgvywxSzaUu2FfPHD3w6yQXKOgkgPeS/F+WGrF0SZaKFsnIqgmw2EyGvtQTGRkQzSizedjyLMs9sOM8mreFzAKnlaQFs46r6WWfXzuV5wHMn8F3kmuyJFURIethwOosO39yLNZRhEhy0bmxZ62KJzndDEVO8gSeVlEudq+O3kPWhBKJOXAjTiqbaD53qjB6III9mVQaw2o+WAQQidy24+gLGEOzCnkP0BCMspNtOFSZJ2Ty+yXIzQ5A+RJrC4a1sOYdxxCae268NtF2UP9izsYua4LrWx60FPBgKDJDaA4zrY9jH1PRduhHtWdumFxdmpyHNAMkPBRNzquJ/Kbu3Hq+woiW6bxomM8+NgnBepNgNWNp3mF2o10FuqttiO+5Eo2yigNBDhsJNMTo3emJn63cVY36IF6vSPkyhJUaoQAfn75bVjrnqMknQ6CusxWI8o51CTTvuJT/UIfe2Yqx4VydiIVu6cVLsmuFpGZkg1wOTKeqebj4KOAGtooSKW+evqB1jNsNwqMTf8uxh1wG1m7WY6J9nXnAfP5yzuYCjSWETGrGLAtkiKDJ0p+zVraUG6IpQj+Gk6SpUECq7/gACmtSv6qagEN05nFKZ7a6Y713zwvBJCyZCBrGEO7AH7ydVejsS5kJmIUTBCR/BtLEWkHD4HZ1Pb7gY5jGqp6c+TdKi54Z2Y5CjoJGcr7wedKYXq9UUkRgJcNNe2pU1zquOT1pSPEk0tFYmU/bdoQfdSO9MWGUTjQQAtVqmIKLgAoplVjZ7vJOnWFRbEoHitDXD3sZpAQTsWoluSa176AxrDlNq7ZnDT6s7Q5LD1DFYGk77QIsCXS3O7HmV8URGPXpmVhmKUskE9R9+HemzL93bUTpiMRkHcRXEwgpWOZRpGQitFqpCDAqxsCAVE6cooosirjtBMVk6xoGrwBhlOVRm26kSUD8DfY5Flmi3zWV5cjcfM7lcBgneHYyvhIJyJ+AxES9IMoQkukbrAZkF0WbVMiLFb6CNl0yWZQQaQT+UEtavx7WpUG8LxMwqY+orG26ycuG1X+LZ55RFGoj9jI3Vm2BMMKJQ9Ga6H+jVsdg7oIwP0yQLQwXqgld6mEAU74lyPDZsd7w443zqOgQe0yTU8xgMb2MKc5uUI8rBQ5us1/yrOIarBpufUHxr1B3BROVq1qxkc2utxqHNbeyduc2ytY3XpmMvdtay0uyt711V3KvqqfU5x7VUE1Vmvr6ycrdJIZ7XpuvukqDvFjEXjJbg0XuCEhXxvzR7WWa9WY6RCztRaIUwtplZDIcYqp30Tv0uDOFPlkBkzk7KtiMQ11ug+/uiwr2ANCzMoTRzuccx8z3O4X/nGYvtlyU3fmpPeauqY56N5fzpuwj/HO/EPoaYQ0tfHkl/BfZz63AVgGLYpszHXkAEyxMVQa7q2h23seHfhtrdJdNFP4uXcdmyCwiLFQR0UQaFJytjxgZiBof4CqUPnA9kEmlm2gmU64bdzyPlil5MZiEkTiFezyzy3K8080I52j5sqB5y1L7+0OuLOWiMzNEGh3fNsBqNd7lGOnT2xxj3Egnm0wieI1nKwbMujLqBk+44DmDluCZYq2YjDfAyd3CPuEwar8wTBmib+0+Rpfe704BDUY4U+a2wYKW4+bwoF+khsiocer+YAmYpSj8TiLnZ9h1HH9W3Pd7yNldzapIzgxbSMb4lpk1Q3SMPbOOxUjVGUnP8mepGYaH3WlQ8Yj0AidaL92/R4dw7DpoXK8aoCWzQrVMTTKlSWMyNUK/U4ZmO7qsGhxfcZZtyhxHEwbwD1A3vmcuDLI7T2AvC9ZsD3nhbwS45XsD/3+U6gXeTbfjNo+4+/Al4Elt+ePOzr3OyBoufUQ3X0PF4SPZvFzvnIiS3X8bAPIZP4NqbUoZuwXF4fV+nQ7nGzCVAN4uYMNHcJnJszm8XoeXNFG4FzRTeiQx4KnSZHPY8DnZNNeedVs7TzaiHrxJaHqeO7zLE9bjtuVdnu9tyOcPZN0OGPEp3jKjyt8p0vjcD5shGbHXnt+8Nm3dnoL4tnow2qpkf05Jkwi9t45kPKstoitWbVvq+H9v/6bpRHLGobfTHLozV9sbscJS95tlvG0PADWaCAwXoGqD2nGezl6e59palNjuT0idzs8am7p4R2l0fwwRKYZAOY5JOCqdE5N+Dkzp6cet8ApnXs889N7PNE3hlyLE+9HOkzm7qU4fKJFkDBuU0YsTlnvo8d9V5lI+KejFPQvZKv1Id6mQ1EhI7D1o9/Fkn+s3mlrSfjbhH3f/w7wT+/ipF6c/U0HBSAzjCIYwRGDm0xOg3yS/iSoXeDIIKLHj+Sub7hROQDpaBlL8mhTtlomVW1pHVkcxCtVZfzIevrLA/SXD+JRdotPIsz7hLXB0O39UuxCjaAzPcppFrgMzarxYmdUsMTkxounk3dfG1WVn1dKKuI5WAwIxvc2MVgaTtWVfXcUF/vr67i22WHzVR/VFP9ktOGr81qpq/LTuoZFLOuT5kHnMoh0fi/0P1y/qE1/iEWkEQqwkEsYDMw3e8yHoqon17/9/ovxReKYqiFfg8y1Lv+FEVANjJFQdH7CZ0L4KZuUd6CoFpFBUB9c0VR0O1KkWb5S30/s9B7+BUOpOgI9LaIhzk6NlPbM+ufS6GIbKUYHMSQAvXT5PovJDNDe9PF0UeRX5YLOhb6o0jRr0mcp0lU0qi6odDSg2xzC6AgvtRvM4KmMuDJn/Q0CD7AzGKkbwQN/Hr9KcvDgRo/zOWZ3mIDSqV3fsV2f4zKoVhlnHmcEkgsIIcoKRUznwJLOYS5TB1Jr6DU5bbFStu6+YL+gYxeSu2gLdTDtlZPmMRdaQI/jH5TDh7el+5UscIdj3nY9TxGXVI9xHE4d1Q27fk+J2690FudVHWSJBLB7Wsnw3kCmwm192M8b3q9TOQ6NeLmbWpG1yewwVjDodtqroWqU5W9Pr+9anaMtodnt2tDwpJHt9u+u7PzETTb6tHtZp+1K5+92sVn7Tv67Mf79FmPEI8RxyE2JPW0Op2xme3YqggG4sPMtXdz2o+Pymld47Sc7uq0V9sZD6+M5/MuxsPvaDzRQxE+rv5iAlU5oZ5LfM5VEOW72U70qGzHZALUc3a1nc/b2Y5TS0Rdk9xF15+KnsnsTCFr/lYavdw+y3IeV5blgjcyF6yGOn6ZZT2j6mQBMi/MfYo9312ZKDyf/Rud/rNp+W/bF/8DUEsHCMh3h2XnCQAAnzsAAFBLAQIUABQACAAIAJp47DzId4dl5wkAAJ87AAAMAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYS54bWxQSwUGAAAAAAEAAQA6AAAAIQoAAAAA" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" allowRescaling = "true" /> | <ggb_applet width="1156" height="522" version="3.2" ggbBase64="UEsDBBQACAAIAJp47DwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s5Vvbcts4En3e+QqUtmpedsLgQvBSYycle7a2UhNvUuNspmpeUhQFSYgoUsOLLftn5iU/kDi1P+B3f9M2AFIWdaes+JLVCyUABBp9uk93g9TBy8koQmcizWQSH7aIhVtIxGHSlXH/sFXkvWde6+WLHw76IumLThqgXpKOgvywxSzaUu2FfPHD3w6yQXKOgkgPeS/F+WGrF0SZaKFsnIqgmw2EyGvtQTGRkQzSizedjyLMs9sOM8mreFzAKnlaQFs46r6WWfXzuV5wHMn8F3kmuyJFURIethwOosO39yLNZRhEhy0bmxZ62KJzndDEVO8gSeVlEudq+O3kPWhBKJOXAjTiqbaD53qjB6III9mVQaw2o+WAQQidy24+gLGEOzCnkP0BCMspNtOFSZJ2Ty+yXIzQ5A+RJrC4a1sOYdxxCae268NtF2UP9izsYua4LrWx60FPBgKDJDaA4zrY9jH1PRduhHtWdumFxdmpyHNAMkPBRNzquJ/Kbu3Hq+woiW6bxomM8+NgnBepNgNWNp3mF2o10FuqttiO+5Eo2yigNBDhsJNMTo3emJn63cVY36IF6vSPkyhJUaoQAfn75bVjrnqMknQ6CusxWI8o51CTTvuJT/UIfe2Yqx4VydiIVu6cVLsmuFpGZkg1wOTKeqebj4KOAGtooSKW+evqB1jNsNwqMTf8uxh1wG1m7WY6J9nXnAfP5yzuYCjSWETGrGLAtkiKDJ0p+zVraUG6IpQj+Gk6SpUECq7/gACmtSv6qagEN05nFKZ7a6Y713zwvBJCyZCBrGEO7AH7ydVejsS5kJmIUTBCR/BtLEWkHD4HZ1Pb7gY5jGqp6c+TdKi54Z2Y5CjoJGcr7wedKYXq9UUkRgJcNNe2pU1zquOT1pSPEk0tFYmU/bdoQfdSO9MWGUTjQQAtVqmIKLgAoplVjZ7vJOnWFRbEoHitDXD3sZpAQTsWoluSa176AxrDlNq7ZnDT6s7Q5LD1DFYGk77QIsCXS3O7HmV8URGPXpmVhmKUskE9R9+HemzL93bUTpiMRkHcRXEwgpWOZRpGQitFqpCDAqxsCAVE6cooosirjtBMVk6xoGrwBhlOVRm26kSUD8DfY5Flmi3zWV5cjcfM7lcBgneHYyvhIJyJ+AxES9IMoQkukbrAZkF0WbVMiLFb6CNl0yWZQQaQT+UEtavx7WpUG8LxMwqY+orG26ycuG1X+LZ55RFGoj9jI3Vm2BMMKJQ9Ga6H+jVsdg7oIwP0yQLQwXqgld6mEAU74lyPDZsd7w443zqOgQe0yTU8xgMb2MKc5uUI8rBQ5us1/yrOIarBpufUHxr1B3BROVq1qxkc2utxqHNbeyduc2ytY3XpmMvdtay0uyt711V3KvqqfU5x7VUE1Vmvr6ycrdJIZ7XpuvukqDvFjEXjJbg0XuCEhXxvzR7WWa9WY6RCztRaIUwtplZDIcYqp30Tv0uDOFPlkBkzk7KtiMQ11ug+/uiwr2ANCzMoTRzuccx8z3O4X/nGYvtlyU3fmpPeauqY56N5fzpuwj/HO/EPoaYQ0tfHkl/BfZz63AVgGLYpszHXkAEyxMVQa7q2h23seHfhtrdJdNFP4uXcdmyCwiLFQR0UQaFJytjxgZiBof4CqUPnA9kEmlm2gmU64bdzyPlil5MZiEkTiFezyzy3K8080I52j5sqB5y1L7+0OuLOWiMzNEGh3fNsBqNd7lGOnT2xxj3Egnm0wieI1nKwbMujLqBk+44DmDluCZYq2YjDfAyd3CPuEwar8wTBmib+0+Rpfe704BDUY4U+a2wYKW4+bwoF+khsiocer+YAmYpSj8TiLnZ9h1HH9W3Pd7yNldzapIzgxbSMb4lpk1Q3SMPbOOxUjVGUnP8mepGYaH3WlQ8Yj0AidaL92/R4dw7DpoXK8aoCWzQrVMTTKlSWMyNUK/U4ZmO7qsGhxfcZZtyhxHEwbwD1A3vmcuDLI7T2AvC9ZsD3nhbwS45XsD/3+U6gXeTbfjNo+4+/Al4Elt+ePOzr3OyBoufUQ3X0PF4SPZvFzvnIiS3X8bAPIZP4NqbUoZuwXF4fV+nQ7nGzCVAN4uYMNHcJnJszm8XoeXNFG4FzRTeiQx4KnSZHPY8DnZNNeedVs7TzaiHrxJaHqeO7zLE9bjtuVdnu9tyOcPZN0OGPEp3jKjyt8p0vjcD5shGbHXnt+8Nm3dnoL4tnow2qpkf05Jkwi9t45kPKstoitWbVvq+H9v/6bpRHLGobfTHLozV9sbscJS95tlvG0PADWaCAwXoGqD2nGezl6e59palNjuT0idzs8am7p4R2l0fwwRKYZAOY5JOCqdE5N+Dkzp6cet8ApnXs889N7PNE3hlyLE+9HOkzm7qU4fKJFkDBuU0YsTlnvo8d9V5lI+KejFPQvZKv1Id6mQ1EhI7D1o9/Fkn+s3mlrSfjbhH3f/w7wT+/ipF6c/U0HBSAzjCIYwRGDm0xOg3yS/iSoXeDIIKLHj+Sub7hROQDpaBlL8mhTtlomVW1pHVkcxCtVZfzIevrLA/SXD+JRdotPIsz7hLXB0O39UuxCjaAzPcppFrgMzarxYmdUsMTkxounk3dfG1WVn1dKKuI5WAwIxvc2MVgaTtWVfXcUF/vr67i22WHzVR/VFP9ktOGr81qpq/LTuoZFLOuT5kHnMoh0fi/0P1y/qE1/iEWkEQqwkEsYDMw3e8yHoqon17/9/ovxReKYqiFfg8y1Lv+FEVANjJFQdH7CZ0L4KZuUd6CoFpFBUB9c0VR0O1KkWb5S30/s9B7+BUOpOgI9LaIhzk6NlPbM+ufS6GIbKUYHMSQAvXT5PovJDNDe9PF0UeRX5YLOhb6o0jRr0mcp0lU0qi6odDSg2xzC6AgvtRvM4KmMuDJn/Q0CD7AzGKkbwQN/Hr9KcvDgRo/zOWZ3mIDSqV3fsV2f4zKoVhlnHmcEkgsIIcoKRUznwJLOYS5TB1Jr6DU5bbFStu6+YL+gYxeSu2gLdTDtlZPmMRdaQI/jH5TDh7el+5UscIdj3nY9TxGXVI9xHE4d1Q27fk+J2690FudVHWSJBLB7Wsnw3kCmwm192M8b3q9TOQ6NeLmbWpG1yewwVjDodtqroWqU5W9Pr+9anaMtodnt2tDwpJHt9u+u7PzETTb6tHtZp+1K5+92sVn7Tv67Mf79FmPEI8RxyE2JPW0Op2xme3YqggG4sPMtXdz2o+Pymld47Sc7uq0V9sZD6+M5/MuxsPvaDzRQxE+rv5iAlU5oZ5LfM5VEOW72U70qGzHZALUc3a1nc/b2Y5TS0Rdk9xF15+KnsnsTCFr/lYavdw+y3IeV5blgjcyF6yGOn6ZZT2j6mQBMi/MfYo9312ZKDyf/Rud/rNp+W/bF/8DUEsHCMh3h2XnCQAAnzsAAFBLAQIUABQACAAIAJp47DzId4dl5wkAAJ87AAAMAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYS54bWxQSwUGAAAAAAEAAQA6AAAAIQoAAAAA" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" allowRescaling = "true" /> | ||
| + | |||
| + | =induktive Satzfindung der allgemeinen Umkehrung= | ||
| + | |||
| + | <ggb_applet width="1209" height="575" version="3.2" ggbBase64="UEsDBBQACAAIAGRj6jwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s7Vvdctu4Fb7uPgWqzmSmM2uaIAH+JHY8sr1tM0kbJ84mM3uzQ5GQhIgCFRKMJT9PX6A3vcpd7vtMPQBI/UsW/ZNYmfWFKYIQcPB93zk4BKCjk/EwRZ9ZXvBMHLewZbcQE3GWcNE7bpWyexC0Tp7/dNRjWY918gh1s3wYyeOWazktVV7y5z/96ajoZ1coSnWV95xdHbe6UVqwFipGOYuSos+YXCiPyjFPeZRPXnc+slgWswemkRdiVEIvMi+hLB4mr3hR3x7qDkcpl+f8M09YjtIsPm55FEyHT+9ZLnkcpcctYpsS57jlLD2EIlc97Wc5v86EVNVnjXehBKGCXzNAxFFlR4d6oEesjFOe8EiowWg7oBJCVzyRfVXXDqFNxnt9MJb6rmkuzrI8uZwUkg3R+DeWZ8oeVyE9MXfEtdVdAYZBj1TfTObvdDPs8yWTEngpUDRmM8R6OU8Wbl4Up1k6KxplXMizaCTLXJPqVkWXcqI6gL5yZXBb9FJWlWHAvM/iQScbXxoUXNP0u8lIf0Ub1OmdZWmWo1yNh0KF6toxV11HWTqtZes6tq5RtaEanT7HoaNr6GvHXHWtlAtjWjVyXI8a23U3vECqQMEIWpwOPo06DLhtoVJw+aq+AQ0MZkNVX/hXOeyAE8yrYNomvq82jw6X9HM0YLlgqRGJAG7LrCzQZ6VG05c2JGExH8KteVBBEim6fgUDTGnCejmrDTcuZADTT+15IS4VHx3WRigbCrA1lhALYDxSjeXX4YD181L0MHrXB0UWyncl+M1x693H6OTkpIWSSEJFFQ1YyoYMfEdqmWiVTeFq/45b01CRaa9fRnRuzGBKwrUdqv7rqvrQPIRvr9WUVl+UjvoRlNRuk0YTCBHzMOje/pkli+BEAkA2PUo2Ug0oGkeMJVVYlJX20Qia1J60YC9AW6AxOKwVEnBfbQF8uDbf1pWM26mIoTt2K00Y0G6A780qeCY4Vs9nun0QdLp8zBJTMutpNuhQhyzTbqMhx9lwGIkEiWgIQz7jeZwyPVKuJgAU2UY4KMIKAjO+UtaPYtNc1cgKgiAiHk8RiluLoUT2wWMFKwrlU1N2Dx9Yo/btOdjJdJh8mPgMlmR5gdDYrsQ7sWty6pIxIHpgphpcFV3jOebAGXI+Ru26fruu1dbzqRU69uwPGGq7VQ9tAg0bL2hT0wepbPskjP2FiZPgXTHv8ni7KN5GkyVFvDF6UMJYVkS0XRE5tFUzGd23Hh6A8pmHGRiVjx1A6kDD+T9P+5xtuV4ToSyRwYeQUsVcTiFNVZB7ISRMYUxPCasz04CxkUoJXot3eSQKlRsuxojNrE4bXuI2NtxGK8ye1WHgYjvFi2HzbN2ssxA4NxDoEc2gunTM5e4c3jpKbhvhxa0mhvsb3g0zg2MFwVygsJ0aAT9c/LvLvHGhEVkW0rKC2k2E074VrNgxebC+NpxzX3e7BZMKM+PnjrMN9vtKV3yLejQIXJf41KWeX8UYx6LU8Rzihz5xsE8bZjI3RfD2phm9s3v87uxX/F6D6EQhSlyCsedRh3jEdaiJ5Y5jhb7rOS72PT+kfuDvT2TfyPbFCtvJ7mwn+8a25y6w7Rq/IpYXzLubo+n2rZB6gWvbAXF9n2K8P2yvT9kN4X4N4BzlvSYpe28PSH9EWTkmlk8DEhAckBDU5IXLafmaaK9y9NXYdId8fVNm1zOi6KxI4tQ8aDI7n37npGfm6di2wpBQzw6x6wPkQaAd3QVEbUDSDbEHyQAO7v+12KAWrvGxfhMf6//hY0187AD7lkMwxTTAFDwsdB+Tj/WNKJIVSZw397Hzb+tjs/T3wPHMZOnv5oLApRPY1Ce2G7gepZA0VblVQBX+EAqpTbzQo3dxwlegwSW0zzdFNLYdZyXnKYxsD/zvtmnsgWtBPkMoUZkOwWFAVhb0b5nZNOLpdJNXdBvw1N03npokoIRaNLAdDxPiwVxGyIPTtCmCdQ1XbIWrs0bLPo8mPyChRQm2qRtADAodatY/ICWAWcQOfM8JfJe49fs1teCtz4eAFYK7BI7v3SZSXbKeKl+fL5yuAMu3A1tUrdXQ8Vv6wS6LbvfvBp6FbZgcbByEtksc36myM+IEHrxpeR72IE8z6FNiKYIgbbOxC69ihO7Pa9h6zqvAd7bC+cdmnH/cK86JBZ7lhKHv+KHjERJW2YQVwNxEffDE0MaObbIB37Ncx/VgbrJ9eGVy9mgJfT3nZ4bz8xXOB804H+wT58tujuudkkU/p67mPLBsHyZG0EjghZjSPVpuWc95lYi2VzhPm3Ge7hPnS25ODefLXl4lothddPPgvjKcB+GcjUc5WKJW9ytQ37GxhAHCg+PWk09lJp9doBJU8QYVHC7XV4yjLiskQxelGEhmofbp2TliXKC3LO5LFg8s9OQv2H52yq5Yr6qG2pYu+5ChQSQEaqOUw0NxYqrO/v3GeNwXTLXH0OtcFoAbB2LAwPbPCCxgQ5SU8P1cdVbo70RiACgNCqkNjcouehKNsuLZ5ajMUSTMDarqWGZQGohFjUoYeWsRhu+pv0JGudT7TUgv/ziQx1XCcxc2SW7m01ng82+AYil6GuIcTY/doIQV1cmbIpLXrNgdKOe7AqUP0RUs593ZYUB9lgxQKupzUusg9S08f7TAnvq1vVTaBGt3AevzEnU4CDMxYLeFvMpysBZEzvIT9FJpkqEkKtDLr/8uJJQKpVilai3mUf71S5dBSI77f17yFP3vPQSCEr6l/W+RyksgcY5T0+Z1qc9VluB9ORNPTeHuRLuPzSM0Y8RaXPXcvKHdybKURWJq71CPB/oo2UocvcsJqN0HOVuMgjdlsxvrbd2OjaOR3ozVZRdaHgKps6kghWEpgf3ddEoWdPqBCdPKBy4GLEUX7TdaUjrKQvEFuNcIJMvZla6ghaPqXzIVrS/eIFD5zyBkaMaCv90lRXaX1PpjUOIb6s1ee8KANosQdAF5FR0AvvMyj/tDqAyWKad9mTNewDVR5Wrqq2bhBsjSuyKbfVNkTSJtWyHZMfxu9ezsUXm2mVmIG+zs2a++/rdY48u75OgXm448jJrl6KMHzNEd26yA6Wunut49U1972mei39rwfKFvcnXb8vFS7b3L1b3FfAMA0z+cALtU/s0LyIw4RBSBLmUJF8nENHabxPgXLrpfv5i8ASJ+Atn231k2ZBKCfZU6f/3SYXkaQXASJo1/+tfdw5B31zD06VuGIa8+lWRvzrG3Bp5PjyrwVAlS6O0ceD4wrib8HutLw37xdHsQ0j/n2HBuFi7OuuM4//vP9lCkf3MwBQdqL2GKLeqDp6uNBz8kQejh3QFumEVgexV/vKPMmuxBRXk8t+5eF6ZpdvWWdVM21jBvCQ5bRSkelSjN2VTXc3cW5T942r1hveoiSye9TGzai9BCVCuW7roVy/ccmo0H1bnfSB8Ahvod/QG+EesP5LiVmJPg23aHjBk1htOWH24u1YuNQIlal7qlUG+IccuZQfT7dxrPH9szN3n+MlWd/aPqx91V2U5VvHdU/cCbIdupSvaOqh94D+Nw/tek+hfU1U/In/8fUEsHCJ7ZrSJuCgAAdD4AAFBLAQIUABQACAAIAGRj6jye2a0ibgoAAHQ+AAAMAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYS54bWxQSwUGAAAAAAEAAQA6AAAAqAoAAAAA" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" allowRescaling = "true" /> | ||
| + | |||
| + | Nimmt man statt eines Rechtecks ein Parallelogramm, so lässt sich die Umkehrung des Periphriewinkelsatzes finden:<br /> | ||
| + | Die Scheitel kongruente Winkel, deren Schenkel die Eckpunkte einer Strecke AB enthalten, liegen auf einem Kreis, der AB als Sehne hat.--[[Benutzer:Tja???|Tja???]] 09:39, 23. Jul. 2010 (UTC) | ||
| + | |||
| + | =Beweisführung= | ||
| + | |||
| + | ==Satz des Thales== | ||
| + | ===Satz des Thales=== | ||
| + | Es sei k ein Kreis mit einem Durchmesser <math> \overline {AB} </math>. Jeder Peripheriewinkel von k über <math> \overline {AB} </math> ist ein rechter Winkel.--[[Benutzer:Löwenzahn|Löwenzahn]] 15:07, 23. Jul. 2010 (UTC) | ||
| + | |||
| + | Ein Versuch den Satz des Thales mit dem EP zu beweisen: | ||
| + | |||
| + | <ggb_applet width="1280" height="648" version="3.2" ggbBase64="UEsDBBQACAAIAOhL+DwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3VrNcts2ED43T8HhuaIJgADJGSkZWc4hM3GTqdMc2umBIiEJNUWqJGRLfqvm9y3yTF0ApP4jh5LcxokPNBfL5eL79g+M289m49S64UUp8qxjI8e1LZ7FeSKyYceeykErsJ89fdIe8nzI+0VkDfJiHMmOTRxsK/lUPH3yU7sc5bdWlGqVt4LfdmxZTLltlZOCR0k54lwa8SBKS5BH05lIRVTMX/X/4rEslwvGxotsMpW1kXicvBRlfXum3zdJhbwQNyLhhZXmccdmFDyH397yQoo4Sju25xoJ7th4YxFERK2O8kLc5ZlU6kvjA5BYVinuOACClax9pvfZ5tM4FYmIMrUZ7QcoWdatSOQIdF3sgU0uhiNwlnnMmIvzvEiu5qXkY2v2Oy9y8Mf3HewvfxA8NzdLBGHHoys/sFSCy+CLR9dXfHjoq0v61fzmiksJVJZWNONLlIeFSNZuXpTneboUTXKRyV40kdNCxwGpRFdyrt4GyBVqk91smPJKhoGnEY+v+/nsyiBHjOk384l+RDvUH/byNC+sQnFCQaG69s1V6yhPF1qu1nG1RmVDGV2soxBrDX3tm6vWSkVmXKt2jupdI7d+jSgtJQDjKnwXm0+jPod4sK1pJuTL+gbi5rraKjIP/DId9yFvViNnYROdymb7bCPm2te8yHhqAisDbqf5tLRuVASbd2lHEh6LMdyahQqSSNH1GzhgpAkfFrx23KSdAUyvuqvBuyFun9VOKB9K8DWWUD5gP1Lt5SqSd1bCS+vNCIKzVNkuIdPUjpNIgoIqHDzlYw55JnV46OhawHRpL2pKrutDXQmq9SXgsLwzVHRQRelkFIHEqfaSRnOoFqu70/Yu82R9z1EG2OkNQc5OlAHFzoTzpCqQsgppawImdYKsQK8RK60ZJKXD3LV/4NO8Y7dch0JS3xlj+hmTXKqWaD9IxbyB6B6wzn8MsBAoe6tgoRosL2gGVpyPx1GWWFk0hhf3RBGnXGMkVFOxIlcFmBUhCFQ+VM/8cfmzdf5nhdFU1kqxMVyZ22IBIl/EC5Rje73oyBHkdsbLUldGuVoDj6HKPZyob/INehfPbsCzvCgta+ZWHM5d80LrrpbMkOZGraFKdIdWSIKYKMTM6tb63VqrC723heFJTBnckcpw1wPxroTpUqUBCWP8+zszeyhN2YRAi8VAxPtj4CVsfXcEnG+xHu1nXaG44Cv67klf5pcia2c5Yo5nqhFxfErY2nqDwNkgRoxhQouF3E/Mi0xCtwNMNtiJDTsRXNT0Vu96habufprWS2T3oBLJPM2BuvTN5QQsICfw6sLGjqlrr/UON2HbhKnXBKbeQTAhbOY4ff1euglzAhIGLszWlPmeGzKNOQzJYYAp8hFxPcwC5fHhDFTdY4OD3tcKS38/FWVlrQa7/4hqC3VCfxVXotH2HAxdPITjjUcwDV0DdosRJwxIAIrYJcjzgxNVGQ12qmJiUVUgjrZH42vOJ+pM8ip7U0RZqc6zRmdl5G7EeNcw3ttiPGnGePKIGG8xx11PJU154DB/Ne1qyh0X4dBFFDEaeq4fPh7Kd4wOvbo5bfLNG4wO/DGRfe/o0CKeE0JWUxywQH2zIA8+OuhvD7uHuq4ZG7YT8ss/+xnSB+QFuqCtngdMpjUyMJ8SRAIIYswQYQgdxlD96WObI7SXo1eDQcmlPi1VQwTdySBqgH5UxMuO59WfYNI0v/2VD1I+0zh/a7bsImXREDUpl9ukvGtEyrttUkLmM+r70GQIoaQ+KhyTNoiSA0hpUTNmtLzTssLc07OyaFqale1p5cv7Rqy832QFOdSHQs8Iho7gBSELjmEFuYenSgv5mhV0WlLokamya37nWzRcNJnfL36c+R0Rx0MEAgdmRwpR5NYDPKUhhUECuwyE/lHz+7cx8LwJA89/HAag6WMGaUsIwz7yFeL1GYpgF0EDBB48FITHULCrMp2vVaaL7cr0oVFl+vCw/eKYyoSrT5zktJXpIdrF8zVSutukfGxEyseHmqxO0C48E+fs+yJl78eG7aFq0OzoOXhEpxE4TJLNjzgqi7CDyY6zJw6cMKAeRYSiAIKMnuqr5n9w+Lx/cNsxTn9qlImf7s1E8n+dcVrUMEtOfMh5iPp4ed84/bkRK5/vbVrs+GzErnfQOG3qIw5Py4rfeJ4+W/2/Z/03GtXfqDz9F1BLBwjB02r+ZAYAANUiAABQSwECFAAUAAgACADoS/g8wdNq/mQGAADVIgAADAAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAABAAEAOgAAAJ4GAAAAAA==" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" allowRescaling = "true" /> | ||
| + | |||
| + | Vor: Dreieck ABC, A,B und C element von k, Kreis K<br /> | ||
| + | Beh: y= 90<br /> | ||
| + | |||
| + | 1) Konstruieren eine Parallele zu AB durch C (Nach dem EP)<br /> | ||
| + | 2)Der Winkel < ACE ist Kongruent zu alpha (Wechselwinkelsatz)<br /> | ||
| + | 3)Delta ist kongruent zu Betha (Wechselwinkelsatz)<br /> | ||
| + | 4)Winkel < ACM ist Kongruent zu alpha (Basiswinkelsatz)<br /> | ||
| + | 5) Winkel < MCB ist kongruent zu Betha (Basiswinkelsatz)<br /> | ||
| + | 6) <ACE+<ACM+<MCB+<BCD= 180<br /> | ||
| + | 7)alpha+alpha+betha+Betha= 180 (einsetzten der Kongruenzen)<br /> | ||
| + | 8) 2*(alpha+betha)= 180 (rechenen in R)<br /> | ||
| + | 9) alpha+betha=90 (rechenen in R)<br /> | ||
| + | 10) Y=90<br /> | ||
| + | q.e.d<br /> | ||
| + | |||
| + | ==Umkehrung 1: Satz des Thales== | ||
| + | ===Umkehrung Satz des Thales=== | ||
| + | Ist <math> \overline {ABC} </math> ein Dreieck mit einem rechten WInkel bei <math> C </math>, so liegt der Punkt <math> C </math> auf dem Thaleskreis, wobei <math> \overline {AB} </math> einen Durchmesser des Kreises <math> k </math>bildet.--[[Benutzer:Löwenzahn|Löwenzahn]] 15:07, 23. Jul. 2010 (UTC)<br /> | ||
| + | Anmerkung--[[Benutzer:TimoRR|TimoRR]] 16:13, 26. Jul. 2010 (UTC): Du meinst <math>\overline{AB}</math> ist Durchmesser des Kreises <math>k</math>. !?? Jupp, Danke!--[[Benutzer:Löwenzahn|Löwenzahn]] 16:25, 26. Jul. 2010 (UTC) | ||
| + | |||
| + | ==Umkehrung 2: Satz des Thales== | ||
| + | ===Umkehrung Satz des Thales=== | ||
| + | |||
| + | <br />Ist ein Peripheriewinkel <math>\gamma </math> über einer Sehne <math> s </math> eines Kreises <math> k </math> ein rechter Winkel, so ist die Sehne s ein Durchmesser des Kreises <math> k </math>.--[[Benutzer:Löwenzahn|Löwenzahn]] 15:07, 23. Jul. 2010 (UTC) | ||
| + | |||
| + | <br />Ein [[Beweise_von_Studenten#Umkehrung_des_Satz_des_Thales | Versuch eines Beweises]] besser: zwei Beweis-Ideen, eine über Winkelkonstruktion, die andere via Zentri-Peripheriewinkelsatz... | ||
| + | <br />--[[Benutzer:Heinzvaneugen|Heinzvaneugen]] 10:29, 26. Jul. 2010 (UTC) | ||
| + | |||
| + | ===Kommentar zu den Umkehrungen des Thalesstzes--[[Benutzer:*m.g.*|*m.g.*]] 20:43, 23. Jul. 2010 (UTC)=== | ||
| + | Es sei <math>\ \alpha</math> ein Winkel und <math>\ k</math> ein Kreis. | ||
| + | Der Satz des Thales hat zwei Voraussetzungen: | ||
| + | |||
| + | # <math>\ \alpha</math> ist Peripheriewinkel von <math>\ k</math> | ||
| + | # über einem Durchmesser von <math> \ k</math>. | ||
| + | |||
| + | Die Behauptung des Thalessatzes: <math>\ \alpha</math> ist ein rechter Winkel. | ||
| + | |||
| + | Aus Gründen der Übersicht benenne ich die Voraussetzungen V1 und V2. Für die Behauptung schreibe ich B. | ||
| + | |||
| + | Satz des Thales: | ||
| + | |||
| + | Aus V1 und V2 folgt B. | ||
| + | |||
| + | Die eigentliche Umkehrung: | ||
| + | |||
| + | Aus B folgt V1 und V2. | ||
| + | |||
| + | Gemischte Umkehrung 1: | ||
| + | |||
| + | Aus B und V1 folgt V2. | ||
| + | |||
| + | Gemischte Umkehrung 2: | ||
| + | |||
| + | Aus B und V2 folgt V1. | ||
| + | |||
| + | <br /><br />Also fehlt uns noch die | ||
| + | |||
| + | ==== Eigentliche Umkehrung des Satz von Thales ==== | ||
| + | Mein Vorschlag: <br />Es sei ein Dreieck <math> \overline {ABC} </math> mit den schulüblichen Bezeichnungen. Ist <math>\ \gamma</math> ein rechter Winkel, so ist <math> \ c</math> identisch mit einem Durchmesser des Umkreises des Dreiecks. | ||
| + | <br />--[[Benutzer:Barbarossa|Barbarossa]] 08:38, 25. Jul. 2010 (UTC) | ||
Aktuelle Version vom 26. Juli 2010, 17:25 Uhr
Inhaltsverzeichnis |
Ein wenig Didaktik
Hier geben Ihnen die Didaktikspezialisten Tipps zum Satz des Thales
Satzfindung
Induktive Satzfindung
--Gubbel 12:10, 21. Jul. 2010 (UTC)
Funktionale Betrachtung
Variante 1
--"chris"07 21:47, 15. Jul. 2010 (UTC)
Variante 2
--"chris"07 21:12, 14. Jul. 2010 (UTC)
Variante 3
--"chris"07 21:12, 14. Jul. 2010 (UTC)
Beweisfindung
ikonisches/halbikonisches Beweisen
--"chris"07 17:07, 15. Jul. 2010 (UTC)
Beweisen am Beispiel
induktive Satzfindung der allgemeinen Umkehrung
Nimmt man statt eines Rechtecks ein Parallelogramm, so lässt sich die Umkehrung des Periphriewinkelsatzes finden:
Die Scheitel kongruente Winkel, deren Schenkel die Eckpunkte einer Strecke AB enthalten, liegen auf einem Kreis, der AB als Sehne hat.--Tja??? 09:39, 23. Jul. 2010 (UTC)
Beweisführung
Satz des Thales
Satz des Thales
Es sei k ein Kreis mit einem Durchmesser 
. Jeder Peripheriewinkel von k über ist ein rechter Winkel.--Löwenzahn 15:07, 23. Jul. 2010 (UTC)
Ein Versuch den Satz des Thales mit dem EP zu beweisen:
Vor: Dreieck ABC, A,B und C element von k, Kreis K
Beh: y= 90
1) Konstruieren eine Parallele zu AB durch C (Nach dem EP)
2)Der Winkel < ACE ist Kongruent zu alpha (Wechselwinkelsatz)
3)Delta ist kongruent zu Betha (Wechselwinkelsatz)
4)Winkel < ACM ist Kongruent zu alpha (Basiswinkelsatz)
5) Winkel < MCB ist kongruent zu Betha (Basiswinkelsatz)
6) <ACE+<ACM+<MCB+<BCD= 180
7)alpha+alpha+betha+Betha= 180 (einsetzten der Kongruenzen)
8) 2*(alpha+betha)= 180 (rechenen in R)
9) alpha+betha=90 (rechenen in R)
10) Y=90
q.e.d
Umkehrung 1: Satz des Thales
Umkehrung Satz des Thales
Ist 
ein Dreieck mit einem rechten WInkel bei 
, so liegt der Punkt auf dem Thaleskreis, wobei einen Durchmesser des Kreises 
bildet.--Löwenzahn 15:07, 23. Jul. 2010 (UTC)
Anmerkung--TimoRR 16:13, 26. Jul. 2010 (UTC): Du meinst ist Durchmesser des Kreises . !?? Jupp, Danke!--Löwenzahn 16:25, 26. Jul. 2010 (UTC)
Umkehrung 2: Satz des Thales
Umkehrung Satz des Thales
Ist ein Peripheriewinkel 
über einer Sehne 
eines Kreises ein rechter Winkel, so ist die Sehne s ein Durchmesser des Kreises .--Löwenzahn 15:07, 23. Jul. 2010 (UTC)
Ein Versuch eines Beweises besser: zwei Beweis-Ideen, eine über Winkelkonstruktion, die andere via Zentri-Peripheriewinkelsatz...
--Heinzvaneugen 10:29, 26. Jul. 2010 (UTC)
Kommentar zu den Umkehrungen des Thalesstzes--*m.g.* 20:43, 23. Jul. 2010 (UTC)
Es sei 
ein Winkel und 
ein Kreis.
Der Satz des Thales hat zwei Voraussetzungen:
- ist Peripheriewinkel von
- über einem Durchmesser von .
Die Behauptung des Thalessatzes: ist ein rechter Winkel.
Aus Gründen der Übersicht benenne ich die Voraussetzungen V1 und V2. Für die Behauptung schreibe ich B.
Satz des Thales:
Aus V1 und V2 folgt B.
Die eigentliche Umkehrung:
Aus B folgt V1 und V2.
Gemischte Umkehrung 1:
Aus B und V1 folgt V2.
Gemischte Umkehrung 2:
Aus B und V2 folgt V1.
Also fehlt uns noch die
Eigentliche Umkehrung des Satz von Thales
Mein Vorschlag:
Es sei ein Dreieck mit den schulüblichen Bezeichnungen. Ist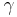 
ein rechter Winkel, so ist 
identisch mit einem Durchmesser des Umkreises des Dreiecks.
--Barbarossa 08:38, 25. Jul. 2010 (UTC)
