Auftrag der Woche 3 (WS 11/12): Unterschied zwischen den Versionen
RicRic (Diskussion | Beiträge) |
RicRic (Diskussion | Beiträge) |
||
| (6 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
#Können Sie beweisen, dass das immer so funktioniert? (Es hat etwas mit den Eigenschaften von Parallelogrammen zu tun - siehe Hilfestelltung)<br /><br /> | #Können Sie beweisen, dass das immer so funktioniert? (Es hat etwas mit den Eigenschaften von Parallelogrammen zu tun - siehe Hilfestelltung)<br /><br /> | ||
##Ich bin nicht ganz sicher, aber es fehlen hier doch einfach ein paar Angaben zur Aufgabe, oder?? --[[Benutzer:LouStick|LouStick]] 13:30, 1. Nov. 2011 (CET) | ##Ich bin nicht ganz sicher, aber es fehlen hier doch einfach ein paar Angaben zur Aufgabe, oder?? --[[Benutzer:LouStick|LouStick]] 13:30, 1. Nov. 2011 (CET) | ||
| + | ## Ja, ich verstehe auch nicht, was man an dieser Stelle machen soll ^^wenn das vielleicht nochmal jemand erläutern könnte... --[[Benutzer:Miriam|Miriam]] 17:18, 1. Nov. 2011 (CET) | ||
| + | ##*Also ich nenne den Punkt am Stein A und den an der Eiche C. Es zeigt sich die Winkel an A und C jeweils 90° sind. Die Strecken A,Q und A,F sind konguent, die Strecken C,F und C,P ebenfalls. Wenn nun also der Punkt F für Feuerstelle nicht mehr auf den Insel vorhanden ist, setzt man zunächst einen willkürlichen Punkt F`.Diesen Punkt F` verbindet man mit dem A dem Stein und C der Eiche. Hier zeichnet man jeweils im gleichen Winkel 90° eine gleichlange (konguente) Strecke ein und erhält an den Endpunkten der Strecken somit die Punkte (einen davon habe ich F`` genannt) welche man mit den Punkten Q und P zu einem Parallelogramm verbindet. Nun misst man den Winkel (auf meiner Zeichnung den Außenwinkel, der Innenwinkel ist natürlich auch möglich) an F`` im Parallelogramm sowie die Strecke F``,Q und überträgt diese (Winkel und Strecke) auf F`, am Zielpunkt findet man F. Somit es es möglich die Position von F zu bestimmen obwohl F nicht mehr da ist und somit kann auch der Schatz noch gefunden werden. | ||
| + | |||
<ggb_applet width="1071" height="660" version="3.2" ggbBase64="UEsDBBQACAAIAJpuMj4AAAAAAAAAAAAAAAArAAAANWY5ZGY0NjY3MDNlMGZhN2VlYzhkZDIwZWE3NWI4MmRcU3RlaW4yLnBuZ+2ZeTSba9/vo1Vq79JufTqoIVVCi1Ix1RRtqYQYSg1VY4tojBUzCe2u0gEhKma2mmMWc4hudmtqUJQmpqoxCCrm8dz2ec5Z66znfdd637Oev84691/3+q37vq/ruq/f9f19vtf1+p4RnPeXS7+AQCBePYSOKQh0DAwCceSd5AIiI09nfoJA4jV6OrfNAhms0c14J/NtracHGkVVOe3Ie5wcPPr3dN5/JySUywbdxsReVX2N6BYQlzTpeHXl2Jvg5vHNQrX7iV2spWFNzd1kK7sykjU5Pjg4OKxuOajbJ4NschxULuIxBQGBwk+Dbm2BQGdgINDE8b9v/8PIs+2X+MP95bC3DQe744eyO/KDbV83NdgVOz+D9kUm7frX9x9+zeQGSStjZdaHypZT18MO2JnnBFJQPDqg8j/NYEQ2Lcis2vFaq+Ex2mORWtvo5LX6pWY4Dgw6Cfbhu8Q++Rv7lyuTdz48zmwtxv8K6pLFRv0quo5So0V7FRKRuubQ82QslDTraJrwKOVM5btHTgi5X0HFBSvya59uLn+QX/spcf3+5539eBgMXe8ify72IzWPxzETt2HFXg47tN4COQRF4HnXU+CgJMunDzpde3Muc4Ja2oQC/vrMOFxh5md2T/sluRxfqIP88dHsLui79DnYjLd2aVhTz04gq21rj92T6pIRlEcPWW5K7ZJrbtxmZx42rjysSkTmWW0kDy30b/rM/gwDPhm5IooFXcbKbK5UfKMLrEtgWdVDykUWJVJDKtSf0ahdVq2XkTqrqvKUgifT8Vpo84ZBLHXcx876LcdRm+d3LYM3P2k4nbS0VxIdC5yMRuWn+7vWjGC6ZpYoy54xWgdbqIWSWk9lulP8TM2wp+BucNTwPhSP+kJtA69TDARjQQ5WkfjDLvLDK9Y6hztDzcpg3JoJe5HcI6vR4//qYu7yzMgB1UxTGfg4KlLY/+py81ofksYjmdaL3aSMe/CpTsXO2AMvtkwa3H9uRUq/nt3SVqXFDaJiEvCirZU/utWX3S3K7Eb3ttq0PPm09lZmgHQI9ZkvzFdebtocu3P1VcBYUH79/sZw6q9yjeX1c+/fplh71uduf39xWjciFlF+c7G8tdO0Sy7051sgo4AeelLZ6cuKkum+pslv5ZmfE70TXlnBqT1q405z5+1BDywmHHFmahGfsxDnfoSM79rxCMGFvHUKTfcONpvlzN8ouQ3KcL4If6m58S17u8M4tA+7YD3uqjyOZc+kju+hyMvUXWWvpnWLekYWCXYQCQ79ttjI7p5eKKMsNaxWcIsE/rG9Uds8uvedW+vJEjCAl8uCfZFf0otTwmrHwZVRUMM6gQtPdfcpBzDQSsKvYO0ZbM6luKdP+w1VlLya9zfuPLm58c0xlVUzXBp0sD3btcukfwPiKale1Pr6H2+kU/qNtZo448IJeK2DOhtW88ZCM3t/2J1syCOL11hF0H9WDtmFJGTgHWNUUVkTVcrPY0KadmBa6NdOxOmkLIqX7n6a/zQ3iGi49YCPN29zxMe48HGxdW3p9qzW4fbLWeJ07KJBB8HA6fXUzkKZl13gxMuZ0YDx613XmaeD9teHUneXm5ttTsO2HAqd9ibBhw8Ci629mqrX/G0wHRDaWznqN3cKq2a6InQtG5xw2fS4Tgs8p291JtWL2DPdsFBKOU/0X23kx6xqVJrXNp0LJPajXTQTAp6sc4LC8YP2kzwnC21yGrzHgmZxWUyF21PPjvNdVVAVCVmsWP0Z/rIZ0Av7LWG7EFZ1nzRhuSeBhJAS0tql9+gbI37XGTtYidSS2RelrxOmiTJMpzYkKmxKddqj8fBgl9YDqEflqXeueqUyQzk/CMvR5B4YJfy95uYIWfXnX2dT8zNDGzaVhBuioFXP/RB3c3eFQA70l/hgcqbfs6HHLXD/GiDjYTRUqsege8XH85AzTjwSXeJwkSAn8rAnRUmueQ+zzeCMx5ZuWOjUtOeNi9nH6yNK4WBclZmKSNjez5m6yRg32brvv/M/5hepLI6/wW8V2iGbyJkJ/LK68PTsGDVSY+YyzdSAqjyU7JJh5d+5t5avdZ1W7jZUahuYxlmwli/k23t7ehvFU0DNYwc2SXh0CPd9/hUkaDDtyKg/O9p8IPb8cpfs0UpLLalhkGyszuudRnjOhe0Oj59vge8oMPKrUUyxhDiZON/ciqqNSKHA78+nf/Lr8ksxokt5VJmQju4UGdpUyBUO8YQ4G8piJTIohp6SaqtgrPFTZzulweAsj5zKWKBjUJr/H4LV+wFP7NsLlgX6GqWwoPIrrW2mGXzWYHVNIeY24uwTokHlAuSRKBJS+HhgxXvlT+7EVCwOxnOaXkL4NCBTOKU/Dj9meEz791stSKJ/pS8GSPREV+QxA1tUh8WYmQL/Lf4bG+Nhh5XvCJv9FwjSPdOWzTvmzH3EOXGkFo6sQ/JWR6EEyDDP9m85tqqg8tvmMJRmRbXXeTjvMfSiwXH0sbt3EB7Khq/alUfCYzd4tbpkmNvf/IZsuxLm7+4oGalOv+trjosY4EwxgBoqiePHYV+V9y/x3KAsU0O2k7cP9tTNCZyZNkEwgWcbndJliol2wcwWnwLkLb8ilqLoY8ZYrDeH4wgICnrw24TjNfjr07xSp7X2nhZic1TEYNtT8TP1sxmC9dh+c60M1Fcz+b63cRlxa0QnK0nebKa8nhbiEqJfxdRrsHmf5dXFj2wxLg1PNDPpEyQ4Jwt61mV95hOoPtUXcHmszjnJ5HaJ8NOIbr6Kr+efldlMO/adXDExxy89cqP/norO96Pnjn2ONONiqBymTRJcdfPe54kq3Z4kFZVKgXscD6flwrb7oPpOaInMroTctKIyasMpDSS+PStS5KF/76n0ZfmFmuFGEb8PKWRb0JZ+BN6qCDzpWVn4ZI9pHPZw7s8C+4Bx3GbCSlxorOfcRctrcxGvwpPS7FJr4+3eipq/CH8uM10VYhwh4q/iS2EV2EqT0xqBfLTZmgtJy4osv0u82+fzhZebTk3xqAN+XI5HPg4pGEe6G3yz0qkfl2Yybi99g2UXQ51ON+lBm95FEUFQ5LRO6zVQlxpWBoVqq5rI1T+L9k90KrD0J+X0iGm39v0jBZ2TPGFS+8WooTDgxZ19VavHenUdhK5eW4nJlpacs54UDhQRUqi3bKxQfgqAjAntLQA3tpovlWV4lDLbEGHwGa8poYS0VsIjW4HcjJLq9SgimivpK94Z6f6p2CUR6TGS5n+GUUeNdpXP/2Y0XK7GKhX4n7NsTPEYr/K5YV1Tiaqz5MLZBk0nQLBOf1jCiKyK/rG6YZXRRVRHbLn9wWrir/2IyAj80sJAwAvjhDwjg/SqIue+v/r0yCYo5iYAQd8uS4PjPZ/F/26QkBrY7dvxuuq05lpve/kNV+b7ZZdcV4Jz4inu1KqpL3y6Vgd6FzsJ90rVBKp3saVNGwyopHgPrt0R/8tx7dT7+dujLH8OB6sIfJDZzRlzSLLv/Yy8971DyzcMM/+KUV96kJeDkgkpTft9OF2VIJ0lPvvJ6fuD9C55WR2dOwalMtfT/Qat7G++8hyp7CoI/cfEcSDFtpKGtmVx2m3nfc535lhdzo4I3p9Rab7W+lfliS26S+Z1S6Mew9P6pMtgQNNaHCHYqZxhKtmuodlSRN08XYiY6JbqUXMNiUz+kaLgOr+sUYh3ZLAaQOXFLW07N3ucC1s6e8mmecCoTog9+lFSO7bT55aQ981AHwdgzAU7imLlYCjBuwdSSZbkyMu4/be0AsocnOxFSNccXZH3vUfP6cgHlT9ubVO0b34nOdGNiR3tffquMJeHU7W4dH9X91PxbCxl8Y9CcJdRChtAC2T2BKU5LEeN8AbeYlia9i5VwcmU96iOUs1ep1TRAuaWT/4toYjqR7jlnOQNl3XzsyKAMs7EavNd87lN2jBs3Mfx/Fb4yuAXPqU0JzfvFLRPbqI497AzE5K/7X+olZcuD50POPaMVwIrUzudFKRZZqbF/8u8KYL3/GjGOzOo6fYWUCa3XpYxi4IHOJ54bFOFjBKPLzAOL2j7n44WZMoC8vmjpc10wzVqYThpyCfZ96ArdtavhUfy3bZYsjahiOuV2rCYYQGan6Y8HB4rWuYTsjNfkH4zPkXfhbkPenbOejtJ+eRAm1eXRtSQfVhTEABOnQmhke5KTVs/3iKX/5pOtLdDudgEjPrRzhprfDmqhi8ylmXO3tr13GO1AWVJvfPBhg192/Q4ApZI+uicaGuR4VOq0H0zWzFDJGDEm9bgt9DpQOZMWkzraPNx9bIcFw3EgZcFhbV8mXcBDL4bif/4mdU+0FftNqQMTOP4nUzt0iN8oWO6rncNu2vSmtn+AGLK2ifOa3t+F+AfLL0RVXTMtyeASTGZdcO4eh4zapoISFXU2l0kz0zFG8taZoQI99hpm90xlbpcGDVQUoPWpwUp5mcEu9IzUm8QRAg7jZhQGhgo95jqTJd9m0sP28xlGjicEEoA1zgDGVxesfSsbOQ7WdjvK8kccu+ock+fqV+82pHAzC68oQEodG5DrEf+dgZW49wLd/ioO5nW2VsGsBolbR9KunOv6Li2xHsUxd0/dcolmqSsc0nHB8KpufX9xa9a6qJif155nhMaNoJl06a9739RPaLP5djrNX4M17y8PGNxy5r1weX9uWx8Z3mlGXL+EHnH8JielLYAwqL2MEaNsyftNEj5W2dbTv2l9bymNpGQv0FVtQyiMoQOC7X2HCgUdyqal0h1N/V/M5AbqzebvWau/eNgd1luIk/2bRTFRPKqcwtTfbnx/pixg9pMkuN50tW4UXkBNSK6gMdqNiPEk84Tn5ttpl9pFn8mHpJrw3LVtcvkJChmLlF3l2iylEVTImb14OUFuwd3EKF2JKkgvskahU1z779n0jvMYyg12PND/XOUne7+r2HEbfAo5NXnj+18cad2GY/fXu/cXeeCLZ16R4UkmWn1uREuxwseVLSJWHtuFD7VAGgyVxJyLsmG51obOAzLtHzt062ab/aUUTbJDcbeu/Nx/mtRF8GU63Xu4/jpbEDNilTXerW72jfMtDC5+oTrNdtjBoa0Nv6HqzarQpWL8SS9jDalIZv7xEAor1KTxHqAyHrIJqub45nzbzBXcwcRyoMrYaNDgp5ECDTWzdTv8dxeLKJMR0rEarDdUE00X9Ml25Z5cTMwM+wgqB7Dbt5doiCdJ1+JxVzFJzvHh6eG5yvGzHRq4NdKBlqnV5exBzSVcZstYbFHRco0iQ/iryA3c65gmLmJyoBRQwXt2TC99L53+Bj2tq8OAEBrh3rme4hfVc8Di+PjrhWuyyR7a8q2cP9vw/Y5m16l+SdZ+XVeT/bwZVW87mA7NnpkyquBmYcCYP+66GXKI4bKAhrlkINWFJ0ClqlskxDd9n7toV3Y/vp08BH8xxB3cFZ8HTFEmZKcC1Pv7htd0xSRzAh8jL5kKOaW4si2YasNfBpQo2paEh0wEF+nDkjWFcpzRpkVi95OMDpmGKzlz0Dnz8TBRbbvBAqpHB4HEW2B9VHDWJxBeGl7UqvlfQZFH00eCNM9CFJ3aubyNsVUljZulXuecDK9iOZONINicKsdkvZ1zwOO36ZKiEonxJgp82v0cRO+xz0FKoqoJbVGOS8vmLAwEQn29ATsy+p+4RPx4qntzRNvGg+3JvEqgO5YFrZMzda0wgPy8SU1IPfyiWwc2+h7+63SDZ4SNoM6TP0t/83Kj7dyxHQwutfgpB6oo1KvdFEGreLIp/pbgOnLP8owfZsPY4Kbm3QAXCPtj1SKSVp7Ah7keyXb2ay8EmAjXih2zZyvLz4243Wj8Po37WCtT+lW/PS+BhQtpc+aYCtJP0EgtVpYe5iXMhS+lIismZs2iDr33WR7N8N3A0SgL33n3PphPhJIQx4bnqDCAl/7WW9zYdAD7wnHvui1I7NL1nQ9/FgsxmjDGdY05MGv8GYxyQiwbgs8JqdsQsz64TBSIr47RgBaiZ173fRW8wVqZDLvR3xusrtc96oFSQtXRl7h+MBlvn3RfLDHM/pUR+fnKOrkxIX+hS8HqjxC9ruMoc7VTgDRHsKI6XLM7QL1+1A9JR8oQ2Vi0b2DRlnCCFjuJ818p6wH9XllOHoE06IIjTPaJElQ+fvWtgJU/8i3+3FJEGzUw8G53Ya96cyOzEL/HLRC15mQpXoXgcUE2CsbVUEJUYhhBvMQ4GiV+UZa392xGZ+gbhaqT69JFOkHGi+O3IgOiVZKO1Z+paXt8UEDXjFUAjsQ/yS/voOPWfREJQi19PELHGz7O9w/aeRpK+90bJ0NM7L9IpsTHx7DGW2mbqpa4OUDwQ64tptaKA0GJOhMH3927gIsb/+tFtRdmq0co7Ha/vK2TXwNLWY+e85to1hdHaogRtbhvwEtkCYrVS4S9OHpHXHziBST+9NPtCx4wduBulUuNbq7s0PXa94yjQV2NJFNUWJAzXRvbatS+dOk6SKdK2UlTgBsNViA18z54tMnFPMwF9GszWfV5VDqrkKr6T81pr8+CVh0aR9djLOehPodBlmXQVZYZfdlVn7RFcQxVb9KdeiTwh8AKPXRAoYaLfmtrGnjYaHukS3mfIkmejdM/LFbAyzkIbF9oQs2T2/Tf8ZJIfkedg30AIYo+9RCZwKLilajXd3w/OBqaeqam62eJp0QF2QmhxKWbE4KjaXO84NkulbkkSdymhIUht3vxxXMFhuEvFhUd8xr0oZAVRVvi+0L81y0Ug76/pw7BaCekkX/Dr3Kej6NlQ+YUoO8SN2AGHgAt96uyxS7cKT4L/22uvgIoLeReP/jT2pwqGQxpIDVJQGlq+4DfETql+88nNVSJvm/5xHiMuPZZn2bcVJdt7mFB9yBBUrj4Ba6RxKth+3MZfObQVcbud6YtNbO724HsbKccP0mlg+3bswef+YsDMtDh7uPD/CfOdpdMl3fGl0OrV1Jyv6UZNyAHtTX8S+sSrQ1jW5/7qX6UfnF5/lCsuo55WEPnxj97pCOhN64LEfVlRLBiAiz465sZg6qLyg8nnoYGdRzDlBvAFl8lRHjmK6vlva2XCHOydlNFKf2R564+7CFwW/+H8UkO1HJEKQ0jwidThiLASo/KTxG6BNxNq48Tpqtu3rzaPvL2iubkqOgVxJuQFZ3QTiyNGZDo0KEX54GWehsJc1wXbJitBMHZYIG0NnZfOpucui1dduqWa8qrQzpiccsRrVzJPJTkSV9LLXfYROwmvwG87EVR3ssZregrpqZZT1uI1lPyWZv8jQPUfLWHm0vwQnAl822LppHJ/laIKT4VO3F1W0wAyG7XOMXNHRxpbIVA6wSXOay/kW9gvbLFWZqlZ8JIrFrYVP656YaFkrd/Ic9ajF7WGFtGH5FXvbVKdu85KE0fNajk/+0Kd+LBGES6Y5QkstkZZesm/+3R5GrNZqJjgNGif5biF7E5YJ94WyJIonAxr3VLppwwIjJMbg/pdiKnLdI0rOHEy0xzmPwO4j0pymz724RKhaASbu/PZbL4IAitx6MXwDJUFbkl2QSqDMfT/2jy1BTZW/NIWo4RU0qcMDHXIK2197DCFluQmajud78bW0McvLFDo2mIffNMwEBgaI0LaVE6CwMUAxUgPT08OnR3MRmdSosC67WvVghYhobMoDf47R1EWpLbmKLU+DQ9oVe7dPXZ4urvKijvyB25fnVGmaL12hfC+LhC7MLPSWlDfMkTKBtzRD1aLsQwAWbjH4AUKxhGdLabfwPTE90nIp1P1GqFYYz2LcZd6k9CQYV1wFDQI2UGOSkxFoJCsx8PcCOWzA26mW0jxlRZR+933hS5ZWmmg/xgRmpMXNmOiQzZVzqptZGwuOA2fhr9ZsjPkEaJ5KsvrrWb5w4epOeMlxSKVP9kc/L+jPUsPb9CVCXFNZX+tdJWGbrJOZ+DwZJ1GRMOA+YwxONU9gm8MLaRC+M2pL2aU2z4Jt9s3Fj+PB4gxuGcogdLVN6exaG7p8KIkgfbzfdbu8lc+auRU6FEF3pzkDOBF9ZaeSO4gGDZBZW5HWIKpjcPxUpemO4zVG5zxNP5DKrUu/u3mkrOOu2O/NsyrEQg135k3s6yCkqJDTUvz4N+P+5lwizCbYqPILrDvWf9xCXO/iS0gJTvxOkECFMlwFVObYNMRkV0Zlz+xHxyMm/xAtdSpSmpdI/PQwoWBu96nbCcQRqICxlkWoMvz465R2jNl/Arwy9rdQljZallSZqfLINGP16tI1JexQpbOHf5PTtQenXIkuVC7a+JlZ5HZszbB755A8MTfnaZbNRbDHu24jGi/a6DxVmLo2gD29+ARdinOB6pSMD9kDqyLEc0JZ8DPjA0PQ7qgDYrxZpO8gMNcQdAsh5dbZW3DenQxEpT+fw2WHmJ47K0b8SDuIVUyQKpvTvdbJpMrFYWugua0gDkCdn5Y6C10Wj47m7jYlS4U9unri1NVegrouxDWFVQ2wGUp+EdORm3Bke6vlSK3N/Flv1Qn/35/zwDpkU7GBjVIWbjFbpvFHRmCl83Y8O6dKOFMIgkg/jbG8UYjXYnxUgCMOHXK7LdUyLp8QWU88KP9J1kDQU6xSgd+mmz3REZm6MYuqgsAyLLjwqgqfeMElUxOh7lHrvg4NS76PZfoAwkZ0qhyW4aZBAYKmcwwOAWy5T4cQjMaQ6m9Z/VB0hsTkXxDXBTN6g5aZNalVJrTVHYddtHnBm6A7ayxgROpT7C5jMSTB5lCM4AsB3OP5v03TE2Al/Pk7+GYe39aEpTbNxChqfoh/0DA2Q4CXYtRPPEWfqAWOLjEV8FDNPwh62ntYaWQQUw/lC11s56oMUpE+lZwnWCT2z0npabkIssitXVYlGqmdMZHNFb+yyZntLsb5FGjjH8dlzsBncMdmjI4+4D3EsUn2fVlw2ixwVl9czsmYqelHpTVOZnPih0d2ssa22l0SSxRXTekCH8HCut7kpcboD4Vmc8YuhHX4/XksSdfvNNCxKHpq36MMy0MXVmdl2o7aqLMgfG+Vkz5PJlgrzivEm61jQSsJJMF3JNATWt5Yc0S/zQsezmyW4Vse2YagsNej0155TMc1qb4zZKwZIvcxMc5V8n9ku6r+NRQWKn8qtFSPf4peNufnjFQZyYzRwMhoSKPT0AwfkqjMfgviWMfFeNrfKJaqqVXecvRBK02hp62VVT36q/hUMcr8xkX09Os2K6/XIQKVfNcUXyrxX/9AEsS42VCAS1Wj4RwFvaRwMb2YHZWhSLK+w1aGz2crEmYZponXnmcqS2rGGxXd6H8WXXW5Z1ebnyLkPzCMCPoeE0HOXI7TeWpGEcfmnjlqJnRCrfCE+bH9WCKNQ1nUah5Ssjnw/am0y7hWJ9wQV4pMhCe543PpXy65XazK5OZ1xZR2B64u+HWcqJvFa1LVAp7oHpVEPAJhMICiW5O18CeWbJClkp5gMNx9ZbvLI4qx8j+PIpMy6qjLoJHiBdkRi/hnioJzN98J3GCqzI1tuH7NkvaZIE9kWRg2tbVdoJTwX6BUEQDfO8QjXjgW7+RztxG4LCwT7H224liHPupeaGXTfnIzq242rmKdfiwcpoFesxtlJirKhFV8jchmoolUAWi/AHh/t6uDOobcMtHRrGiXu6TQVzs5kisQ1hH8ZM7WuHZkJmTds1sTK4ER4zjL3X53W2iuXKVsEyh4twdLO6tjHExds7rXo1UzMsOsx5w0yrHc0MGza4IjaZLaXOJby+5eMxpTaUcEgnGd8Xrys3/Tfu3ZnYOGnQeH4ddHbDmyaipxlsAwmDVfThILrD+hl+SXnAmM+3jmP0VW/6ISGIGWS2XGQd4pECfeRsMN95wufGdVuyNOdgKe3FlH38nG+/NC/UecYAvV8wMdW9yXesx9NAefaBS2N3oLO54xlRaSxoPj7nhwOL3jAHnRe8s9Pgiqpng1o5p/tdKnRUTG/SrQw1GL3liuocDiAHdqN0RND76hAr8pEtuXSlSYkHolbP1WgiOEuF2LFnw7UizPvdgwyzAwZWvma49kRrx/+fMIdvyFD2BjCp3TJI4GKUD5SFx8YGX4O9M2hFW5N1DTl7bhXLoOvOuzrMdRIeGXjR8/FvSgb9mZXYA1LDJza9GeCnYqD78A1f9sE3Ny1PyV5SfUYLsMUG7eVOT7uIqS6UtSU23xPyaNs21y0pX5E9+jFS7DzIY9LOgFHCod/Ss2XFL8t/qLTtASxfoWsMm8lzUr1PnabJMQtEuhAN4knWwMVraQmYMQbvp0SnswZxRkXnmamJls/RVj9aZPMTViRd13bLXjTUhca6307e/lGk6juS4GzRhxnYDOXJxzjDZWvPZr64wWfVNvYbCfn1zXfgd5YD0rteGgIGbBg0PS1YnK3VOQn54JvbmVNFsEafS6ENr25dhu8YhJK3YMlXXg7Tw6xNjpHsfaC2/ZzvrRqaTP1oJx4Vua09QSp/QQAVv4rfZKVkzHqxNYflVgCNVoxccZDIsXz6LTJgWKmaqqp91GsSzVgHBeQzDTZVZI48dY74Y2JqNPgrRt/7XxjXjny5HthRZZlnkfvYHJJcVJwGHH0umoZhEay8u9wqHCfoBGH/RYGAXr1IKNvsMb+okw4IubmdkdyeuWZ2AS0f4OMxNTJowNm5B8USG03B3MYql5KkpdS9NUahF32mqv89Pgz46kaa9AGdAbGRbJ2GlYZ2dgY+uhpwop5APZzGKk7Uz4w4Wij9WaF49mKvAuLLoTjbqnOj+ajExiWokwuvGjboHH/kHx3r5SuPXlBEakE9NrASmDOSNQjzH1k4AtV0Hs3fHQDsZ5l/jJorDef58xbJi8HaMKxc0W+NFh+KZy+tLX2cOJJmHFJWtT8+hwXIehlDNr/q++uRYSB1TkY0K+Zp/FLlIkNXk638agF8X6rIi72HOsiPymPB6wdmc5zNLy3J8E4S/vmtseJ0jPmE+03qtC/t1V9PaX9CXh960dYu+4B8u/T/P/zYP9fI//p4f//evxfI/98/L8S+e83+2/pyH/a7L9l/BOtSBAwA6BnKxzA1INALdx/3/6HkaPb/zjyz8f/K5F/fuBfI/8Xzf43OvKfNvtv6cj/H///Q+P/gDg8/TUUqu2t/9sQCLj07hrplN5x+P1/AFBLBwi0snY3hSAAAO8kAABQSwMEFAAIAAgAmm4yPgAAAAAAAAAAAAAAACsAAABhYTc5NTQ4NGU3ZjgwZDk5NzVjMWNlMzQ5YTYwYTY3NFxFaWNoZTIucG5n7XpnVFPrm2+wo6BHUAEFUWkWQEwoB5CgqICEooBwIhBESJCSIC0IBLBw5KhIDGCA0FSa1CiB0AQUlB5Cj0kIiNQQILTQwdlx/jNfZu5ac9e9Hyef9nrXXs/bnudXnp1nNyxNxPce3QsCgcSvm161BoG2yYNAItl7dgEj/ffH5kAg5W3Xr162fcCa5kRRbvUyd//g8/3Bz67HX814KFF1V6rzn9NL+++S75hcU31zt34gY9fB0G9Pn3/XUmYObvS11VB004rpBuM/E/hQehuptXo5Poz+JyWiSFAUtGm1E/RBbhOPB4G+zwwNG/5apX+e40f8qooOr/VZ0HuSpt/CKwnDNzuuu5Hz2Qus8LF6MdBKxGHorp34mz5bNnOftCOubIaR0/HDkPfpC+SIzfxol60Gl4EDoK1z9Y0ffpkMYBvuJCbfGx/m8RsPh5PI3Tz+9HJ4XDUxPWKrIjp3rwNo1ll/4cJr2Akbg/UL93a5psCu1O/Ky93YmPcHrZD3yj/BFNSrWgU4YKQDJGnRn217QhYrZ3Lz9iVNzrqMbX/4KwgiT1OKwVx2DT30ZP8xaWpjW9sbL5ml28npo+VQeyCEuPwmJhGNutBw60CXz2oObRlNxDfodl+4NVQw7bXtcwRy5d5W6FmeDqvvdU8tL4fd1V7uflhZX/LCxKbI57ZGaU+Fho8bHfBLqyNxVnZ0g2XHUt/hhsnCsoE8KDAE9qzeRnPDtkRnjJuw7+8EdWvjFisv+/A56rSOj3e/PZ/88eRA0RLTPX1yc3mQPBA8nupZ/1S813BrDi9hDI6Brk149hXAeyd78/MLHcqWUtD3jmbZm5T90GR+uBu1F4SCUq+I178ZkBGU9gcNhvWGr0/bqzlQC9aAsCGIjQOGGzdQV1HtKfDHLZWBvPDORoWarTXeZKN8RP9YxXDenPQoZNtDD4OFC+am0qO/lkI5kQuCF+dr3hNV4da0VP0yVomHDf3FzKfg2rmGY73A6uynK8bT2G1nPy2xvHoDGU72cvc/i/R+bDzu4OT77XAvEZg8+GUlwi1Rj+Bb6robNOQqsQlp+MhWenRikJ5uWEvS8UHAEatb63zYy8YFuqGz0ddknxo4euDTqhREmnZpfrn2V1hy+nTtry2lB/0B3Ra9ownOCIShof5CGyTiY+GDvOe2vTjQJfzsBWbhx+G/QprAMKMv1csDDpywZU5W2jAQ8zytkSRhWrMx32odQCIgiY3HQwvacBuL3VajFxpl/c2TdjKBd2F3mostjiffJkQmqnaPzAVyTP2PuIXqHNz+0OMY9Cn61gBv6vVlmFoqPj8LpUA5KLpzELdAO4/SDOEUSFpKGB8PW+yUuAOG+H09aBIfQmBjqqal8PT1mvWZql5Jq4s3N1fpEeoKghO0ZW7KThns0xyHuBLEW3FQ9mZbo+3S1/fO+tfeyYgenaNHbPl3tRqkfssSlRc9Sb+4YF66PBC6zJm/HTqZm2PGaaw/YOhYvdgFq91zyoZ5XwwUib9w/GsfD5U8io9m+9RW86Ya3PbHvGi74/hg6O9eVqlXvpXhZklPSEnFnHuSCiMOmWxjqYtMjnPPmX9lMATsTg5KZTy6Vxc1KwIqdIc2BOZ5Ea+B1aumignYloCneNWkTEajXFD/zb02NuudqDMjGXgoaY8qsC/+1yODLlTpc3/ufHg9Eu8rX9cH/4eUHIqlZH7QHJ7MJ2M4VhkUasbCci7zr8oAj9IHcz+7pjX1kV3nMml9Px6MvrZvEWu6JuVki1Ag67RfGY88AJqQhCr716MlocVK2q3HmHuTCT87fDlfJY8UV2uLfytOVgozWvruineeUuX23tLSR81U8orACv4dl3e/VkrJJe2UgIL+gOZ5jhSlocODgOKLR93Ntys8mwERi+7qu3j8wY9HEifmw9r/ZnqRq9fUyzTrTSYNMNWCvuIFJXaA4dbKcBGtsaGTdmsFdGnlfR6BylxKPnivz83NC02loOzeUsqMk990kr/AM9sVBMd860RVbKOOh9yjp8lxjD6nBg3A95NhK6b2vSFcZPHuTlF5UMcpXPRtfud5HG6ZE6R0qOfp9PiF9ye0re0lomT9mq6u3OumKKSFLTEngVst2G+4Mes52vJaQQD1WJcFJVKHXPOOvujV+d5j6xg6XZp1OiAx6/nl3f2BfWE9gYoejtpTX7D86mWEADhru5xU7O1S3Or8o1JVTyjoztckfK5ereKwgOF8Pqdl7EdZc4oYe/pHGabKrnix61PuAUko2CuWcse6nCR3Hq2fHxNSJA7aIx/WrpNkfmwRFzb3Tap1f4IQYlR/ymq2XjiNK9F9ksXgD1Po0PyalZ8vPJnFyN7rKqk9An6itwv3zRE+6AQuurygA/6CEOfGc53KCVn3JDqzlsS4F4eVtORhRNVc9fIfj/NWK6J5rMrpLpGHHjJQYyc/GU3/2Aweo9DBvjSY7Kutxyvzz8aucXPs16coVrpD2q1qVTOVXoE/Hu0mMvEhy+a1s2Azl7PAWl0TuRPafpGbawJevu8nRjnqRBdN03Wo7u9ecZ3+G1ubK8P4hK0THk+J/nfH2pJsjiaUnnl+GDiavfUmtawoTOvRitzazSX26OATlKhxYf49SQmw3xLMmCOvWDgopXbbFsh5XyRXGVMxSuxazliVeenFQ/sv7RQWnHwaccxJ1wfZESpOKcV+R1fSGP84WjUI4fVxY7eVoRPR0fo+69OSrGaCkx7hRldh9tcvfiANo5XEvIxhf0yLGwre4PQjSYOAfLMjJlrLqy/+ykSXoyq6T7igrkda7l/dGsY6TeRTVz4IwXrSfk0LKgks/Z/ZC4e/ZNQ0Z0c0fBhy/c7R4FAbtH+lXpoD4J24FlcSQi8fiYW1nAzg3r/t7FwYHk4dashKQNyeruLXsDcsV0APD7pDsz1lsd9dRmeprPf6nsoU2/jKuLVBUTkZKWfcnDajB12h3KquW64OloyVISAiTJKV3rS/2g6qa3z1smpt0zkMG5MZc3dpitlrqT9ti1mSqXhbJn5oc3/8MdtF1rk9sgD8I3so0k8eW1aW9AWeC52pcOc6xXZ+eoowMF4TXBIBDV1Z+QPYSmgkvpmqyj980e/5NMBmsJdXSViOP91g9H7FjlfRAYfkDuGU2Y4FFvyX3mTaPYdkwqmekmd4TWX95X7/1veDCl8UdrNyV39v6GmhR5P4n3JX/F85Tipau88BkG/V780XQoN67ca8H9FsYZO9BMq1QBK8y958wE6zuqQUozqQUeYNrngDbS5VmLpiH9mZDH5x/ujzc0WnryUBwNumffmtjAYCQNFixW6f3Hfs0BEewGct//imH+j20R6nsjHnICcqxmysDEqjgbIInXjYJ/MOdIf1FE8VyXC4k+ulUZyPBNgb+ewU5UT1fpv1uUZ52KXmKRN/7t0bfzSptmgxHG2Mqe3Yfdqpb90cIfLLgxERAoDfiBGDAHEjM2GeZcteNirbAVq/rS4T8DR2TNxQ/JMElGTIC4wOC8F8AphBUuRdeHp4oGyuEhzAWBkBkaG9u7pUXKEaim8CW6Ogp7RUZQCMmtAeck3s+H2NcleSddba3BzDBL29CviLYN/t/KAr7XQ/iBXtq84gziZtcPUThr85luxDhNiDAeYvtuDHNM+wPCje1rtjQirG8/KLziqk3oxaFfv7AFANeUcrjpySu4S/ON80uTqezg9RmNGS7LSl4xb37YH7BfMKy5RRcsVeYw3HfGRh+5Yuy8Fcvz0/DJy+I5aJRKYEdF2PwxB3CVc2pNC1fvfL452js+WL1dKlHyiDwxKWftqtnKBBpwaAkcC+f/S/1zq+SfSafBO/v5Bcs+aZlKU7lujaYtoqcMHy9sgDsKBWZ0I+Nq+SjrMOQSjiRrL7sWyuGx3b3Gby3JznD0e1Jc69SMK7GFmwF+5OzvrWi+vEG7F2FNZuCchIt6RmpjpIY+dQBmTPV+C2nI2NTB+boHZkzwewonUGHriewk0BaYU841ZMa37qdOp6x+ps/QEVUg7Srdnjxsc8gEKB6cvqulDT34TERk3N/kGBBqDPGpmM09aG8YZFM58W2sHFU34A+W39rN4diKTNW9gky8SZTqxwc9LzgJ1W36agLGQyNjhAUi7mht0bUKW0uv7aXD7PdusW+PP6Cm0GPEr2iycFvw+q6hnKQD/yomBHouTDT2fM1LCUcW7PlPT9lwZC+c+WptB1DrUagMbUwy2yjrKZh861iutKq8sZUkbAkwWNGqVSuj8KMZ01gB6Kx+ShYz7yvWduSUWrO9d86p2HuWUPCyVou+GvDYk7LFlFFRzo88MkPGIYkDTnHDwgXdoGO7PR+/29Qs9i2EmPNWWqhmP0WwCE39ciA65G+ZC+nIRdfSF1Xr3aVILUxTLICMeQZ60NDf8u0pU+fy2bs43tFpIFejjbOZ7tLG8oDw9/75BjhVr3TG5cCkF4qk8uTeqmYDrfXRsl6V0x908wm7SeL9fcAXPx3na1eqqLF5waEbGNgQidvoVdjvay2w0k4nGdth0vazenfbKgpxScjJN1NppntGW0cZpln1BuzYowFRrzxdh7si8Asudon9Nw881+S20no2TBtndavGEhuLY0g6qQ6VIGoEOk7VcmSnfEjr7EWVRfMU4++sIl4QRLcyLvSUezSrqjcfvTXLpdblWGtjM/GtJ++rIC7KqouBTigYtuoE4Us5TJtImgYdKSIO7E5aJBr/hwpbrdQH4/BF0Imumf/2GPCM6KxlCU6tPSrelmYnvlUy+f0NlSDXO7uDaR0buxuqCCyA/WcFJMzNTQTrW3eUMaJWL0bUOcrmxu+jbK2deZyF2clAMP/3lGCpSNXJmw/4NEPmdfpOrsL0m/J/kXK21fN5qaNTgMSOZ1vxjzBoAfW/3Mxs2vEq+DIbFeFiumCiVT0c1nyp9Qh7H640owS6blxZkBJSDf9sgDC90gDWUcZ3IJjT2t6hl9QT2D408RtRG1ncGvnI6mIC8Kemx6Y5VgZsPkMT+Yp601j/CDEIKf6mkertQ6lL8eqOllrFdWn43I3O8Yt8kGEEL6FM4tCMaxM1BwsE+myMfpflYzhEV1AXKpwjsCvetJOBtlX3j7FpbsNhIMAJqPABDmVpGJU2bNRcSXx3Ts6NB1bxnmwTiZOOp4dY8CO+R8xUisXQTPbe99kTusKDxCpy3lJ+sTfGwMQdeO9jPtRyY42aGUJC61Gyz3P2Pw7Rbhv1T17azdSASZZwnO4RUBuoXbjUJ83UwsjUyMmoWmxWDuq6SBc5nu9q4KC51WC/2Z8uH40ujdQuW/i6MoqU0azCH+BCzc0e9JJQwG6terBERILgnibilIHtzIrgQOukz0RKrCo/F/FGJOj1e4ZZaG6uGzsxXE6+dJrUS1c5BTcEzz/gQ4BfV62QMi2c0028JHbLgGAkYP33/JAuDlk/UmRDBpcDw7/VKXbnLHWEN/YYwCre6IuuNfKJniv6n+8JwB4yqX+qfF/bHL7d+LkTA4ohkOSdZGn6U3H1wOdizyBYAzaynDH5uTxpwY77GxKiSqO7H8n+ZYrEgvhv5Wkx2/qhlhUJLOTM+9kQfr7a86sMpv/J8p5PSOdZQDRJ3DQpdx8oIXxm6VDYaHih6k1f8ofqFEUZIJ/MPskUd4Qt13QCJ8FFpJM5DQMbUWm5ct03numQfh+5/rj8bbmN24ftKL+NhPDf04CSkFkj6JW9y7X1cySwY6+fkVRzkp7N7C0eptpk5eBLJuiXqgrEdqmiuPIhv3w6bWue7qXksIm3Az6k0PNrNPAXICjrn+yBtx7tu7M0enj0RL6IGLoyGuDdHFSJ3AU8GI/WnHtB6cBpwHFNiWBXjzwuQxP0ikW99JNlyoofoKW5IzZo7c/qXOvicJEnI4eJ2AxO8gPJh4G9UydRWlOSnpkRxFGw1iGsQhE3oyRw4NkGu3Knlt5saeduD58gANYU60tjUL7VbR22ks8yZVdrsQrX51+LuSrR6jty5Ot0heIr3NZBebsbMRomKiIiop943gW02ragBKn6NIiirB7ZqnTI0XBN2eBtPdkijrA37tuuOLn7LHtAB0zU7GnIWowFtWAfn+9Cxp+haji+d/+LeByROIFgiSzjKcI8KSsu6ZlXXSknV+vXsPOeky9/Nb2HaTMkk0xQALgCNyl6K+ZYzB0nfPKDns6Sr7SRJ+TIBaUmIIADYhKsUfyqbC9+aRIZDjtO4Q/fp6DZXFvH8XTXpPrqhBJM6AaNFXMCsAjqLhx5uXGJExPc/7AVvf+/zwOTNf99vvcvI9ytqzOZifcMvc7ZeJNn5H0WU3OmS9GEVqKoy+0uPox0ZCFdILqEy9g3m70AozjlDAhN0xB66l+JpNu20z5rV3qoXvvcnT1hEEjorAd3ETUcZ+f8WMfWztpolcqYUznure5sZU5lizdzy7zOjGMg6AzNmzF8xEkGXHPIhwiW3FAbHvegJkaW1GlBf3atNknkyeXeP0Q/ZB2rwtw6a5yFgnSJxBPgp8cieoDRftou8xsoPZ49yzu7iX5V0xfaufSdYK8c+0MiEvTwZW+/bB3V+/0my7Xq2Xsu0zdr98tXHMG3pM3JQsN+gJxsHmprNrclJkT6jYgs61ysTjAR2X2T3PApIPHmX4vZgVeTh7oeEHYVtnCtmafioa7H/jV5G9uMn48KnxioAaTO1ybnrcLiSN/o5dAGNnEakiO4RuwVvJYOXHE1iqSTLzOab0OAczUE36O7CKoLP+anGfRGlKSBWvqMoOkF4LmajzxlzsXoArpI1Rf+yi2ZaoaRZGENOObxZRFt6UB1yW03xxE3Zs+VBjtmFTOdEGYKrvMUMZ0Mc1DNWGNx860bIRG3MG61g33OpoQpZJIyDvrJ0Ce285PTEZL3XEzX1DpgB1zu55Hb3QUU79VvSfkO98QF7AGzlRToUdQQN12HV387U9glvhGNc3GTQYFvTbfam/zx1uApudFwXDj+e9MI9ivoS0v9omXGu7WvPLCEcHG94gPQmSwyr3daU3hq0MRWVd/95f4d8qH/jdJeq1Zb7oqTOXCtf/2QCMGVLKcn9dq0igTD3CufYDeGpcqP+kG3rtnQ1yR1+H4y26i4VIPe7vDKjUSUA5qkJkBLEtADe2el+3rKMx3NPDqIeKoEIyAlaqOydSwpXruug1FgtT73QTAzUchDaUVmta1FSmMsCn7y/ukxcaEd3QLAbPTXv48T7198Ie23yiav3IpaqSoEEAT2WEWDqk8Hbk4fb9iT3R16gbM6UMBHtHrAu0LHz8J+hzyV75+iMPl46ZyPperegMan9fgj7dN+0uKp9UOCHoXzzcnFt5xhwNPR8or0seFeIvppKb7dfkVMgI1KrFCyH1p7t8xIZvYNPJKPO2xOi1YJHPJWmr0oymqSsoaWuvTr4yh3pcUSHqW2rwWNKtMi8an6IYtzQhiDUdp1VTDjS98fJ4ip96k0sWunqysBdoB5H3/G0LO9F979Arfw5HQ/IAmTospXU0sNM9eSYjdZBO0srXWx2JUynK908a21rnnx9y7c27tZ2nzWqv6XmEBKS4pGEocL8tFVpPEFahgUBGQeRlzkyaE+49v2gjVgnwQU0YVI93haSAZXnkCBsUBqFYN7jSpl5lqZ28Zr4E/Da8BhfMPRx7mzAV38wfAKjBE8AmSbz+0nfXfAGPcaBg+MPUNpDrXnk0T/aUzpw3wWL7h6CB4HEpnc22x4sk7j31uMxwRXdyJt6kzEk58HT5xLsXLdyS+vYexZ4RPSADlycTXWPO7MwKrjXtaDK3VPuWlx62BKcn4Tf0C0fZ4dnC3kNFcJ+w76fmWP5hsXcCl47Y3dILnFFGF0TxZb3QRhfCKdnjbaZYckrE1iqQamG9IdyMpYTajSy9xY4rrfMtdMNfjsK2ZdZnrb5CB3uUrWfusmmnh5yGJ43Ran5dLl6oDE/ixKooGcKjeP24U9UloF16kRVCSooFxHKtHiAczE6bRnULW4y89vgm72usPPcXaDaPFm1mjDKQiD1l0QR+4TdCMCHyIediC+tFoR53icvXaSbbjPUqUG7JPpyfBq3m8FMtYteT6QdB2eiVCeoOcJHriJeoBMWdXmR5ce4ruOuQquCEsPNzZqTgilkNqln5yx2AckZZYAohYlmPpi1QSlJqdl1LVemWFT0sI3qM++poGQfrAPermCpubVkAXKxdndXRnKybTFGVlBs1yrJIbRUFEcW/i848sHDvHfP+J+kAKPFrW2O50fXKJzVLLK/RHxXRO55HEqJV89uSdci3q0MCAX4ejImMWWMV9xPgLxGtmsyBUEA8E5EJ1M2rxZqxhA++mwJGwrvvJffpgswthZOn5Wy69TP7HB976AFaoWVBwm1tmsU93PbbMd8MsRPbq5EKhhFk8KVeDCIzMuDkdOlhHZ3lMUti++PutsR+QPtmbfcgq1Wn7iyE3202Bc7MlOh8RPWvG9OAqVISSw1f4yKpyl+yw9N3ZEa+ye6JGLkQjDj6KpA3yZoOHdoOGnJt0riQdKlLLTLAE6pNUVolqX3gYMYEPKU/3VYVAqU2MWucIgWYYa5Uc8E1o6+64yk2Bhuz9cjrSoHKSW9znRXeKvLjmEnuacHZ0YClft8WPwUkHHI1u4JDHaTe/T1D9EnXeJlYDGQ3PMZjoANCuUnHfBU24bdddTckUHczBHsvBePHmsu4WBLErahijGQtH0uYLvfww/bcNHktkxgQRHPBpkdsBYtabaKIoEsriXUkvItl6XRKdZN4NSPQmDqsjAOAXCoOYTTZ66GlVyYS1HKEExmvBCPGZyVM9egCK4ahWx18qrN+HAKF/I2/efvvsuCBN3Aigm4RZiq3rVLNyW1MwaIBzNaYlLAuiwh6SkDA/sz91aSeJns3YboKKIKNq8MQYDd6dY1uBx5KQoGsT1xsayRXL3YBEMUP4t4IEZLoY7q2vlNI4F/oyeXwJ9QuPfZOkPJBqHJ3Z0DeNljZsfCFoN3yuPu6T5ScbKPC+OEhWueOjZv/ATh0hX7zxpv3WSgV83Fx3Ex/RdZocGUWVXQfDR6zuPZggaYDq//oTbHovKeXgto386f7vTYc6JICroS7R28iG2om/cwbJhdgHkZeNsXHxFnqefxc7NduVeNSSQTK7a6jBk62khctDQQ987e5nJu1PuwbnTjHZCctkEZhfSP5JuNmrfukpnWB7kQPG6GzUXKJPtUYZwXVnZ0T0N3bEm8ab20KpZPax2VOkDOXSSCXOtoTA0jsB6HVmDS2doGoPMicNzsX8fZ9ybS3UZmx23K/vxXXkrSdy/I+1s5I4cR25srs3VrMMXzt77zU70+fnGuU5x873bVlwHBh7gTdfop3zsjnarz8vOZkw0pVwQlpOaxsSvtXjbB7Hx2uf2cS/nZs6sYmf807cW1hXfhpRH9J9rm9IapjEASqM0kPidF+5JbY0ZWNUtRGszRnS2vXZ6q6Bi5qHUPXN2bgobeNdWiznd7c46ukbrT/hKPx3ls8hKJHbRrljl2RIzMou4GpLryGyOfh7tnRrs1Z8MZOvq8HWDtia6MPco7JjCU8+QnePi9sKh7hcg9bRyiX6v2Zqa64eXWJEzQI7o4lLEcDrqygDTei5Q9yGh9nyWAiha0gZxcxUtY/IR5uN0ybC+oL4JS1p2/HxK7uf9TaVKHBnBbinp2wm5t0+XpOz0VlFbaybQ+f0EHo9vKfRBv4x+rFNfm15t3KN+vkFiNb8wBFHpL8B1By3jvbvRiPdgEzTPcPlVisNIkWo+tMnJYv3CNmb2360w3sjes+A6iWR65Zy7tdhnGS8XiWlu4UvjoqCTvt1VeQK/RRRPikUuKYewKj5bKfR34aaH6KQre8ODaW7KPuEOIfpvtAvRayACi8j3JBZLEQeojdD+BC1Aq7Q7WkeReHlSASggKjcGI3KpT2MJNsynHIzC3ilwv6HPIBu5gRImRQO/aiSLOq6WZi+0fAqU1GSlqe/qJE0QKYJjAYs81kmwWVnwZQOxKVVeQqIvwUVuXUAP+HxXzIA1KuCMtEJjy6lhf4V/PUNeqnvlqftIUusb0EJCF6ca6p6PUOAq4wIqJVrSxeJlq10I16qvR4oAaX6qX06Ge8jeWZoeGiqpk84nlnRJ3p0TdKTf1YNjprHw8w/yp1UsBt25Qsgpmzvs1KCfHHjz1BQUlv32E+DvA/wj2vlzeZajSdKUkabYptAUr2BsrRmu/7ZadUPCheGZX0iKti0dSuz/80369KKfjr47seQma2IsxkNajupv/YDlB22MpKqV4qdt++imc5Xh6Tqmu9mIBdcZrb831mOQidLwqX7yxNMZGZDzVFXABrli/8ylEcpu2AhSjMswe3qDueTz1O0vFB5Io0S5gR/0KEcLPAxfVKMFVYgroa3aoWj0tHEs8Vlb+LzAHqtGIq22PXAYiw0ecqC18zrf52+rIiREJ0F3ONNfawYi2oolPo/26Ra/Nfoi57bOoRKK5ghdjRxB5/t8wHJUU7Kxa7YPmAsapWLesRbypuVWL7ShoVF+o43ZBEAXArfVeq5U2n9oNFXj1h7dmh4LExjoyexH6SQJY2jlz3RslpY/q/L/C5KY8mxCCp6dfZSc8jXzn6YFs0B70WxmhIuEqEFQo+iSn4DTe26hVi+lUSogd17bOCw2hJ/yAUOCaS0MrUb+CY28TwzSskiiIH5WAtFUuK3ZEB8N4a+QAIIm9z676e90qTafJ8m7Sm+5nilLjO85EjuvCi3HX/aAgugH2XDXfoytc4ApL2G/v3drr3UEZw/dQt2IXDMAhnDTnykLrY0DR/NQzN/fhxOEafqOyUm9BEZYTwvMq8JsVUUrXk6zfEOUbtf0K3gzQWOovVVm2XVk1nrzu/5GDZhd6BhRFbVYObRQEyNL5NedITNphkwrL6Jlg8B5XTegVo4QPy6JhPfGq/RvucEC6vMLGAxkdj1uydAm9x0w+KnhB2/lwFk71xe+XZ+fbPQNtA2+tMardkOKRQi2/WV2uye1cvNMrabG4t15IBDu9YmGNqgd3bU7oiMvYr2wT/MWCb6r8d1B0+5hpPcVorNfIJvdKu3XPo5Vj5WsrrLp5guG7fedWX37oOlm457Pr7vTbMjO1qLPw4c8Tpqr6XZsOt7Z2fTo7PlpaokwWh3iHuG0MHIk6jO5Jp1Q1OZeAZ+PHfdP3ZAtshXj1zUe+wxaddLyNjAq5yPHJSs3FLd1NaLUAa6HrAs71AsG8lOwTwqJMZVPf0NouL3/J0r2StLgAGJXjEjm+zGiTsYhYj3g1KNGhAtg877noGKNYyzy0DZsw6y4u8ObnzffWAvFDLJbbRAm6sTJSeQ+W5XxL+HeBZBD3xQoZs8C8v71z0QsW2h7NDT/cAuQ1EFAE0LQD3u0GXymY7+5O2gTRGhzIozrtAn7Gi8kQnEAjYAHDzIOO98jTsEAhkcxwK8CSIbYDrifomAvJOmHXJVwN94AARhMGAmMJgwpj/Cv9fR/414X8d+dfr/5OR/wjwfzHt/4+F/J+n/d/9/+/+/1+nPYFb2fOfBQconUsroN+P/+2I8PG/HfmP1/8nI/8K8F9H/ifTSsf92hnffy1vNPOPGhDwu37N8mqR0Z3H/wZQSwcIJ6XT8fIhAAA7JgAAUEsDBBQACAAIAJpuMj4AAAAAAAAAAAAAAAArAAAAYjE0MmFiMGFhZmZkZDBiNTZhM2U3NWJjYjczMWEwYmJcZmV1ZXIyLnBuZ+2YZ1STXbbHHwVLFBTxtYCYUAJIFSEgRZoISVRAqYLUV0jACNJ7ExHGAqEImEgRiSCJAQViRIQoqDSpgaC0iNJD6BCKwH1w5n6ambVmZt0vs9bNp7P2etbZ5+xzzv7//rl7yQwpuEd0DwAAgmjUOQsA2A4DgG0Fu3eCkT6fkVkAEK1DnzO0Cunh9q+UWXVV7Py+tkvGGp1yYichPYbvXKeQyKEdxgcQ97bfi9kda5IldED2kkASxMzQ+EGsgLy80G2MA30gEJd7Xbsfa1CjFZJbeL1bC8ub6hdkTNKrF6m0jUIAyDLc/MkAAE2FmjrGxmJJzk/25kZwa6vY5q9RfU6KPztqzUvL98e5VnWtXHZ+RfW6pnUztjwq85YY8F5oH4y6f3VkDO76k1PCUI5e62WbhU3rb8zic1Q6oEfNdg3yAVHv0/H8f1meoJQ0bqyvNSFhkVbRUJ2gFznmbfXTWrxC/fWid7/mmoZp3U6UaPquZG+JkYB4vHf6AcBldwLeJnqd49z06NS1xjjIwcbOIsum2B17G4cznZ1MksTsNqsnyJQJ9lW6t1JlEFf+sYYXuXvoVw8N15QLrn6uP5idzu2lZ6Yr2GaEzo+kG98/nE5nR10d5gPi8Jv+Gyujmc4bc5nDS703Tx5x8DG0Y0RFCh7atU/sRMK+4/KVwdPK5vrrAXZ0b0cRnaAbBJ1gb0GR0PX7J6ufdyVYnbd5ceXytP9wum2GOo71cG2awegLn64aXuWUnAzuD7QNnfmwqwmsipPe2qQaWIcNRjyeUlL91kZGuXKyVPSMMFRYNSd6Y2VuLB/P2lN3Da9rE13wI+X7Kf+RL3MU53WyonP1uz6/JqXhvASo/H79Xz4V4wWPG4ca0poCux2DLXxQKg0r7I0leuDzke8fbvOtJhV2hOwBsj7MtHff1jJSgPxxxDnCN3SxyxbHNpE/zlhpvnl9txavz59z6XyscRJ/Upb595Clb9imHN3wibVC81wnBYkjjgGX1wlS2zC18YI0yQ7tY5ifnxPVy9/xBsJ1IyXkYcAM314YN5FkuijOkL2h6PDmZYsD+hKK6bG9Djy+q0af8FEL+X4tWqOd94xrjOUly7CtxYxRh+KqH/cUGo8H911WEE2TMZU/4hTiSg0bgpa8mztP9SFpqVsGOEfMfprjOG++XYoqb703jvjEW4MC78UT8EuBWnorQ2miqh1Hia5pVqeVqxY6egpnwRvAcn1opaPamQpNls0Jearo+LbcRt/kwdHLxy7JmmVd4TPejl41Dpr8epki6XnRtMxz9ZxTyOCdntFT2Jas0hvfSkVNerpnPNa/iRpoC9IXTj8BAKxKRHlCEmtX8HZUQZMJ5jlc0+05/JbEB6nBwZnBWvUb8EsOfg3S6i6KTu/enAELSbuFMJSeblrhT7bSgYZ8vzU3lGbO+rnOY5ekJ49UaXXsT117nZA/UND2emeB2SYUvAPxl5bHFsRvJv2sw3cPJEpfyOgseilytqENTRYT0W64kc6fIEAZwtaga0zCzmGaidbO5tZwpq+a0unoUSxZoiLo1/IsjSGVSJkfbS05lNEnKzH8LNNJfvrdvFm2EtPr6zP6HtRBk1X7NT7gaNxMu72uB3cFFShl6XpQ5nPiMdvbn0JHs23jBY/ZPDY9CDfBQx0poqFKefCyP4UV/YamEYUYTZkq8QpkUhw+LjMugz/ZIZxDpbMWDfwYAt1DegSttPFKbt7zXuHp/uLLK0CMhLCetvUBIpDqT5gi5iVbKeaEjhBE+W1KnPotx+vDjlNsqOT78cO8hVD4Q/gV+LkHoupkG11VinSkmFbueWSUeQlK/hhEuSiCxP45Hb0Z7qXXzC56dGauXmpRp7wkvkcpIoASvxsGqMTVIjkVC/6ksBSJTNR+FFlC5F7FYPyxxtHcaKdWrMyXkebHuGVUrYdT05p39cqIqKaFFvpr/YzpWWOy2NXXN4ru400Jqs8m+yrKWp6ufL+9f0KVKxJUMd+iw1FfqbR0z6dLd4bvla3ZBQj8uTzG8iBKVXa0PDqVbyPfYUCUe2VXJmWJUeuV5oTBxeEX4S59/q26w1OV08WukrhAcE3VeP5E/vtWFzsciDvqOnRS2UzL1B2NczkCTfB3JPnUwYyLtPWRxzevq8MHC6pWU+a5leNB5Htb+/pYgyz83i5Q6bbYAU6gJgzveJyirissZLF4VC8i5LhGg8CjXu9K6sbFma/0m87Hn6I/kSAwyF7IKQhCK1c87Zsy4UBaa72Qabx/aQsyPqT0ud0Ak8rOj3RMXXrfTj1CohUa18oBAhbLHpGaWA9p5EEDYUnvd7Of7QkoH1RMfWMhBOIJNfX3IJqqfdLoNpE/9A2h3IXfap2LHmQBiOQ4XwNt/CD6mme8R2nJBT3ZbTKC5JUsKWRSgIDIOli5k6hCHBCjdlRvlanQfuYJk56yeEZVSlohRcNV0uhk0RWScOr4K0J/qkwXfxoiu3ptqnJxVaCXZAvfm/zsCNxQiokrG6hLgEVdSbgirGFhjW5Dl3m2qBspVFkj3i7GLXTxJCLAHnAHvyFgTlJN8XxFWEmVyFCszNnAL0S4yfbw43/lSDP9vbafK/hRoA+v7BzpsdIUvliq4x3vpPowraBjUiTNTgmiUaEnUfhtB7335floG30udc/TUfAlGoAvUejmdoOgLNNck6VQ9EsU3qTGKBaJKXKLPx9/SdVdo5lkB4NbpyBSMCWZC4luJ9w3N9YDw7xXz/g5ZtiaJ1dMV69NFFdAThY9DZgwGkfceR0Z5rPWvlG9NA+8FxGAZUMb+zEPEB38xPGSIgt48tD05GzqPZMaE/mjN6tXMOYMFKbJwb9ZfXi2DqY/foEkR7NzUUSuGvjhq8J5GflI/JL93XEva5Z3d2A4DPCJr0XSX7Zzp806XIhFdM8zzZMZXr2vu+7UCZ/pIBHvoZdurNTCNi6taZZ6Oizd3NIrQQWIHATh6ZYYR/g1cNUcGV3QtYRtVAJUdqfjq6F963Zq+QR7Ha+ecvuG+raLS7caBhQhsuPDKOZ1srhITsP0uKBnt8DdhWcl7zvZw6xtW+f8VhC5oJFIi1RKroYOcUvUmSHha/sK1f5YoMnL/3VeUbPwxz+025QmwzmM5ZtxsdXE69tiJC6tjJnDUNEafhzc/gy1V5Ohzh/2AEeHQKUSHuYyrcM5e0Xqp0qxkhEBq8UgVUBg2TaHvDarenuO8Yl4azHT8RtfBrYBLS7LY39oCqsSTdp/TdqcGru5PNYaxCu84LwuB16TOLz33kB1VylL96uwzlCl0dJST9Zo/VuxiqkAqzNmo8mom1UK8Y6AS7ICyCxDL+yJ+Sld6DKxsKDC9XHzaHtQtLLeJtWBdDExN94cBl3PbvCTN1IrtKeOlUfdndkG3P5D763uo2N27ojKppzwqQr3ofqUwJX5Qwo2DwtzwsiTX1/lO/W+OC/av2Sr1VVEN10cXhNoKrfV7Qm3A2IMn0eUn3aBavo8UU7P6ceWWXpp3Md1vTtpdDI79mzhYCIrL4vFo3nPscY9wi7aT/drf2TCqvphv9u43sfZHlxJ1+BD6lV6Bvj4FqyEtE2rvEQvr/UcK6jCk5gt5VzXZ+seVUHi9+PcdxcxJ48LFoKnMZi/bpjVzC7d3MKm8HirMIpZuTndS/Aw9wNJK1eljXqSFHniBM+DGhVAvKsmJL/VaOVhKY6YYG6P9emotV/zreZ75LLJQlQj8WbFRyMSm1w6m/WkHarnZ1qowvQ61MGaaR/gU22baYeeA7coAKPWCn2781rEzzOyTVazvHhlFgSwrtxEVkxyt7BBj8LhlcpQ57VROi9xiIdZMqVz7uwGNJtqkdtrH4ioTbQOkHdCJLeAq2J1gtL0UM6ykYROa3xhV7aRT24rqnsaGsmujnRvylAKPNw8N9zU1O0c3X/wT3sGdj5Hpi+CLffm9yVYAjr4Y62kR1qyey3b62s3tmitzEVvfYHpB6pnWNTGr5XhI4xlY2pqX8jPRPelyW/uX1+66h66uwsa8uQGu3qdBJRiW3PmvmFzu/yLMG6rU8uzPzmTxKaTjHeKV1+/GA0fmlfrCh6sueMOcvTmbDaXuR3A+g7nrw/qgmThx47kpYO8yWo0IYte+/xATsrkwYn5kWbKNvgHqb0PqhZZV2m2Q697vSl7U6QRWZq+TzWoMg8R1g947GiGg8+HHTRyalRqXBqnuLJ45wOrSwPgIv2YpqcXIzIDOax0ULNKfk1i9SmcB7+mghkK7Ij55mgry7j9gObeWmQSf2xczEhebvrFsqfjILI0fbx7kNN2niyWJmuu/Pj0zWKJH/joX9dCx59lTggQcn8NyaqThpzs/HQHr3F7aLpGkhTbEmWQ+CgSI3dlc55TCqrBfO7TA1WL/iVvJ8hzoIqxcGp/pE0nh2/h1gCvTn/DtwJku4nUqWyNSj6gpXQmZSfzxWzKHuMwFWET4jcFbunMV5DcrxugpOEKOa+VG3JUfEFkZuUR+9a+vrqmrun2SFpCZrrVXhKiAoHfP3JSGURv8nT/S1cjEd2wgG/lnkx08wuqxTatkBmX7H19Vrrapl07gHifZQ9S+8KrOqhCdjEOutCqt3aDalVeEtVTz2EWmk+LyDSEg112RPV653NRhEUValgqEmpXXKX+hnQ2dZCAyA+y99bFtGTZKaiIQBvbWm7v1wvpYAwyaBeUAR/RWuR8cksy2uY0l0sUoJFKU/agD8voRCzPoMuudfClusxugZ7LLNi4u1VUQcS0l27Awg0Qh/BWKh1jojrBUy8GparEIXLZS9cawi190frnybIVGxWjORTeSpPzRoevvTKgcq62DvRDuHRJ16e9IzdNAbQ5stj0Zb3P+TAjVbEyj/anpb4/P5de7yKDao1quEj4EtXwJUOA4XYC0/vay319dXFxEVEyokdQT3P0V1NME1Fv98JciDUlK0COI/FQKuM07n5EruD4b322aHik4WVPxQRUFi8a5hCUxo+g0yWR8Rfm1HBBcDHS0/awdfB+OygcvpChuII/mTkz02Xr3JWcmsi10B1/bee4pnKBUl2tBjaIGmTsOdYA6tlT+q4VA+gIlZIJYgPhWwfXCaJEMEyT6SqYa8/N7+UhpHYC8R7LHtA2z++TXl/dnyDpcq+yWRyPFneNCxh2QBi1t0qnOeQ3Rh7V0za9zKXGtvXerlonDpAP9jvhuBwP9rECJm9sqUo7excQf2U4nz7T3psi/VXN8llJI3KtgtU8qG3K4eJQ7k92ASqowfySXWHRYSfsYWOECaKdPB9EmVpmO8XY3MhJHCaGY6qSWf7r69X98tDtuwGB9sa6IquDpbzGT0ec+zhVvZSjKXKlsIgZQ8dD6l1prJmUgs4X5T1Xr0yU13o5p4uBqlGLdE6P3RDDsV7IZToGfYupRRZ0662O5QfmVygKsUT1SjNQhc1DOy2eeW7yyqP1AJ/DNnqluy4G0ZqVaVTDPP08ceZ1NTd/Xn9wbrlYeMFPDN9bTHbyQM3noqU4ADBCRAT0lFZX3fOdruKxANW2gQeIrGqwD7pP9VWof0TkfU8z1ytSyNPg3A7YgygU1rbf5IJCKQhLtJJLguk7JSB7YBv0gTBc6FheglnR9VRdF2JUiswYqTvfzu3F1bajqGWPzdN8W3k+gibVdgq8jH5cWjdL19beyJB0GTG6ZUWLayWp6amsbstvVyr83Pul6eoRkz00DqlVq/+vJWZqixIGegRu3Rh4V7Ev2k2jsXK6+ioP0zBNnTYdq1emF9ksqDsw7Rv+MhmjEzjRWRrOm8q5lOyf6eCHtqsKCzQXH1d6n9V4nrJ1BLcakfM+LR0TEFjKpdnBBNhSn3hv16gH9IfIPbu3AZ79Va9pWuW+39/fKgUbX+m1uiTtZxrddBtNjRtfLwV/bl55d5Ln9MbHdcsIhGXYTrduKJJBTDocjzer23KawUQvqkG5dtDkFYJueNC3UvcLrZGPcae9eqxkzHMcCi4SLCiyW3ZXUDTU3MlcBd0ldf+ueodlav+NMsaXgapwnam982vszeozG8s/F+sR/Uho6LllIAZ2dtkj1mR7Dei77PlM/L1X5oZp5tdGvhAC3Zkr86OZoD6lg/Y2791cowLtT1VQAea22sQ9JBnGYVEpulJrS1xKFRTXXawE6lek+Sd46QBSTwEXgTiUoRmx7EPQiwwTVIOo28Uo5qbJN4y153NoW8ZkEBRZg7BeI/fWHF33D7E73EExc+8iWy8a5rqm8N/iv7OAHXqk4npWUBKslBJojKLs3oX4Olb+BFskpSslLs5Kgdja0tkH4krWgp3nDVMPT9CBz3tXDGeIxr726rWpvXDWbErL98fHrbaTJq/2O2kjstDRvdcZj8jD2JyP/bS6yMHRfoCdQvH+YSXyKF5My2LfcW2rY0g2qFL27ai/1J91heyGKBPuPXZKxUTi4xIQ6RrRo/OgEkygpAzhvCulbmgv72w1rFnFTM1eTo84RML0DokBXqyZA8CM8z4Y934gTS95P/TMV99l6cTnwQOhWEHhZjYh6rFKh3LZnxY70DQp61RWQRfqa31yM8gjURYe9dBTFdEt2HTm8gLTHJfu3lPuuYglXlXjfyiRjXnzLPDwxWgKDGQDK70enl3Dn87jhfXk/NCxYLLQ0CA7q9WqT4D+5fHpadJ1Y3lpiNjWHy1UC3jcg2Onizdy8oiKn3JcQb3AIHtl3N4t/7gfeKAMzFq5M/tyvkn6ASmTh6eufe4M1Fed7DhWC2pHRhweQ8TFozs+EqIeKBI2Vjkl3Ys6HTOExdN+ymU2xITgVUOLZ/UV/JnYnNCCnUm44oqC6owJY1EjJjys2zG4y7PCE9HcKlBIOhAIAuaiQ82Fmk93D8qGVc+0ZOvg1OHbpNNT+bO/+DSsrK/xuvNyHdhyFxew82cAFyFQtgzMbnuQhUV+oKQ8MbQhLBFleaseR+1K5U/6EoA2Gttigpeutdff1P/RL1CCOHR3IXxolT/+V7ZcmcjbBqte/syFGLjL0DzoMdItr27BSiDZO959Tlf1hZpnB8kejR6WVvOxuIt2OT9sPAzqfepMe9wdK0nVNfj+pS9BdmUY0+NJnktBnsXmoJPTX+y0pJ1PAevQkDPTLtAaEPa18Gzqy2Tc/MbkfiZ/Mn/aEs9NohRRhjnSF2EiL16B1FNzlf0At34MTtRVxGhmGIEvTkJIb3Ui0SN6DIsqsC7EWX7ycL6Zf5UPFBJNWU4ovNxtWXqtwm3pvPxJCGx8DcWuR8IiO0FIMa5/fZPtRFEKdcYw3K7INhc2q3xpz0fiukgl09t+tx96URFfJJVRZv7WUyMbF+/1VunVQJ/sIInwudfzmk46yFT3a+qKdqYxaZxJgzWNL0HbtrSqp3tFs//WtSeUxH2fwXkshn8yDghXT+uaYwMLennbgSiDwZ8BVtLVrcEcyhHj5d9gjO311a5mVDkC3xVBSuZpHeMTBGb4yBELSyLcksVFnoFe7cBvJNgFxIBWYzcMAMD3Jx4BbA3/cWRr+C9G/jbB30f+9/O/j/zTtP/GQv6DtP/GQv5///+1+4+ZGWQAgJAeAAzyAQbLAADal63hP46Aw38c+dvn/0rkbxP8feQ/SPtvLOSfpv0/Wch/zf6/J0xHb7PJIN5oO0fxBMAf2tjsXPFZl9j/AVBLBwheKJ62YhYAAAAbAABQSwMEFAAIAAgAmm4yPgAAAAAAAAAAAAAAAAwAAABnZW9nZWJyYS54bWztXNty27gZvu4+BUcXO7s7FY3zYdZOJkmbaaZJY6/TdKZNp0ORkMw1RSokldh+qnZ3n6AP0GfqD4A6HyzaykGZXEkEQRD4/u8/AtLxw6thFrwzZZUW+UkHh6gTmDwukjQfnHTGdb+rOg8ffHM8MMXA9Moo6BflMKpPOjQkHds+Th9887vj6qJ4H0SZ6/I6Ne9POv0oq0wnqEaliZLqwph6oT0aX6VZGpXXL3s/m7iuZjf8IM/y0RjeUpdjaIuHyfO0mlweuReOsrT+Q/ouTUwZZEV80hEcpg7fXpuyTuMoO+kw5FsIrEurhZvQRO3di6JMb4q8tt1ng/ehJQiq9MbAk8S2HR+5hR6bcZylSRrldjFuHtApCN6nSX0BfZHEMKZJBxcwWa6EHy4uijI5v65qMwyu/m7K4qSjRUgJ4gKe0FohBbO79ncIJyFRSgpKpEKUcQkgwoxhKhQe4hoRjQTlWGrG4KnN99y7zbtzU9cgzCqIrswM5kGZJgsXz6rHRTZrGhVpXj+JRvW4dEygTdN5fW1fB9CVdpWP8kFmmjYCgrow8WWvuDr30FE/9KvrkXvETag3eFJkRRmUdqkcOjSfPf/p+tiZTnsh1we5Hs0YdtDpfayJ6+E+e/7T9crS3E+tWTmerBqjyWvSKrANMLgl8HTxWdQzQIhOMM7T+vnkAohz2SwV+wf+Mh72QHPmqTMdE+9rzOOjJdIdX5oyN5lnVg6yHRfjKnhnKezf5SaSmDgdwqW/0UASWXH9FSbgWxMzKM1k4l7vPGDuLppn71Lz8dFkEnYOFcw1rsGAwHpquxar3zXolv2WRLVtscqTmaEBzaodHxydprg86kzNSOEswkT3m/tzK4P7a8nhaBRlo4sIWsJm9ll0DQZifj1uwBdFsrjKKAe03BJATUd2ACuPkTFJYxTrhsTBCIZ0KjE3JYdRFVyB0oecMCGoVJhJpoCS13YAirSUVCCBMcfINt/4cd3jXrOsJXFToo3YPVy3APf022hUVD+uwrfIuxlDQV5J6lcK3V82vYv9Yfuy369MbcHogqbZ9RP+kaAHc4nADEpMCEXUvbtLQ4EYUoKCDCgnnO4P+ydfCGkxCcENIUKZphJxxL3UQqkYRRz8E8FcEdUSubgYDqM8CfJoCJM4NwPb7hBLrXMPIjRjbxBhC6eHalxPbkd+zGakFWlUzZgTvKPOot2vL8C85qaqnHOq593QFlXZIDWOndjsx33lNkO+C25bKaoJxd4yYAe9DIlgHIIWLQB4ySR30AsMFFccZKSA5ByrZUe3ZcHmbe77VN7dpEOIoOK0nmKeWYI8y2twPsYZ81WfcmnMyDrzl/mrMsorGwr6PnO+aoP4fypq8APbpK8Bxh/++2+4IOuocNr03UqIRfU8bWsa58UtmBO3/ej5j/tLG+sQK8lAmRBTEPw1FoqFzKoY1VhQITTW99EzF5Ft1zKH8ByeCzj/7z/bIXYhxBQ76G2fh4mNm+kBRSUEtRC+CohCgcDiVoVbLwBvJTGaRH4z/PGO+OMW6hGV8RzEk8YsK97/ZPqZuXKw7kr29bbuicd/E/C9draud3C2bp1RA/ovW0BH/i7GKJSCa60lI5JTzA7H1u3g6h6tiD9uJ/744MQPZk5j8F7axxhUeFfXhSGRBgIozIULmWnj7YgMsUBAC80Jgfjti/J2RM67u1U6nLV3d2efxN3NRfvEZztkNz6gUIC2I6oYY4QxrptUiYDOUyo1YkIKcCL7doZni3ro8H+6yRn+0soZ/nKbM5RffeFaISzjnrQzhsnhGcNlq4eZkk4B1ljJmyZPwMIaRwGU0gdkC9cT4HSeAGcb1M+0o4E5PBpwyLERZlIioSjjTHifiBUYDiHA9QnEKG6MIDhEIRXk6YghazD54ZDgRZp4Z7XFDGwKjF+0cYIvbinJfLxkT4dKawyqSphgiGjeiDbkGiSOkCCaacHEvepR6TAazBb3OM0S7ADopyBqDz3v66TPhJCIGtSPpDGxShKCTCR5T5HkzXlt0pyEo3zgZ5Dmj6P4clAWYxDfgnzBC/SqIhvX5jwujcmfF7EvP8FyCVVugRxZJ3cXNdxBTot7ARMh4bZC6qdXJtlM3dsgJssQR5HUnClmZF+hBFIWHuPYUKYjgSIh2Zs/pvGFuTfEnHoOMVdP/aIhpssQ9zAjUQ9FUb+fJKjHRUQN8DfuSYoj1Ou96ZuxKe8NMdW+JqMk/bIgXto0uJOVvP+GAPMx/tYMYV9FbRUKMLBIQTAlIaSSZFJsE5hoCnTStgSHm2Rzd/t7NSqBBXZ+k4ChE0DjSee77nc4ZOr73wckFOr74IfAp4H/eAQtTbr3z05wtCKbfDw0ZRrPIpDlNKKLRSjB40MOLMF1ECXVrqxqMoTNnvk5MHw5Ud0Ulg+2e2KrLNNFDPYSjLVRoPvFYZoQF3D73SMx2TvCEkFy6qMwbivulixUhGAgCAefqggHieyrONW2orBjLaFVFeHjBlDzm4VNBUDtKDMUQvqEGCac2UAKAqpJ9BwqEBhkSRB7QajFyP5rCIvVg9W6wa+t6ga/3lpEV18LBx7ZRx75Vcgv2uWKF3c0T233d/dintZbpw3GqfvBrNMnKxY0Qj9bEXraTujpIQl9RbzeuK1wQXip61ByiSlRkHIKyqQ4dKE/3XQo4Od2Qv/5kITeleDUJKGSgc2WWDcFIRZicHR2e8yGskJ6TVc0JMADBPTAXAh+QPWgbeHMbQcB2kQzp59NOYiAy9UQoiCNqJRCz+pBFEMYozGBRqls+WTfu/+L+/6rwcpvrYKV377u+Lfd8V+B/LKdCbs8JBO2bKt0c6Jp0a75rLsrwcsRBjk6ghjengs4HBO2w8bWasCStRN89iF3NCbHr73sMSJ7ilrscUsmlRJCI6HZxMwhpBTjSCtNkBLNMcyu3QVWmnMuMCNYsNXD24fGgNPtuxnDdgwYHjwDFN/OAMFDzLViRDDKNJeHLv+FYx6reWreTv75vuW/8/HvD0KOZRIwNkllV6zGjc17FXy3W+Nuj1QdvG042xQQjNqxYnRIAQHYeM6QADvfpK1NoQ8iYq4Z9YfLJfUipyq0dTstwBcwCT7hcER+WmTXgyLfIPKpVSDeRdDNxx5ep/CK+BL7J43v9S/sn+3NXdLpXbhg03u3JUh+mhMaTN/2UQzN2zWGBrENlGO8Dec2b36tHBSZYvghnevGZd09h4RgyZ6H1VhhwZkUvjqAdcgVZ5CFcf8LFx9cU2nPlWtQPUQR0/Kz9qy3HHY+UIF1NwRDG2KhQwqFdtKwQxPXsoLJSfayXsOIDKFBM8GkRsT+VupwJdY7SIl92enm6lmDV+aqxs15g2/fjov6xz+lWd9UtcmycT4IsG90Ay3Ku4YnO4vDfMrwsKqjsj61tc3A5QUq5ERxSjCIRCEuvWfjoWC2tk0FcYWjhd/N3o4UWUDqz/6HypcuJjEg8DK4eW/S2uTBU3t4yIFodgeQ7A7gnX5zu0d07e/OFAAplSvBNdgiTAFo4k+USME3gruAQ68oMhPN4sdiuR48t+6PxK7ZIQIp/ClqzjbDcztv6BYNI7sThH5uGsYhEgRlotrq2HRnCeykxEISl6HhdhrGFpD6W2qCS0g7QKPO4Ws07gdJaipTBadRGYFyZcWgjIbDh7tjyO6rZGsSjg+mZBACCEKk/f8NxSeb9PZXLhDTNef5ubyblr39vLTMn/XFSOymZkfzfxJhryd/J/Pg/1BLBwh6E0l77goAAIBGAABQSwECFAAUAAgACACabjI+tLJ2N4UgAADvJAAAKwAAAAAAAAAAAAAAAAAAAAAANWY5ZGY0NjY3MDNlMGZhN2VlYzhkZDIwZWE3NWI4MmRcU3RlaW4yLnBuZ1BLAQIUABQACAAIAJpuMj4npdPx8iEAADsmAAArAAAAAAAAAAAAAAAAAN4gAABhYTc5NTQ4NGU3ZjgwZDk5NzVjMWNlMzQ5YTYwYTY3NFxFaWNoZTIucG5nUEsBAhQAFAAIAAgAmm4yPl4onrZiFgAAABsAACsAAAAAAAAAAAAAAAAAKUMAAGIxNDJhYjBhYWZmZGQwYjU2YTNlNzViY2I3MzFhMGJiXGZldWVyMi5wbmdQSwECFAAUAAgACACabjI+ehNJe+4KAACARgAADAAAAAAAAAAAAAAAAADkWQAAZ2VvZ2VicmEueG1sUEsFBgAAAAAEAAQARQEAAAxlAAAAAA==" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "true" showToolBarHelp = "false" showAlgebraInput = "false" allowRescaling = "true" /> | <ggb_applet width="1071" height="660" version="3.2" ggbBase64="UEsDBBQACAAIAJpuMj4AAAAAAAAAAAAAAAArAAAANWY5ZGY0NjY3MDNlMGZhN2VlYzhkZDIwZWE3NWI4MmRcU3RlaW4yLnBuZ+2ZeTSba9/vo1Vq79JufTqoIVVCi1Ix1RRtqYQYSg1VY4tojBUzCe2u0gEhKma2mmMWc4hudmtqUJQmpqoxCCrm8dz2ec5Z66znfdd637Oev84691/3+q37vq/ruq/f9f19vtf1+p4RnPeXS7+AQCBePYSOKQh0DAwCceSd5AIiI09nfoJA4jV6OrfNAhms0c14J/NtracHGkVVOe3Ie5wcPPr3dN5/JySUywbdxsReVX2N6BYQlzTpeHXl2Jvg5vHNQrX7iV2spWFNzd1kK7sykjU5Pjg4OKxuOajbJ4NschxULuIxBQGBwk+Dbm2BQGdgINDE8b9v/8PIs+2X+MP95bC3DQe744eyO/KDbV83NdgVOz+D9kUm7frX9x9+zeQGSStjZdaHypZT18MO2JnnBFJQPDqg8j/NYEQ2Lcis2vFaq+Ex2mORWtvo5LX6pWY4Dgw6Cfbhu8Q++Rv7lyuTdz48zmwtxv8K6pLFRv0quo5So0V7FRKRuubQ82QslDTraJrwKOVM5btHTgi5X0HFBSvya59uLn+QX/spcf3+5539eBgMXe8ify72IzWPxzETt2HFXg47tN4COQRF4HnXU+CgJMunDzpde3Muc4Ja2oQC/vrMOFxh5md2T/sluRxfqIP88dHsLui79DnYjLd2aVhTz04gq21rj92T6pIRlEcPWW5K7ZJrbtxmZx42rjysSkTmWW0kDy30b/rM/gwDPhm5IooFXcbKbK5UfKMLrEtgWdVDykUWJVJDKtSf0ahdVq2XkTqrqvKUgifT8Vpo84ZBLHXcx876LcdRm+d3LYM3P2k4nbS0VxIdC5yMRuWn+7vWjGC6ZpYoy54xWgdbqIWSWk9lulP8TM2wp+BucNTwPhSP+kJtA69TDARjQQ5WkfjDLvLDK9Y6hztDzcpg3JoJe5HcI6vR4//qYu7yzMgB1UxTGfg4KlLY/+py81ofksYjmdaL3aSMe/CpTsXO2AMvtkwa3H9uRUq/nt3SVqXFDaJiEvCirZU/utWX3S3K7Eb3ttq0PPm09lZmgHQI9ZkvzFdebtocu3P1VcBYUH79/sZw6q9yjeX1c+/fplh71uduf39xWjciFlF+c7G8tdO0Sy7051sgo4AeelLZ6cuKkum+pslv5ZmfE70TXlnBqT1q405z5+1BDywmHHFmahGfsxDnfoSM79rxCMGFvHUKTfcONpvlzN8ouQ3KcL4If6m58S17u8M4tA+7YD3uqjyOZc+kju+hyMvUXWWvpnWLekYWCXYQCQ79ttjI7p5eKKMsNaxWcIsE/rG9Uds8uvedW+vJEjCAl8uCfZFf0otTwmrHwZVRUMM6gQtPdfcpBzDQSsKvYO0ZbM6luKdP+w1VlLya9zfuPLm58c0xlVUzXBp0sD3btcukfwPiKale1Pr6H2+kU/qNtZo448IJeK2DOhtW88ZCM3t/2J1syCOL11hF0H9WDtmFJGTgHWNUUVkTVcrPY0KadmBa6NdOxOmkLIqX7n6a/zQ3iGi49YCPN29zxMe48HGxdW3p9qzW4fbLWeJ07KJBB8HA6fXUzkKZl13gxMuZ0YDx613XmaeD9teHUneXm5ttTsO2HAqd9ibBhw8Ci629mqrX/G0wHRDaWznqN3cKq2a6InQtG5xw2fS4Tgs8p291JtWL2DPdsFBKOU/0X23kx6xqVJrXNp0LJPajXTQTAp6sc4LC8YP2kzwnC21yGrzHgmZxWUyF21PPjvNdVVAVCVmsWP0Z/rIZ0Av7LWG7EFZ1nzRhuSeBhJAS0tql9+gbI37XGTtYidSS2RelrxOmiTJMpzYkKmxKddqj8fBgl9YDqEflqXeueqUyQzk/CMvR5B4YJfy95uYIWfXnX2dT8zNDGzaVhBuioFXP/RB3c3eFQA70l/hgcqbfs6HHLXD/GiDjYTRUqsege8XH85AzTjwSXeJwkSAn8rAnRUmueQ+zzeCMx5ZuWOjUtOeNi9nH6yNK4WBclZmKSNjez5m6yRg32brvv/M/5hepLI6/wW8V2iGbyJkJ/LK68PTsGDVSY+YyzdSAqjyU7JJh5d+5t5avdZ1W7jZUahuYxlmwli/k23t7ehvFU0DNYwc2SXh0CPd9/hUkaDDtyKg/O9p8IPb8cpfs0UpLLalhkGyszuudRnjOhe0Oj59vge8oMPKrUUyxhDiZON/ciqqNSKHA78+nf/Lr8ksxokt5VJmQju4UGdpUyBUO8YQ4G8piJTIohp6SaqtgrPFTZzulweAsj5zKWKBjUJr/H4LV+wFP7NsLlgX6GqWwoPIrrW2mGXzWYHVNIeY24uwTokHlAuSRKBJS+HhgxXvlT+7EVCwOxnOaXkL4NCBTOKU/Dj9meEz791stSKJ/pS8GSPREV+QxA1tUh8WYmQL/Lf4bG+Nhh5XvCJv9FwjSPdOWzTvmzH3EOXGkFo6sQ/JWR6EEyDDP9m85tqqg8tvmMJRmRbXXeTjvMfSiwXH0sbt3EB7Khq/alUfCYzd4tbpkmNvf/IZsuxLm7+4oGalOv+trjosY4EwxgBoqiePHYV+V9y/x3KAsU0O2k7cP9tTNCZyZNkEwgWcbndJliol2wcwWnwLkLb8ilqLoY8ZYrDeH4wgICnrw24TjNfjr07xSp7X2nhZic1TEYNtT8TP1sxmC9dh+c60M1Fcz+b63cRlxa0QnK0nebKa8nhbiEqJfxdRrsHmf5dXFj2wxLg1PNDPpEyQ4Jwt61mV95hOoPtUXcHmszjnJ5HaJ8NOIbr6Kr+efldlMO/adXDExxy89cqP/norO96Pnjn2ONONiqBymTRJcdfPe54kq3Z4kFZVKgXscD6flwrb7oPpOaInMroTctKIyasMpDSS+PStS5KF/76n0ZfmFmuFGEb8PKWRb0JZ+BN6qCDzpWVn4ZI9pHPZw7s8C+4Bx3GbCSlxorOfcRctrcxGvwpPS7FJr4+3eipq/CH8uM10VYhwh4q/iS2EV2EqT0xqBfLTZmgtJy4osv0u82+fzhZebTk3xqAN+XI5HPg4pGEe6G3yz0qkfl2Yybi99g2UXQ51ON+lBm95FEUFQ5LRO6zVQlxpWBoVqq5rI1T+L9k90KrD0J+X0iGm39v0jBZ2TPGFS+8WooTDgxZ19VavHenUdhK5eW4nJlpacs54UDhQRUqi3bKxQfgqAjAntLQA3tpovlWV4lDLbEGHwGa8poYS0VsIjW4HcjJLq9SgimivpK94Z6f6p2CUR6TGS5n+GUUeNdpXP/2Y0XK7GKhX4n7NsTPEYr/K5YV1Tiaqz5MLZBk0nQLBOf1jCiKyK/rG6YZXRRVRHbLn9wWrir/2IyAj80sJAwAvjhDwjg/SqIue+v/r0yCYo5iYAQd8uS4PjPZ/F/26QkBrY7dvxuuq05lpve/kNV+b7ZZdcV4Jz4inu1KqpL3y6Vgd6FzsJ90rVBKp3saVNGwyopHgPrt0R/8tx7dT7+dujLH8OB6sIfJDZzRlzSLLv/Yy8971DyzcMM/+KUV96kJeDkgkpTft9OF2VIJ0lPvvJ6fuD9C55WR2dOwalMtfT/Qat7G++8hyp7CoI/cfEcSDFtpKGtmVx2m3nfc535lhdzo4I3p9Rab7W+lfliS26S+Z1S6Mew9P6pMtgQNNaHCHYqZxhKtmuodlSRN08XYiY6JbqUXMNiUz+kaLgOr+sUYh3ZLAaQOXFLW07N3ucC1s6e8mmecCoTog9+lFSO7bT55aQ981AHwdgzAU7imLlYCjBuwdSSZbkyMu4/be0AsocnOxFSNccXZH3vUfP6cgHlT9ubVO0b34nOdGNiR3tffquMJeHU7W4dH9X91PxbCxl8Y9CcJdRChtAC2T2BKU5LEeN8AbeYlia9i5VwcmU96iOUs1ep1TRAuaWT/4toYjqR7jlnOQNl3XzsyKAMs7EavNd87lN2jBs3Mfx/Fb4yuAXPqU0JzfvFLRPbqI497AzE5K/7X+olZcuD50POPaMVwIrUzudFKRZZqbF/8u8KYL3/GjGOzOo6fYWUCa3XpYxi4IHOJ54bFOFjBKPLzAOL2j7n44WZMoC8vmjpc10wzVqYThpyCfZ96ArdtavhUfy3bZYsjahiOuV2rCYYQGan6Y8HB4rWuYTsjNfkH4zPkXfhbkPenbOejtJ+eRAm1eXRtSQfVhTEABOnQmhke5KTVs/3iKX/5pOtLdDudgEjPrRzhprfDmqhi8ylmXO3tr13GO1AWVJvfPBhg192/Q4ApZI+uicaGuR4VOq0H0zWzFDJGDEm9bgt9DpQOZMWkzraPNx9bIcFw3EgZcFhbV8mXcBDL4bif/4mdU+0FftNqQMTOP4nUzt0iN8oWO6rncNu2vSmtn+AGLK2ifOa3t+F+AfLL0RVXTMtyeASTGZdcO4eh4zapoISFXU2l0kz0zFG8taZoQI99hpm90xlbpcGDVQUoPWpwUp5mcEu9IzUm8QRAg7jZhQGhgo95jqTJd9m0sP28xlGjicEEoA1zgDGVxesfSsbOQ7WdjvK8kccu+ock+fqV+82pHAzC68oQEodG5DrEf+dgZW49wLd/ioO5nW2VsGsBolbR9KunOv6Li2xHsUxd0/dcolmqSsc0nHB8KpufX9xa9a6qJif155nhMaNoJl06a9739RPaLP5djrNX4M17y8PGNxy5r1weX9uWx8Z3mlGXL+EHnH8JielLYAwqL2MEaNsyftNEj5W2dbTv2l9bymNpGQv0FVtQyiMoQOC7X2HCgUdyqal0h1N/V/M5AbqzebvWau/eNgd1luIk/2bRTFRPKqcwtTfbnx/pixg9pMkuN50tW4UXkBNSK6gMdqNiPEk84Tn5ttpl9pFn8mHpJrw3LVtcvkJChmLlF3l2iylEVTImb14OUFuwd3EKF2JKkgvskahU1z779n0jvMYyg12PND/XOUne7+r2HEbfAo5NXnj+18cad2GY/fXu/cXeeCLZ16R4UkmWn1uREuxwseVLSJWHtuFD7VAGgyVxJyLsmG51obOAzLtHzt062ab/aUUTbJDcbeu/Nx/mtRF8GU63Xu4/jpbEDNilTXerW72jfMtDC5+oTrNdtjBoa0Nv6HqzarQpWL8SS9jDalIZv7xEAor1KTxHqAyHrIJqub45nzbzBXcwcRyoMrYaNDgp5ECDTWzdTv8dxeLKJMR0rEarDdUE00X9Ml25Z5cTMwM+wgqB7Dbt5doiCdJ1+JxVzFJzvHh6eG5yvGzHRq4NdKBlqnV5exBzSVcZstYbFHRco0iQ/iryA3c65gmLmJyoBRQwXt2TC99L53+Bj2tq8OAEBrh3rme4hfVc8Di+PjrhWuyyR7a8q2cP9vw/Y5m16l+SdZ+XVeT/bwZVW87mA7NnpkyquBmYcCYP+66GXKI4bKAhrlkINWFJ0ClqlskxDd9n7toV3Y/vp08BH8xxB3cFZ8HTFEmZKcC1Pv7htd0xSRzAh8jL5kKOaW4si2YasNfBpQo2paEh0wEF+nDkjWFcpzRpkVi95OMDpmGKzlz0Dnz8TBRbbvBAqpHB4HEW2B9VHDWJxBeGl7UqvlfQZFH00eCNM9CFJ3aubyNsVUljZulXuecDK9iOZONINicKsdkvZ1zwOO36ZKiEonxJgp82v0cRO+xz0FKoqoJbVGOS8vmLAwEQn29ATsy+p+4RPx4qntzRNvGg+3JvEqgO5YFrZMzda0wgPy8SU1IPfyiWwc2+h7+63SDZ4SNoM6TP0t/83Kj7dyxHQwutfgpB6oo1KvdFEGreLIp/pbgOnLP8owfZsPY4Kbm3QAXCPtj1SKSVp7Ah7keyXb2ay8EmAjXih2zZyvLz4243Wj8Po37WCtT+lW/PS+BhQtpc+aYCtJP0EgtVpYe5iXMhS+lIismZs2iDr33WR7N8N3A0SgL33n3PphPhJIQx4bnqDCAl/7WW9zYdAD7wnHvui1I7NL1nQ9/FgsxmjDGdY05MGv8GYxyQiwbgs8JqdsQsz64TBSIr47RgBaiZ173fRW8wVqZDLvR3xusrtc96oFSQtXRl7h+MBlvn3RfLDHM/pUR+fnKOrkxIX+hS8HqjxC9ruMoc7VTgDRHsKI6XLM7QL1+1A9JR8oQ2Vi0b2DRlnCCFjuJ818p6wH9XllOHoE06IIjTPaJElQ+fvWtgJU/8i3+3FJEGzUw8G53Ya96cyOzEL/HLRC15mQpXoXgcUE2CsbVUEJUYhhBvMQ4GiV+UZa392xGZ+gbhaqT69JFOkHGi+O3IgOiVZKO1Z+paXt8UEDXjFUAjsQ/yS/voOPWfREJQi19PELHGz7O9w/aeRpK+90bJ0NM7L9IpsTHx7DGW2mbqpa4OUDwQ64tptaKA0GJOhMH3927gIsb/+tFtRdmq0co7Ha/vK2TXwNLWY+e85to1hdHaogRtbhvwEtkCYrVS4S9OHpHXHziBST+9NPtCx4wduBulUuNbq7s0PXa94yjQV2NJFNUWJAzXRvbatS+dOk6SKdK2UlTgBsNViA18z54tMnFPMwF9GszWfV5VDqrkKr6T81pr8+CVh0aR9djLOehPodBlmXQVZYZfdlVn7RFcQxVb9KdeiTwh8AKPXRAoYaLfmtrGnjYaHukS3mfIkmejdM/LFbAyzkIbF9oQs2T2/Tf8ZJIfkedg30AIYo+9RCZwKLilajXd3w/OBqaeqam62eJp0QF2QmhxKWbE4KjaXO84NkulbkkSdymhIUht3vxxXMFhuEvFhUd8xr0oZAVRVvi+0L81y0Ug76/pw7BaCekkX/Dr3Kej6NlQ+YUoO8SN2AGHgAt96uyxS7cKT4L/22uvgIoLeReP/jT2pwqGQxpIDVJQGlq+4DfETql+88nNVSJvm/5xHiMuPZZn2bcVJdt7mFB9yBBUrj4Ba6RxKth+3MZfObQVcbud6YtNbO724HsbKccP0mlg+3bswef+YsDMtDh7uPD/CfOdpdMl3fGl0OrV1Jyv6UZNyAHtTX8S+sSrQ1jW5/7qX6UfnF5/lCsuo55WEPnxj97pCOhN64LEfVlRLBiAiz465sZg6qLyg8nnoYGdRzDlBvAFl8lRHjmK6vlva2XCHOydlNFKf2R564+7CFwW/+H8UkO1HJEKQ0jwidThiLASo/KTxG6BNxNq48Tpqtu3rzaPvL2iubkqOgVxJuQFZ3QTiyNGZDo0KEX54GWehsJc1wXbJitBMHZYIG0NnZfOpucui1dduqWa8qrQzpiccsRrVzJPJTkSV9LLXfYROwmvwG87EVR3ssZregrpqZZT1uI1lPyWZv8jQPUfLWHm0vwQnAl822LppHJ/laIKT4VO3F1W0wAyG7XOMXNHRxpbIVA6wSXOay/kW9gvbLFWZqlZ8JIrFrYVP656YaFkrd/Ic9ajF7WGFtGH5FXvbVKdu85KE0fNajk/+0Kd+LBGES6Y5QkstkZZesm/+3R5GrNZqJjgNGif5biF7E5YJ94WyJIonAxr3VLppwwIjJMbg/pdiKnLdI0rOHEy0xzmPwO4j0pymz724RKhaASbu/PZbL4IAitx6MXwDJUFbkl2QSqDMfT/2jy1BTZW/NIWo4RU0qcMDHXIK2197DCFluQmajud78bW0McvLFDo2mIffNMwEBgaI0LaVE6CwMUAxUgPT08OnR3MRmdSosC67WvVghYhobMoDf47R1EWpLbmKLU+DQ9oVe7dPXZ4urvKijvyB25fnVGmaL12hfC+LhC7MLPSWlDfMkTKBtzRD1aLsQwAWbjH4AUKxhGdLabfwPTE90nIp1P1GqFYYz2LcZd6k9CQYV1wFDQI2UGOSkxFoJCsx8PcCOWzA26mW0jxlRZR+933hS5ZWmmg/xgRmpMXNmOiQzZVzqptZGwuOA2fhr9ZsjPkEaJ5KsvrrWb5w4epOeMlxSKVP9kc/L+jPUsPb9CVCXFNZX+tdJWGbrJOZ+DwZJ1GRMOA+YwxONU9gm8MLaRC+M2pL2aU2z4Jt9s3Fj+PB4gxuGcogdLVN6exaG7p8KIkgfbzfdbu8lc+auRU6FEF3pzkDOBF9ZaeSO4gGDZBZW5HWIKpjcPxUpemO4zVG5zxNP5DKrUu/u3mkrOOu2O/NsyrEQg135k3s6yCkqJDTUvz4N+P+5lwizCbYqPILrDvWf9xCXO/iS0gJTvxOkECFMlwFVObYNMRkV0Zlz+xHxyMm/xAtdSpSmpdI/PQwoWBu96nbCcQRqICxlkWoMvz465R2jNl/Arwy9rdQljZallSZqfLINGP16tI1JexQpbOHf5PTtQenXIkuVC7a+JlZ5HZszbB755A8MTfnaZbNRbDHu24jGi/a6DxVmLo2gD29+ARdinOB6pSMD9kDqyLEc0JZ8DPjA0PQ7qgDYrxZpO8gMNcQdAsh5dbZW3DenQxEpT+fw2WHmJ47K0b8SDuIVUyQKpvTvdbJpMrFYWugua0gDkCdn5Y6C10Wj47m7jYlS4U9unri1NVegrouxDWFVQ2wGUp+EdORm3Bke6vlSK3N/Flv1Qn/35/zwDpkU7GBjVIWbjFbpvFHRmCl83Y8O6dKOFMIgkg/jbG8UYjXYnxUgCMOHXK7LdUyLp8QWU88KP9J1kDQU6xSgd+mmz3REZm6MYuqgsAyLLjwqgqfeMElUxOh7lHrvg4NS76PZfoAwkZ0qhyW4aZBAYKmcwwOAWy5T4cQjMaQ6m9Z/VB0hsTkXxDXBTN6g5aZNalVJrTVHYddtHnBm6A7ayxgROpT7C5jMSTB5lCM4AsB3OP5v03TE2Al/Pk7+GYe39aEpTbNxChqfoh/0DA2Q4CXYtRPPEWfqAWOLjEV8FDNPwh62ntYaWQQUw/lC11s56oMUpE+lZwnWCT2z0npabkIssitXVYlGqmdMZHNFb+yyZntLsb5FGjjH8dlzsBncMdmjI4+4D3EsUn2fVlw2ixwVl9czsmYqelHpTVOZnPih0d2ssa22l0SSxRXTekCH8HCut7kpcboD4Vmc8YuhHX4/XksSdfvNNCxKHpq36MMy0MXVmdl2o7aqLMgfG+Vkz5PJlgrzivEm61jQSsJJMF3JNATWt5Yc0S/zQsezmyW4Vse2YagsNej0155TMc1qb4zZKwZIvcxMc5V8n9ku6r+NRQWKn8qtFSPf4peNufnjFQZyYzRwMhoSKPT0AwfkqjMfgviWMfFeNrfKJaqqVXecvRBK02hp62VVT36q/hUMcr8xkX09Os2K6/XIQKVfNcUXyrxX/9AEsS42VCAS1Wj4RwFvaRwMb2YHZWhSLK+w1aGz2crEmYZponXnmcqS2rGGxXd6H8WXXW5Z1ebnyLkPzCMCPoeE0HOXI7TeWpGEcfmnjlqJnRCrfCE+bH9WCKNQ1nUah5Ssjnw/am0y7hWJ9wQV4pMhCe543PpXy65XazK5OZ1xZR2B64u+HWcqJvFa1LVAp7oHpVEPAJhMICiW5O18CeWbJClkp5gMNx9ZbvLI4qx8j+PIpMy6qjLoJHiBdkRi/hnioJzN98J3GCqzI1tuH7NkvaZIE9kWRg2tbVdoJTwX6BUEQDfO8QjXjgW7+RztxG4LCwT7H224liHPupeaGXTfnIzq242rmKdfiwcpoFesxtlJirKhFV8jchmoolUAWi/AHh/t6uDOobcMtHRrGiXu6TQVzs5kisQ1hH8ZM7WuHZkJmTds1sTK4ER4zjL3X53W2iuXKVsEyh4twdLO6tjHExds7rXo1UzMsOsx5w0yrHc0MGza4IjaZLaXOJby+5eMxpTaUcEgnGd8Xrys3/Tfu3ZnYOGnQeH4ddHbDmyaipxlsAwmDVfThILrD+hl+SXnAmM+3jmP0VW/6ISGIGWS2XGQd4pECfeRsMN95wufGdVuyNOdgKe3FlH38nG+/NC/UecYAvV8wMdW9yXesx9NAefaBS2N3oLO54xlRaSxoPj7nhwOL3jAHnRe8s9Pgiqpng1o5p/tdKnRUTG/SrQw1GL3liuocDiAHdqN0RND76hAr8pEtuXSlSYkHolbP1WgiOEuF2LFnw7UizPvdgwyzAwZWvma49kRrx/+fMIdvyFD2BjCp3TJI4GKUD5SFx8YGX4O9M2hFW5N1DTl7bhXLoOvOuzrMdRIeGXjR8/FvSgb9mZXYA1LDJza9GeCnYqD78A1f9sE3Ny1PyV5SfUYLsMUG7eVOT7uIqS6UtSU23xPyaNs21y0pX5E9+jFS7DzIY9LOgFHCod/Ss2XFL8t/qLTtASxfoWsMm8lzUr1PnabJMQtEuhAN4knWwMVraQmYMQbvp0SnswZxRkXnmamJls/RVj9aZPMTViRd13bLXjTUhca6307e/lGk6juS4GzRhxnYDOXJxzjDZWvPZr64wWfVNvYbCfn1zXfgd5YD0rteGgIGbBg0PS1YnK3VOQn54JvbmVNFsEafS6ENr25dhu8YhJK3YMlXXg7Tw6xNjpHsfaC2/ZzvrRqaTP1oJx4Vua09QSp/QQAVv4rfZKVkzHqxNYflVgCNVoxccZDIsXz6LTJgWKmaqqp91GsSzVgHBeQzDTZVZI48dY74Y2JqNPgrRt/7XxjXjny5HthRZZlnkfvYHJJcVJwGHH0umoZhEay8u9wqHCfoBGH/RYGAXr1IKNvsMb+okw4IubmdkdyeuWZ2AS0f4OMxNTJowNm5B8USG03B3MYql5KkpdS9NUahF32mqv89Pgz46kaa9AGdAbGRbJ2GlYZ2dgY+uhpwop5APZzGKk7Uz4w4Wij9WaF49mKvAuLLoTjbqnOj+ajExiWokwuvGjboHH/kHx3r5SuPXlBEakE9NrASmDOSNQjzH1k4AtV0Hs3fHQDsZ5l/jJorDef58xbJi8HaMKxc0W+NFh+KZy+tLX2cOJJmHFJWtT8+hwXIehlDNr/q++uRYSB1TkY0K+Zp/FLlIkNXk638agF8X6rIi72HOsiPymPB6wdmc5zNLy3J8E4S/vmtseJ0jPmE+03qtC/t1V9PaX9CXh960dYu+4B8u/T/P/zYP9fI//p4f//evxfI/98/L8S+e83+2/pyH/a7L9l/BOtSBAwA6BnKxzA1INALdx/3/6HkaPb/zjyz8f/K5F/fuBfI/8Xzf43OvKfNvtv6cj/H///Q+P/gDg8/TUUqu2t/9sQCLj07hrplN5x+P1/AFBLBwi0snY3hSAAAO8kAABQSwMEFAAIAAgAmm4yPgAAAAAAAAAAAAAAACsAAABhYTc5NTQ4NGU3ZjgwZDk5NzVjMWNlMzQ5YTYwYTY3NFxFaWNoZTIucG5n7XpnVFPrm2+wo6BHUAEFUWkWQEwoB5CgqICEooBwIhBESJCSIC0IBLBw5KhIDGCA0FSa1CiB0AQUlB5Cj0kIiNQQILTQwdlx/jNfZu5ac9e9Hyef9nrXXs/bnudXnp1nNyxNxPce3QsCgcSvm161BoG2yYNAItl7dgEj/ffH5kAg5W3Xr162fcCa5kRRbvUyd//g8/3Bz67HX814KFF1V6rzn9NL+++S75hcU31zt34gY9fB0G9Pn3/XUmYObvS11VB004rpBuM/E/hQehuptXo5Poz+JyWiSFAUtGm1E/RBbhOPB4G+zwwNG/5apX+e40f8qooOr/VZ0HuSpt/CKwnDNzuuu5Hz2Qus8LF6MdBKxGHorp34mz5bNnOftCOubIaR0/HDkPfpC+SIzfxol60Gl4EDoK1z9Y0ffpkMYBvuJCbfGx/m8RsPh5PI3Tz+9HJ4XDUxPWKrIjp3rwNo1ll/4cJr2Akbg/UL93a5psCu1O/Ky93YmPcHrZD3yj/BFNSrWgU4YKQDJGnRn217QhYrZ3Lz9iVNzrqMbX/4KwgiT1OKwVx2DT30ZP8xaWpjW9sbL5ml28npo+VQeyCEuPwmJhGNutBw60CXz2oObRlNxDfodl+4NVQw7bXtcwRy5d5W6FmeDqvvdU8tL4fd1V7uflhZX/LCxKbI57ZGaU+Fho8bHfBLqyNxVnZ0g2XHUt/hhsnCsoE8KDAE9qzeRnPDtkRnjJuw7+8EdWvjFisv+/A56rSOj3e/PZ/88eRA0RLTPX1yc3mQPBA8nupZ/1S813BrDi9hDI6Brk149hXAeyd78/MLHcqWUtD3jmbZm5T90GR+uBu1F4SCUq+I178ZkBGU9gcNhvWGr0/bqzlQC9aAsCGIjQOGGzdQV1HtKfDHLZWBvPDORoWarTXeZKN8RP9YxXDenPQoZNtDD4OFC+am0qO/lkI5kQuCF+dr3hNV4da0VP0yVomHDf3FzKfg2rmGY73A6uynK8bT2G1nPy2xvHoDGU72cvc/i/R+bDzu4OT77XAvEZg8+GUlwi1Rj+Bb6robNOQqsQlp+MhWenRikJ5uWEvS8UHAEatb63zYy8YFuqGz0ddknxo4euDTqhREmnZpfrn2V1hy+nTtry2lB/0B3Ra9ownOCIShof5CGyTiY+GDvOe2vTjQJfzsBWbhx+G/QprAMKMv1csDDpywZU5W2jAQ8zytkSRhWrMx32odQCIgiY3HQwvacBuL3VajFxpl/c2TdjKBd2F3mostjiffJkQmqnaPzAVyTP2PuIXqHNz+0OMY9Cn61gBv6vVlmFoqPj8LpUA5KLpzELdAO4/SDOEUSFpKGB8PW+yUuAOG+H09aBIfQmBjqqal8PT1mvWZql5Jq4s3N1fpEeoKghO0ZW7KThns0xyHuBLEW3FQ9mZbo+3S1/fO+tfeyYgenaNHbPl3tRqkfssSlRc9Sb+4YF66PBC6zJm/HTqZm2PGaaw/YOhYvdgFq91zyoZ5XwwUib9w/GsfD5U8io9m+9RW86Ya3PbHvGi74/hg6O9eVqlXvpXhZklPSEnFnHuSCiMOmWxjqYtMjnPPmX9lMATsTg5KZTy6Vxc1KwIqdIc2BOZ5Ea+B1aumignYloCneNWkTEajXFD/zb02NuudqDMjGXgoaY8qsC/+1yODLlTpc3/ufHg9Eu8rX9cH/4eUHIqlZH7QHJ7MJ2M4VhkUasbCci7zr8oAj9IHcz+7pjX1kV3nMml9Px6MvrZvEWu6JuVki1Ag67RfGY88AJqQhCr716MlocVK2q3HmHuTCT87fDlfJY8UV2uLfytOVgozWvruineeUuX23tLSR81U8orACv4dl3e/VkrJJe2UgIL+gOZ5jhSlocODgOKLR93Ntys8mwERi+7qu3j8wY9HEifmw9r/ZnqRq9fUyzTrTSYNMNWCvuIFJXaA4dbKcBGtsaGTdmsFdGnlfR6BylxKPnivz83NC02loOzeUsqMk990kr/AM9sVBMd860RVbKOOh9yjp8lxjD6nBg3A95NhK6b2vSFcZPHuTlF5UMcpXPRtfud5HG6ZE6R0qOfp9PiF9ye0re0lomT9mq6u3OumKKSFLTEngVst2G+4Mes52vJaQQD1WJcFJVKHXPOOvujV+d5j6xg6XZp1OiAx6/nl3f2BfWE9gYoejtpTX7D86mWEADhru5xU7O1S3Or8o1JVTyjoztckfK5ereKwgOF8Pqdl7EdZc4oYe/pHGabKrnix61PuAUko2CuWcse6nCR3Hq2fHxNSJA7aIx/WrpNkfmwRFzb3Tap1f4IQYlR/ymq2XjiNK9F9ksXgD1Po0PyalZ8vPJnFyN7rKqk9An6itwv3zRE+6AQuurygA/6CEOfGc53KCVn3JDqzlsS4F4eVtORhRNVc9fIfj/NWK6J5rMrpLpGHHjJQYyc/GU3/2Aweo9DBvjSY7Kutxyvzz8aucXPs16coVrpD2q1qVTOVXoE/Hu0mMvEhy+a1s2Azl7PAWl0TuRPafpGbawJevu8nRjnqRBdN03Wo7u9ecZ3+G1ubK8P4hK0THk+J/nfH2pJsjiaUnnl+GDiavfUmtawoTOvRitzazSX26OATlKhxYf49SQmw3xLMmCOvWDgopXbbFsh5XyRXGVMxSuxazliVeenFQ/sv7RQWnHwaccxJ1wfZESpOKcV+R1fSGP84WjUI4fVxY7eVoRPR0fo+69OSrGaCkx7hRldh9tcvfiANo5XEvIxhf0yLGwre4PQjSYOAfLMjJlrLqy/+ykSXoyq6T7igrkda7l/dGsY6TeRTVz4IwXrSfk0LKgks/Z/ZC4e/ZNQ0Z0c0fBhy/c7R4FAbtH+lXpoD4J24FlcSQi8fiYW1nAzg3r/t7FwYHk4dashKQNyeruLXsDcsV0APD7pDsz1lsd9dRmeprPf6nsoU2/jKuLVBUTkZKWfcnDajB12h3KquW64OloyVISAiTJKV3rS/2g6qa3z1smpt0zkMG5MZc3dpitlrqT9ti1mSqXhbJn5oc3/8MdtF1rk9sgD8I3so0k8eW1aW9AWeC52pcOc6xXZ+eoowMF4TXBIBDV1Z+QPYSmgkvpmqyj980e/5NMBmsJdXSViOP91g9H7FjlfRAYfkDuGU2Y4FFvyX3mTaPYdkwqmekmd4TWX95X7/1veDCl8UdrNyV39v6GmhR5P4n3JX/F85Tipau88BkG/V780XQoN67ca8H9FsYZO9BMq1QBK8y958wE6zuqQUozqQUeYNrngDbS5VmLpiH9mZDH5x/ujzc0WnryUBwNumffmtjAYCQNFixW6f3Hfs0BEewGct//imH+j20R6nsjHnICcqxmysDEqjgbIInXjYJ/MOdIf1FE8VyXC4k+ulUZyPBNgb+ewU5UT1fpv1uUZ52KXmKRN/7t0bfzSptmgxHG2Mqe3Yfdqpb90cIfLLgxERAoDfiBGDAHEjM2GeZcteNirbAVq/rS4T8DR2TNxQ/JMElGTIC4wOC8F8AphBUuRdeHp4oGyuEhzAWBkBkaG9u7pUXKEaim8CW6Ogp7RUZQCMmtAeck3s+H2NcleSddba3BzDBL29CviLYN/t/KAr7XQ/iBXtq84gziZtcPUThr85luxDhNiDAeYvtuDHNM+wPCje1rtjQirG8/KLziqk3oxaFfv7AFANeUcrjpySu4S/ON80uTqezg9RmNGS7LSl4xb37YH7BfMKy5RRcsVeYw3HfGRh+5Yuy8Fcvz0/DJy+I5aJRKYEdF2PwxB3CVc2pNC1fvfL452js+WL1dKlHyiDwxKWftqtnKBBpwaAkcC+f/S/1zq+SfSafBO/v5Bcs+aZlKU7lujaYtoqcMHy9sgDsKBWZ0I+Nq+SjrMOQSjiRrL7sWyuGx3b3Gby3JznD0e1Jc69SMK7GFmwF+5OzvrWi+vEG7F2FNZuCchIt6RmpjpIY+dQBmTPV+C2nI2NTB+boHZkzwewonUGHriewk0BaYU841ZMa37qdOp6x+ps/QEVUg7Srdnjxsc8gEKB6cvqulDT34TERk3N/kGBBqDPGpmM09aG8YZFM58W2sHFU34A+W39rN4diKTNW9gky8SZTqxwc9LzgJ1W36agLGQyNjhAUi7mht0bUKW0uv7aXD7PdusW+PP6Cm0GPEr2iycFvw+q6hnKQD/yomBHouTDT2fM1LCUcW7PlPT9lwZC+c+WptB1DrUagMbUwy2yjrKZh861iutKq8sZUkbAkwWNGqVSuj8KMZ01gB6Kx+ShYz7yvWduSUWrO9d86p2HuWUPCyVou+GvDYk7LFlFFRzo88MkPGIYkDTnHDwgXdoGO7PR+/29Qs9i2EmPNWWqhmP0WwCE39ciA65G+ZC+nIRdfSF1Xr3aVILUxTLICMeQZ60NDf8u0pU+fy2bs43tFpIFejjbOZ7tLG8oDw9/75BjhVr3TG5cCkF4qk8uTeqmYDrfXRsl6V0x908wm7SeL9fcAXPx3na1eqqLF5waEbGNgQidvoVdjvay2w0k4nGdth0vazenfbKgpxScjJN1NppntGW0cZpln1BuzYowFRrzxdh7si8Asudon9Nw881+S20no2TBtndavGEhuLY0g6qQ6VIGoEOk7VcmSnfEjr7EWVRfMU4++sIl4QRLcyLvSUezSrqjcfvTXLpdblWGtjM/GtJ++rIC7KqouBTigYtuoE4Us5TJtImgYdKSIO7E5aJBr/hwpbrdQH4/BF0Imumf/2GPCM6KxlCU6tPSrelmYnvlUy+f0NlSDXO7uDaR0buxuqCCyA/WcFJMzNTQTrW3eUMaJWL0bUOcrmxu+jbK2deZyF2clAMP/3lGCpSNXJmw/4NEPmdfpOrsL0m/J/kXK21fN5qaNTgMSOZ1vxjzBoAfW/3Mxs2vEq+DIbFeFiumCiVT0c1nyp9Qh7H640owS6blxZkBJSDf9sgDC90gDWUcZ3IJjT2t6hl9QT2D408RtRG1ncGvnI6mIC8Kemx6Y5VgZsPkMT+Yp601j/CDEIKf6mkertQ6lL8eqOllrFdWn43I3O8Yt8kGEEL6FM4tCMaxM1BwsE+myMfpflYzhEV1AXKpwjsCvetJOBtlX3j7FpbsNhIMAJqPABDmVpGJU2bNRcSXx3Ts6NB1bxnmwTiZOOp4dY8CO+R8xUisXQTPbe99kTusKDxCpy3lJ+sTfGwMQdeO9jPtRyY42aGUJC61Gyz3P2Pw7Rbhv1T17azdSASZZwnO4RUBuoXbjUJ83UwsjUyMmoWmxWDuq6SBc5nu9q4KC51WC/2Z8uH40ujdQuW/i6MoqU0azCH+BCzc0e9JJQwG6terBERILgnibilIHtzIrgQOukz0RKrCo/F/FGJOj1e4ZZaG6uGzsxXE6+dJrUS1c5BTcEzz/gQ4BfV62QMi2c0028JHbLgGAkYP33/JAuDlk/UmRDBpcDw7/VKXbnLHWEN/YYwCre6IuuNfKJniv6n+8JwB4yqX+qfF/bHL7d+LkTA4ohkOSdZGn6U3H1wOdizyBYAzaynDH5uTxpwY77GxKiSqO7H8n+ZYrEgvhv5Wkx2/qhlhUJLOTM+9kQfr7a86sMpv/J8p5PSOdZQDRJ3DQpdx8oIXxm6VDYaHih6k1f8ofqFEUZIJ/MPskUd4Qt13QCJ8FFpJM5DQMbUWm5ct03numQfh+5/rj8bbmN24ftKL+NhPDf04CSkFkj6JW9y7X1cySwY6+fkVRzkp7N7C0eptpk5eBLJuiXqgrEdqmiuPIhv3w6bWue7qXksIm3Az6k0PNrNPAXICjrn+yBtx7tu7M0enj0RL6IGLoyGuDdHFSJ3AU8GI/WnHtB6cBpwHFNiWBXjzwuQxP0ikW99JNlyoofoKW5IzZo7c/qXOvicJEnI4eJ2AxO8gPJh4G9UydRWlOSnpkRxFGw1iGsQhE3oyRw4NkGu3Knlt5saeduD58gANYU60tjUL7VbR22ks8yZVdrsQrX51+LuSrR6jty5Ot0heIr3NZBebsbMRomKiIiop943gW02ragBKn6NIiirB7ZqnTI0XBN2eBtPdkijrA37tuuOLn7LHtAB0zU7GnIWowFtWAfn+9Cxp+haji+d/+LeByROIFgiSzjKcI8KSsu6ZlXXSknV+vXsPOeky9/Nb2HaTMkk0xQALgCNyl6K+ZYzB0nfPKDns6Sr7SRJ+TIBaUmIIADYhKsUfyqbC9+aRIZDjtO4Q/fp6DZXFvH8XTXpPrqhBJM6AaNFXMCsAjqLhx5uXGJExPc/7AVvf+/zwOTNf99vvcvI9ytqzOZifcMvc7ZeJNn5H0WU3OmS9GEVqKoy+0uPox0ZCFdILqEy9g3m70AozjlDAhN0xB66l+JpNu20z5rV3qoXvvcnT1hEEjorAd3ETUcZ+f8WMfWztpolcqYUznure5sZU5lizdzy7zOjGMg6AzNmzF8xEkGXHPIhwiW3FAbHvegJkaW1GlBf3atNknkyeXeP0Q/ZB2rwtw6a5yFgnSJxBPgp8cieoDRftou8xsoPZ49yzu7iX5V0xfaufSdYK8c+0MiEvTwZW+/bB3V+/0my7Xq2Xsu0zdr98tXHMG3pM3JQsN+gJxsHmprNrclJkT6jYgs61ysTjAR2X2T3PApIPHmX4vZgVeTh7oeEHYVtnCtmafioa7H/jV5G9uMn48KnxioAaTO1ybnrcLiSN/o5dAGNnEakiO4RuwVvJYOXHE1iqSTLzOab0OAczUE36O7CKoLP+anGfRGlKSBWvqMoOkF4LmajzxlzsXoArpI1Rf+yi2ZaoaRZGENOObxZRFt6UB1yW03xxE3Zs+VBjtmFTOdEGYKrvMUMZ0Mc1DNWGNx860bIRG3MG61g33OpoQpZJIyDvrJ0Ce285PTEZL3XEzX1DpgB1zu55Hb3QUU79VvSfkO98QF7AGzlRToUdQQN12HV387U9glvhGNc3GTQYFvTbfam/zx1uApudFwXDj+e9MI9ivoS0v9omXGu7WvPLCEcHG94gPQmSwyr3daU3hq0MRWVd/95f4d8qH/jdJeq1Zb7oqTOXCtf/2QCMGVLKcn9dq0igTD3CufYDeGpcqP+kG3rtnQ1yR1+H4y26i4VIPe7vDKjUSUA5qkJkBLEtADe2el+3rKMx3NPDqIeKoEIyAlaqOydSwpXruug1FgtT73QTAzUchDaUVmta1FSmMsCn7y/ukxcaEd3QLAbPTXv48T7198Ie23yiav3IpaqSoEEAT2WEWDqk8Hbk4fb9iT3R16gbM6UMBHtHrAu0LHz8J+hzyV75+iMPl46ZyPperegMan9fgj7dN+0uKp9UOCHoXzzcnFt5xhwNPR8or0seFeIvppKb7dfkVMgI1KrFCyH1p7t8xIZvYNPJKPO2xOi1YJHPJWmr0oymqSsoaWuvTr4yh3pcUSHqW2rwWNKtMi8an6IYtzQhiDUdp1VTDjS98fJ4ip96k0sWunqysBdoB5H3/G0LO9F979Arfw5HQ/IAmTospXU0sNM9eSYjdZBO0srXWx2JUynK908a21rnnx9y7c27tZ2nzWqv6XmEBKS4pGEocL8tFVpPEFahgUBGQeRlzkyaE+49v2gjVgnwQU0YVI93haSAZXnkCBsUBqFYN7jSpl5lqZ28Zr4E/Da8BhfMPRx7mzAV38wfAKjBE8AmSbz+0nfXfAGPcaBg+MPUNpDrXnk0T/aUzpw3wWL7h6CB4HEpnc22x4sk7j31uMxwRXdyJt6kzEk58HT5xLsXLdyS+vYexZ4RPSADlycTXWPO7MwKrjXtaDK3VPuWlx62BKcn4Tf0C0fZ4dnC3kNFcJ+w76fmWP5hsXcCl47Y3dILnFFGF0TxZb3QRhfCKdnjbaZYckrE1iqQamG9IdyMpYTajSy9xY4rrfMtdMNfjsK2ZdZnrb5CB3uUrWfusmmnh5yGJ43Ran5dLl6oDE/ixKooGcKjeP24U9UloF16kRVCSooFxHKtHiAczE6bRnULW4y89vgm72usPPcXaDaPFm1mjDKQiD1l0QR+4TdCMCHyIediC+tFoR53icvXaSbbjPUqUG7JPpyfBq3m8FMtYteT6QdB2eiVCeoOcJHriJeoBMWdXmR5ce4ruOuQquCEsPNzZqTgilkNqln5yx2AckZZYAohYlmPpi1QSlJqdl1LVemWFT0sI3qM++poGQfrAPermCpubVkAXKxdndXRnKybTFGVlBs1yrJIbRUFEcW/i848sHDvHfP+J+kAKPFrW2O50fXKJzVLLK/RHxXRO55HEqJV89uSdci3q0MCAX4ejImMWWMV9xPgLxGtmsyBUEA8E5EJ1M2rxZqxhA++mwJGwrvvJffpgswthZOn5Wy69TP7HB976AFaoWVBwm1tmsU93PbbMd8MsRPbq5EKhhFk8KVeDCIzMuDkdOlhHZ3lMUti++PutsR+QPtmbfcgq1Wn7iyE3202Bc7MlOh8RPWvG9OAqVISSw1f4yKpyl+yw9N3ZEa+ye6JGLkQjDj6KpA3yZoOHdoOGnJt0riQdKlLLTLAE6pNUVolqX3gYMYEPKU/3VYVAqU2MWucIgWYYa5Uc8E1o6+64yk2Bhuz9cjrSoHKSW9znRXeKvLjmEnuacHZ0YClft8WPwUkHHI1u4JDHaTe/T1D9EnXeJlYDGQ3PMZjoANCuUnHfBU24bdddTckUHczBHsvBePHmsu4WBLErahijGQtH0uYLvfww/bcNHktkxgQRHPBpkdsBYtabaKIoEsriXUkvItl6XRKdZN4NSPQmDqsjAOAXCoOYTTZ66GlVyYS1HKEExmvBCPGZyVM9egCK4ahWx18qrN+HAKF/I2/efvvsuCBN3Aigm4RZiq3rVLNyW1MwaIBzNaYlLAuiwh6SkDA/sz91aSeJns3YboKKIKNq8MQYDd6dY1uBx5KQoGsT1xsayRXL3YBEMUP4t4IEZLoY7q2vlNI4F/oyeXwJ9QuPfZOkPJBqHJ3Z0DeNljZsfCFoN3yuPu6T5ScbKPC+OEhWueOjZv/ATh0hX7zxpv3WSgV83Fx3Ex/RdZocGUWVXQfDR6zuPZggaYDq//oTbHovKeXgto386f7vTYc6JICroS7R28iG2om/cwbJhdgHkZeNsXHxFnqefxc7NduVeNSSQTK7a6jBk62khctDQQ987e5nJu1PuwbnTjHZCctkEZhfSP5JuNmrfukpnWB7kQPG6GzUXKJPtUYZwXVnZ0T0N3bEm8ab20KpZPax2VOkDOXSSCXOtoTA0jsB6HVmDS2doGoPMicNzsX8fZ9ybS3UZmx23K/vxXXkrSdy/I+1s5I4cR25srs3VrMMXzt77zU70+fnGuU5x873bVlwHBh7gTdfop3zsjnarz8vOZkw0pVwQlpOaxsSvtXjbB7Hx2uf2cS/nZs6sYmf807cW1hXfhpRH9J9rm9IapjEASqM0kPidF+5JbY0ZWNUtRGszRnS2vXZ6q6Bi5qHUPXN2bgobeNdWiznd7c46ukbrT/hKPx3ls8hKJHbRrljl2RIzMou4GpLryGyOfh7tnRrs1Z8MZOvq8HWDtia6MPco7JjCU8+QnePi9sKh7hcg9bRyiX6v2Zqa64eXWJEzQI7o4lLEcDrqygDTei5Q9yGh9nyWAiha0gZxcxUtY/IR5uN0ybC+oL4JS1p2/HxK7uf9TaVKHBnBbinp2wm5t0+XpOz0VlFbaybQ+f0EHo9vKfRBv4x+rFNfm15t3KN+vkFiNb8wBFHpL8B1By3jvbvRiPdgEzTPcPlVisNIkWo+tMnJYv3CNmb2360w3sjes+A6iWR65Zy7tdhnGS8XiWlu4UvjoqCTvt1VeQK/RRRPikUuKYewKj5bKfR34aaH6KQre8ODaW7KPuEOIfpvtAvRayACi8j3JBZLEQeojdD+BC1Aq7Q7WkeReHlSASggKjcGI3KpT2MJNsynHIzC3ilwv6HPIBu5gRImRQO/aiSLOq6WZi+0fAqU1GSlqe/qJE0QKYJjAYs81kmwWVnwZQOxKVVeQqIvwUVuXUAP+HxXzIA1KuCMtEJjy6lhf4V/PUNeqnvlqftIUusb0EJCF6ca6p6PUOAq4wIqJVrSxeJlq10I16qvR4oAaX6qX06Ge8jeWZoeGiqpk84nlnRJ3p0TdKTf1YNjprHw8w/yp1UsBt25Qsgpmzvs1KCfHHjz1BQUlv32E+DvA/wj2vlzeZajSdKUkabYptAUr2BsrRmu/7ZadUPCheGZX0iKti0dSuz/80369KKfjr47seQma2IsxkNajupv/YDlB22MpKqV4qdt++imc5Xh6Tqmu9mIBdcZrb831mOQidLwqX7yxNMZGZDzVFXABrli/8ylEcpu2AhSjMswe3qDueTz1O0vFB5Io0S5gR/0KEcLPAxfVKMFVYgroa3aoWj0tHEs8Vlb+LzAHqtGIq22PXAYiw0ecqC18zrf52+rIiREJ0F3ONNfawYi2oolPo/26Ra/Nfoi57bOoRKK5ghdjRxB5/t8wHJUU7Kxa7YPmAsapWLesRbypuVWL7ShoVF+o43ZBEAXArfVeq5U2n9oNFXj1h7dmh4LExjoyexH6SQJY2jlz3RslpY/q/L/C5KY8mxCCp6dfZSc8jXzn6YFs0B70WxmhIuEqEFQo+iSn4DTe26hVi+lUSogd17bOCw2hJ/yAUOCaS0MrUb+CY28TwzSskiiIH5WAtFUuK3ZEB8N4a+QAIIm9z676e90qTafJ8m7Sm+5nilLjO85EjuvCi3HX/aAgugH2XDXfoytc4ApL2G/v3drr3UEZw/dQt2IXDMAhnDTnykLrY0DR/NQzN/fhxOEafqOyUm9BEZYTwvMq8JsVUUrXk6zfEOUbtf0K3gzQWOovVVm2XVk1nrzu/5GDZhd6BhRFbVYObRQEyNL5NedITNphkwrL6Jlg8B5XTegVo4QPy6JhPfGq/RvucEC6vMLGAxkdj1uydAm9x0w+KnhB2/lwFk71xe+XZ+fbPQNtA2+tMardkOKRQi2/WV2uye1cvNMrabG4t15IBDu9YmGNqgd3bU7oiMvYr2wT/MWCb6r8d1B0+5hpPcVorNfIJvdKu3XPo5Vj5WsrrLp5guG7fedWX37oOlm457Pr7vTbMjO1qLPw4c8Tpqr6XZsOt7Z2fTo7PlpaokwWh3iHuG0MHIk6jO5Jp1Q1OZeAZ+PHfdP3ZAtshXj1zUe+wxaddLyNjAq5yPHJSs3FLd1NaLUAa6HrAs71AsG8lOwTwqJMZVPf0NouL3/J0r2StLgAGJXjEjm+zGiTsYhYj3g1KNGhAtg877noGKNYyzy0DZsw6y4u8ObnzffWAvFDLJbbRAm6sTJSeQ+W5XxL+HeBZBD3xQoZs8C8v71z0QsW2h7NDT/cAuQ1EFAE0LQD3u0GXymY7+5O2gTRGhzIozrtAn7Gi8kQnEAjYAHDzIOO98jTsEAhkcxwK8CSIbYDrifomAvJOmHXJVwN94AARhMGAmMJgwpj/Cv9fR/414X8d+dfr/5OR/wjwfzHt/4+F/J+n/d/9/+/+/1+nPYFb2fOfBQconUsroN+P/+2I8PG/HfmP1/8nI/8K8F9H/ifTSsf92hnffy1vNPOPGhDwu37N8mqR0Z3H/wZQSwcIJ6XT8fIhAAA7JgAAUEsDBBQACAAIAJpuMj4AAAAAAAAAAAAAAAArAAAAYjE0MmFiMGFhZmZkZDBiNTZhM2U3NWJjYjczMWEwYmJcZmV1ZXIyLnBuZ+2YZ1STXbbHHwVLFBTxtYCYUAJIFSEgRZoISVRAqYLUV0jACNJ7ExHGAqEImEgRiSCJAQViRIQoqDSpgaC0iNJD6BCKwH1w5n6ambVmZt0vs9bNp7P2etbZ5+xzzv7//rl7yQwpuEd0DwAAgmjUOQsA2A4DgG0Fu3eCkT6fkVkAEK1DnzO0Cunh9q+UWXVV7Py+tkvGGp1yYichPYbvXKeQyKEdxgcQ97bfi9kda5IldED2kkASxMzQ+EGsgLy80G2MA30gEJd7Xbsfa1CjFZJbeL1bC8ub6hdkTNKrF6m0jUIAyDLc/MkAAE2FmjrGxmJJzk/25kZwa6vY5q9RfU6KPztqzUvL98e5VnWtXHZ+RfW6pnUztjwq85YY8F5oH4y6f3VkDO76k1PCUI5e62WbhU3rb8zic1Q6oEfNdg3yAVHv0/H8f1meoJQ0bqyvNSFhkVbRUJ2gFznmbfXTWrxC/fWid7/mmoZp3U6UaPquZG+JkYB4vHf6AcBldwLeJnqd49z06NS1xjjIwcbOIsum2B17G4cznZ1MksTsNqsnyJQJ9lW6t1JlEFf+sYYXuXvoVw8N15QLrn6uP5idzu2lZ6Yr2GaEzo+kG98/nE5nR10d5gPi8Jv+Gyujmc4bc5nDS703Tx5x8DG0Y0RFCh7atU/sRMK+4/KVwdPK5vrrAXZ0b0cRnaAbBJ1gb0GR0PX7J6ufdyVYnbd5ceXytP9wum2GOo71cG2awegLn64aXuWUnAzuD7QNnfmwqwmsipPe2qQaWIcNRjyeUlL91kZGuXKyVPSMMFRYNSd6Y2VuLB/P2lN3Da9rE13wI+X7Kf+RL3MU53WyonP1uz6/JqXhvASo/H79Xz4V4wWPG4ca0poCux2DLXxQKg0r7I0leuDzke8fbvOtJhV2hOwBsj7MtHff1jJSgPxxxDnCN3SxyxbHNpE/zlhpvnl9txavz59z6XyscRJ/Upb595Clb9imHN3wibVC81wnBYkjjgGX1wlS2zC18YI0yQ7tY5ifnxPVy9/xBsJ1IyXkYcAM314YN5FkuijOkL2h6PDmZYsD+hKK6bG9Djy+q0af8FEL+X4tWqOd94xrjOUly7CtxYxRh+KqH/cUGo8H911WEE2TMZU/4hTiSg0bgpa8mztP9SFpqVsGOEfMfprjOG++XYoqb703jvjEW4MC78UT8EuBWnorQ2miqh1Hia5pVqeVqxY6egpnwRvAcn1opaPamQpNls0Jearo+LbcRt/kwdHLxy7JmmVd4TPejl41Dpr8epki6XnRtMxz9ZxTyOCdntFT2Jas0hvfSkVNerpnPNa/iRpoC9IXTj8BAKxKRHlCEmtX8HZUQZMJ5jlc0+05/JbEB6nBwZnBWvUb8EsOfg3S6i6KTu/enAELSbuFMJSeblrhT7bSgYZ8vzU3lGbO+rnOY5ekJ49UaXXsT117nZA/UND2emeB2SYUvAPxl5bHFsRvJv2sw3cPJEpfyOgseilytqENTRYT0W64kc6fIEAZwtaga0zCzmGaidbO5tZwpq+a0unoUSxZoiLo1/IsjSGVSJkfbS05lNEnKzH8LNNJfvrdvFm2EtPr6zP6HtRBk1X7NT7gaNxMu72uB3cFFShl6XpQ5nPiMdvbn0JHs23jBY/ZPDY9CDfBQx0poqFKefCyP4UV/YamEYUYTZkq8QpkUhw+LjMugz/ZIZxDpbMWDfwYAt1DegSttPFKbt7zXuHp/uLLK0CMhLCetvUBIpDqT5gi5iVbKeaEjhBE+W1KnPotx+vDjlNsqOT78cO8hVD4Q/gV+LkHoupkG11VinSkmFbueWSUeQlK/hhEuSiCxP45Hb0Z7qXXzC56dGauXmpRp7wkvkcpIoASvxsGqMTVIjkVC/6ksBSJTNR+FFlC5F7FYPyxxtHcaKdWrMyXkebHuGVUrYdT05p39cqIqKaFFvpr/YzpWWOy2NXXN4ru400Jqs8m+yrKWp6ufL+9f0KVKxJUMd+iw1FfqbR0z6dLd4bvla3ZBQj8uTzG8iBKVXa0PDqVbyPfYUCUe2VXJmWJUeuV5oTBxeEX4S59/q26w1OV08WukrhAcE3VeP5E/vtWFzsciDvqOnRS2UzL1B2NczkCTfB3JPnUwYyLtPWRxzevq8MHC6pWU+a5leNB5Htb+/pYgyz83i5Q6bbYAU6gJgzveJyirissZLF4VC8i5LhGg8CjXu9K6sbFma/0m87Hn6I/kSAwyF7IKQhCK1c87Zsy4UBaa72Qabx/aQsyPqT0ud0Ak8rOj3RMXXrfTj1CohUa18oBAhbLHpGaWA9p5EEDYUnvd7Of7QkoH1RMfWMhBOIJNfX3IJqqfdLoNpE/9A2h3IXfap2LHmQBiOQ4XwNt/CD6mme8R2nJBT3ZbTKC5JUsKWRSgIDIOli5k6hCHBCjdlRvlanQfuYJk56yeEZVSlohRcNV0uhk0RWScOr4K0J/qkwXfxoiu3ptqnJxVaCXZAvfm/zsCNxQiokrG6hLgEVdSbgirGFhjW5Dl3m2qBspVFkj3i7GLXTxJCLAHnAHvyFgTlJN8XxFWEmVyFCszNnAL0S4yfbw43/lSDP9vbafK/hRoA+v7BzpsdIUvliq4x3vpPowraBjUiTNTgmiUaEnUfhtB7335floG30udc/TUfAlGoAvUejmdoOgLNNck6VQ9EsU3qTGKBaJKXKLPx9/SdVdo5lkB4NbpyBSMCWZC4luJ9w3N9YDw7xXz/g5ZtiaJ1dMV69NFFdAThY9DZgwGkfceR0Z5rPWvlG9NA+8FxGAZUMb+zEPEB38xPGSIgt48tD05GzqPZMaE/mjN6tXMOYMFKbJwb9ZfXi2DqY/foEkR7NzUUSuGvjhq8J5GflI/JL93XEva5Z3d2A4DPCJr0XSX7Zzp806XIhFdM8zzZMZXr2vu+7UCZ/pIBHvoZdurNTCNi6taZZ6Oizd3NIrQQWIHATh6ZYYR/g1cNUcGV3QtYRtVAJUdqfjq6F963Zq+QR7Ha+ecvuG+raLS7caBhQhsuPDKOZ1srhITsP0uKBnt8DdhWcl7zvZw6xtW+f8VhC5oJFIi1RKroYOcUvUmSHha/sK1f5YoMnL/3VeUbPwxz+025QmwzmM5ZtxsdXE69tiJC6tjJnDUNEafhzc/gy1V5Ohzh/2AEeHQKUSHuYyrcM5e0Xqp0qxkhEBq8UgVUBg2TaHvDarenuO8Yl4azHT8RtfBrYBLS7LY39oCqsSTdp/TdqcGru5PNYaxCu84LwuB16TOLz33kB1VylL96uwzlCl0dJST9Zo/VuxiqkAqzNmo8mom1UK8Y6AS7ICyCxDL+yJ+Sld6DKxsKDC9XHzaHtQtLLeJtWBdDExN94cBl3PbvCTN1IrtKeOlUfdndkG3P5D763uo2N27ojKppzwqQr3ofqUwJX5Qwo2DwtzwsiTX1/lO/W+OC/av2Sr1VVEN10cXhNoKrfV7Qm3A2IMn0eUn3aBavo8UU7P6ceWWXpp3Md1vTtpdDI79mzhYCIrL4vFo3nPscY9wi7aT/drf2TCqvphv9u43sfZHlxJ1+BD6lV6Bvj4FqyEtE2rvEQvr/UcK6jCk5gt5VzXZ+seVUHi9+PcdxcxJ48LFoKnMZi/bpjVzC7d3MKm8HirMIpZuTndS/Aw9wNJK1eljXqSFHniBM+DGhVAvKsmJL/VaOVhKY6YYG6P9emotV/zreZ75LLJQlQj8WbFRyMSm1w6m/WkHarnZ1qowvQ61MGaaR/gU22baYeeA7coAKPWCn2781rEzzOyTVazvHhlFgSwrtxEVkxyt7BBj8LhlcpQ57VROi9xiIdZMqVz7uwGNJtqkdtrH4ioTbQOkHdCJLeAq2J1gtL0UM6ykYROa3xhV7aRT24rqnsaGsmujnRvylAKPNw8N9zU1O0c3X/wT3sGdj5Hpi+CLffm9yVYAjr4Y62kR1qyey3b62s3tmitzEVvfYHpB6pnWNTGr5XhI4xlY2pqX8jPRPelyW/uX1+66h66uwsa8uQGu3qdBJRiW3PmvmFzu/yLMG6rU8uzPzmTxKaTjHeKV1+/GA0fmlfrCh6sueMOcvTmbDaXuR3A+g7nrw/qgmThx47kpYO8yWo0IYte+/xATsrkwYn5kWbKNvgHqb0PqhZZV2m2Q697vSl7U6QRWZq+TzWoMg8R1g947GiGg8+HHTRyalRqXBqnuLJ45wOrSwPgIv2YpqcXIzIDOax0ULNKfk1i9SmcB7+mghkK7Ij55mgry7j9gObeWmQSf2xczEhebvrFsqfjILI0fbx7kNN2niyWJmuu/Pj0zWKJH/joX9dCx59lTggQcn8NyaqThpzs/HQHr3F7aLpGkhTbEmWQ+CgSI3dlc55TCqrBfO7TA1WL/iVvJ8hzoIqxcGp/pE0nh2/h1gCvTn/DtwJku4nUqWyNSj6gpXQmZSfzxWzKHuMwFWET4jcFbunMV5DcrxugpOEKOa+VG3JUfEFkZuUR+9a+vrqmrun2SFpCZrrVXhKiAoHfP3JSGURv8nT/S1cjEd2wgG/lnkx08wuqxTatkBmX7H19Vrrapl07gHifZQ9S+8KrOqhCdjEOutCqt3aDalVeEtVTz2EWmk+LyDSEg112RPV653NRhEUValgqEmpXXKX+hnQ2dZCAyA+y99bFtGTZKaiIQBvbWm7v1wvpYAwyaBeUAR/RWuR8cksy2uY0l0sUoJFKU/agD8voRCzPoMuudfClusxugZ7LLNi4u1VUQcS0l27Awg0Qh/BWKh1jojrBUy8GparEIXLZS9cawi190frnybIVGxWjORTeSpPzRoevvTKgcq62DvRDuHRJ16e9IzdNAbQ5stj0Zb3P+TAjVbEyj/anpb4/P5de7yKDao1quEj4EtXwJUOA4XYC0/vay319dXFxEVEyokdQT3P0V1NME1Fv98JciDUlK0COI/FQKuM07n5EruD4b322aHik4WVPxQRUFi8a5hCUxo+g0yWR8Rfm1HBBcDHS0/awdfB+OygcvpChuII/mTkz02Xr3JWcmsi10B1/bee4pnKBUl2tBjaIGmTsOdYA6tlT+q4VA+gIlZIJYgPhWwfXCaJEMEyT6SqYa8/N7+UhpHYC8R7LHtA2z++TXl/dnyDpcq+yWRyPFneNCxh2QBi1t0qnOeQ3Rh7V0za9zKXGtvXerlonDpAP9jvhuBwP9rECJm9sqUo7excQf2U4nz7T3psi/VXN8llJI3KtgtU8qG3K4eJQ7k92ASqowfySXWHRYSfsYWOECaKdPB9EmVpmO8XY3MhJHCaGY6qSWf7r69X98tDtuwGB9sa6IquDpbzGT0ec+zhVvZSjKXKlsIgZQ8dD6l1prJmUgs4X5T1Xr0yU13o5p4uBqlGLdE6P3RDDsV7IZToGfYupRRZ0662O5QfmVygKsUT1SjNQhc1DOy2eeW7yyqP1AJ/DNnqluy4G0ZqVaVTDPP08ceZ1NTd/Xn9wbrlYeMFPDN9bTHbyQM3noqU4ADBCRAT0lFZX3fOdruKxANW2gQeIrGqwD7pP9VWof0TkfU8z1ytSyNPg3A7YgygU1rbf5IJCKQhLtJJLguk7JSB7YBv0gTBc6FheglnR9VRdF2JUiswYqTvfzu3F1bajqGWPzdN8W3k+gibVdgq8jH5cWjdL19beyJB0GTG6ZUWLayWp6amsbstvVyr83Pul6eoRkz00DqlVq/+vJWZqixIGegRu3Rh4V7Ev2k2jsXK6+ioP0zBNnTYdq1emF9ksqDsw7Rv+MhmjEzjRWRrOm8q5lOyf6eCHtqsKCzQXH1d6n9V4nrJ1BLcakfM+LR0TEFjKpdnBBNhSn3hv16gH9IfIPbu3AZ79Va9pWuW+39/fKgUbX+m1uiTtZxrddBtNjRtfLwV/bl55d5Ln9MbHdcsIhGXYTrduKJJBTDocjzer23KawUQvqkG5dtDkFYJueNC3UvcLrZGPcae9eqxkzHMcCi4SLCiyW3ZXUDTU3MlcBd0ldf+ueodlav+NMsaXgapwnam982vszeozG8s/F+sR/Uho6LllIAZ2dtkj1mR7Dei77PlM/L1X5oZp5tdGvhAC3Zkr86OZoD6lg/Y2791cowLtT1VQAea22sQ9JBnGYVEpulJrS1xKFRTXXawE6lek+Sd46QBSTwEXgTiUoRmx7EPQiwwTVIOo28Uo5qbJN4y153NoW8ZkEBRZg7BeI/fWHF33D7E73EExc+8iWy8a5rqm8N/iv7OAHXqk4npWUBKslBJojKLs3oX4Olb+BFskpSslLs5Kgdja0tkH4krWgp3nDVMPT9CBz3tXDGeIxr726rWpvXDWbErL98fHrbaTJq/2O2kjstDRvdcZj8jD2JyP/bS6yMHRfoCdQvH+YSXyKF5My2LfcW2rY0g2qFL27ai/1J91heyGKBPuPXZKxUTi4xIQ6RrRo/OgEkygpAzhvCulbmgv72w1rFnFTM1eTo84RML0DokBXqyZA8CM8z4Y934gTS95P/TMV99l6cTnwQOhWEHhZjYh6rFKh3LZnxY70DQp61RWQRfqa31yM8gjURYe9dBTFdEt2HTm8gLTHJfu3lPuuYglXlXjfyiRjXnzLPDwxWgKDGQDK70enl3Dn87jhfXk/NCxYLLQ0CA7q9WqT4D+5fHpadJ1Y3lpiNjWHy1UC3jcg2Onizdy8oiKn3JcQb3AIHtl3N4t/7gfeKAMzFq5M/tyvkn6ASmTh6eufe4M1Fed7DhWC2pHRhweQ8TFozs+EqIeKBI2Vjkl3Ys6HTOExdN+ymU2xITgVUOLZ/UV/JnYnNCCnUm44oqC6owJY1EjJjys2zG4y7PCE9HcKlBIOhAIAuaiQ82Fmk93D8qGVc+0ZOvg1OHbpNNT+bO/+DSsrK/xuvNyHdhyFxew82cAFyFQtgzMbnuQhUV+oKQ8MbQhLBFleaseR+1K5U/6EoA2Gttigpeutdff1P/RL1CCOHR3IXxolT/+V7ZcmcjbBqte/syFGLjL0DzoMdItr27BSiDZO959Tlf1hZpnB8kejR6WVvOxuIt2OT9sPAzqfepMe9wdK0nVNfj+pS9BdmUY0+NJnktBnsXmoJPTX+y0pJ1PAevQkDPTLtAaEPa18Gzqy2Tc/MbkfiZ/Mn/aEs9NohRRhjnSF2EiL16B1FNzlf0At34MTtRVxGhmGIEvTkJIb3Ui0SN6DIsqsC7EWX7ycL6Zf5UPFBJNWU4ovNxtWXqtwm3pvPxJCGx8DcWuR8IiO0FIMa5/fZPtRFEKdcYw3K7INhc2q3xpz0fiukgl09t+tx96URFfJJVRZv7WUyMbF+/1VunVQJ/sIInwudfzmk46yFT3a+qKdqYxaZxJgzWNL0HbtrSqp3tFs//WtSeUxH2fwXkshn8yDghXT+uaYwMLennbgSiDwZ8BVtLVrcEcyhHj5d9gjO311a5mVDkC3xVBSuZpHeMTBGb4yBELSyLcksVFnoFe7cBvJNgFxIBWYzcMAMD3Jx4BbA3/cWRr+C9G/jbB30f+9/O/j/zTtP/GQv6DtP/GQv5///+1+4+ZGWQAgJAeAAzyAQbLAADal63hP46Aw38c+dvn/0rkbxP8feQ/SPtvLOSfpv0/Wch/zf6/J0xHb7PJIN5oO0fxBMAf2tjsXPFZl9j/AVBLBwheKJ62YhYAAAAbAABQSwMEFAAIAAgAmm4yPgAAAAAAAAAAAAAAAAwAAABnZW9nZWJyYS54bWztXNty27gZvu4+BUcXO7s7FY3zYdZOJkmbaaZJY6/TdKZNp0ORkMw1RSokldh+qnZ3n6AP0GfqD4A6HyzaykGZXEkEQRD4/u8/AtLxw6thFrwzZZUW+UkHh6gTmDwukjQfnHTGdb+rOg8ffHM8MMXA9Moo6BflMKpPOjQkHds+Th9887vj6qJ4H0SZ6/I6Ne9POv0oq0wnqEaliZLqwph6oT0aX6VZGpXXL3s/m7iuZjf8IM/y0RjeUpdjaIuHyfO0mlweuReOsrT+Q/ouTUwZZEV80hEcpg7fXpuyTuMoO+kw5FsIrEurhZvQRO3di6JMb4q8tt1ng/ehJQiq9MbAk8S2HR+5hR6bcZylSRrldjFuHtApCN6nSX0BfZHEMKZJBxcwWa6EHy4uijI5v65qMwyu/m7K4qSjRUgJ4gKe0FohBbO79ncIJyFRSgpKpEKUcQkgwoxhKhQe4hoRjQTlWGrG4KnN99y7zbtzU9cgzCqIrswM5kGZJgsXz6rHRTZrGhVpXj+JRvW4dEygTdN5fW1fB9CVdpWP8kFmmjYCgrow8WWvuDr30FE/9KvrkXvETag3eFJkRRmUdqkcOjSfPf/p+tiZTnsh1we5Hs0YdtDpfayJ6+E+e/7T9crS3E+tWTmerBqjyWvSKrANMLgl8HTxWdQzQIhOMM7T+vnkAohz2SwV+wf+Mh72QHPmqTMdE+9rzOOjJdIdX5oyN5lnVg6yHRfjKnhnKezf5SaSmDgdwqW/0UASWXH9FSbgWxMzKM1k4l7vPGDuLppn71Lz8dFkEnYOFcw1rsGAwHpquxar3zXolv2WRLVtscqTmaEBzaodHxydprg86kzNSOEswkT3m/tzK4P7a8nhaBRlo4sIWsJm9ll0DQZifj1uwBdFsrjKKAe03BJATUd2ACuPkTFJYxTrhsTBCIZ0KjE3JYdRFVyB0oecMCGoVJhJpoCS13YAirSUVCCBMcfINt/4cd3jXrOsJXFToo3YPVy3APf022hUVD+uwrfIuxlDQV5J6lcK3V82vYv9Yfuy369MbcHogqbZ9RP+kaAHc4nADEpMCEXUvbtLQ4EYUoKCDCgnnO4P+ydfCGkxCcENIUKZphJxxL3UQqkYRRz8E8FcEdUSubgYDqM8CfJoCJM4NwPb7hBLrXMPIjRjbxBhC6eHalxPbkd+zGakFWlUzZgTvKPOot2vL8C85qaqnHOq593QFlXZIDWOndjsx33lNkO+C25bKaoJxd4yYAe9DIlgHIIWLQB4ySR30AsMFFccZKSA5ByrZUe3ZcHmbe77VN7dpEOIoOK0nmKeWYI8y2twPsYZ81WfcmnMyDrzl/mrMsorGwr6PnO+aoP4fypq8APbpK8Bxh/++2+4IOuocNr03UqIRfU8bWsa58UtmBO3/ej5j/tLG+sQK8lAmRBTEPw1FoqFzKoY1VhQITTW99EzF5Ft1zKH8ByeCzj/7z/bIXYhxBQ76G2fh4mNm+kBRSUEtRC+CohCgcDiVoVbLwBvJTGaRH4z/PGO+OMW6hGV8RzEk8YsK97/ZPqZuXKw7kr29bbuicd/E/C9draud3C2bp1RA/ovW0BH/i7GKJSCa60lI5JTzA7H1u3g6h6tiD9uJ/744MQPZk5j8F7axxhUeFfXhSGRBgIozIULmWnj7YgMsUBAC80Jgfjti/J2RM67u1U6nLV3d2efxN3NRfvEZztkNz6gUIC2I6oYY4QxrptUiYDOUyo1YkIKcCL7doZni3ro8H+6yRn+0soZ/nKbM5RffeFaISzjnrQzhsnhGcNlq4eZkk4B1ljJmyZPwMIaRwGU0gdkC9cT4HSeAGcb1M+0o4E5PBpwyLERZlIioSjjTHifiBUYDiHA9QnEKG6MIDhEIRXk6YghazD54ZDgRZp4Z7XFDGwKjF+0cYIvbinJfLxkT4dKawyqSphgiGjeiDbkGiSOkCCaacHEvepR6TAazBb3OM0S7ADopyBqDz3v66TPhJCIGtSPpDGxShKCTCR5T5HkzXlt0pyEo3zgZ5Dmj6P4clAWYxDfgnzBC/SqIhvX5jwujcmfF7EvP8FyCVVugRxZJ3cXNdxBTot7ARMh4bZC6qdXJtlM3dsgJssQR5HUnClmZF+hBFIWHuPYUKYjgSIh2Zs/pvGFuTfEnHoOMVdP/aIhpssQ9zAjUQ9FUb+fJKjHRUQN8DfuSYoj1Ou96ZuxKe8NMdW+JqMk/bIgXto0uJOVvP+GAPMx/tYMYV9FbRUKMLBIQTAlIaSSZFJsE5hoCnTStgSHm2Rzd/t7NSqBBXZ+k4ChE0DjSee77nc4ZOr73wckFOr74IfAp4H/eAQtTbr3z05wtCKbfDw0ZRrPIpDlNKKLRSjB40MOLMF1ECXVrqxqMoTNnvk5MHw5Ud0Ulg+2e2KrLNNFDPYSjLVRoPvFYZoQF3D73SMx2TvCEkFy6qMwbivulixUhGAgCAefqggHieyrONW2orBjLaFVFeHjBlDzm4VNBUDtKDMUQvqEGCac2UAKAqpJ9BwqEBhkSRB7QajFyP5rCIvVg9W6wa+t6ga/3lpEV18LBx7ZRx75Vcgv2uWKF3c0T233d/dintZbpw3GqfvBrNMnKxY0Qj9bEXraTujpIQl9RbzeuK1wQXip61ByiSlRkHIKyqQ4dKE/3XQo4Od2Qv/5kITeleDUJKGSgc2WWDcFIRZicHR2e8yGskJ6TVc0JMADBPTAXAh+QPWgbeHMbQcB2kQzp59NOYiAy9UQoiCNqJRCz+pBFEMYozGBRqls+WTfu/+L+/6rwcpvrYKV377u+Lfd8V+B/LKdCbs8JBO2bKt0c6Jp0a75rLsrwcsRBjk6ghjengs4HBO2w8bWasCStRN89iF3NCbHr73sMSJ7ilrscUsmlRJCI6HZxMwhpBTjSCtNkBLNMcyu3QVWmnMuMCNYsNXD24fGgNPtuxnDdgwYHjwDFN/OAMFDzLViRDDKNJeHLv+FYx6reWreTv75vuW/8/HvD0KOZRIwNkllV6zGjc17FXy3W+Nuj1QdvG042xQQjNqxYnRIAQHYeM6QADvfpK1NoQ8iYq4Z9YfLJfUipyq0dTstwBcwCT7hcER+WmTXgyLfIPKpVSDeRdDNxx5ep/CK+BL7J43v9S/sn+3NXdLpXbhg03u3JUh+mhMaTN/2UQzN2zWGBrENlGO8Dec2b36tHBSZYvghnevGZd09h4RgyZ6H1VhhwZkUvjqAdcgVZ5CFcf8LFx9cU2nPlWtQPUQR0/Kz9qy3HHY+UIF1NwRDG2KhQwqFdtKwQxPXsoLJSfayXsOIDKFBM8GkRsT+VupwJdY7SIl92enm6lmDV+aqxs15g2/fjov6xz+lWd9UtcmycT4IsG90Ay3Ku4YnO4vDfMrwsKqjsj61tc3A5QUq5ERxSjCIRCEuvWfjoWC2tk0FcYWjhd/N3o4UWUDqz/6HypcuJjEg8DK4eW/S2uTBU3t4yIFodgeQ7A7gnX5zu0d07e/OFAAplSvBNdgiTAFo4k+USME3gruAQ68oMhPN4sdiuR48t+6PxK7ZIQIp/ClqzjbDcztv6BYNI7sThH5uGsYhEgRlotrq2HRnCeykxEISl6HhdhrGFpD6W2qCS0g7QKPO4Ws07gdJaipTBadRGYFyZcWgjIbDh7tjyO6rZGsSjg+mZBACCEKk/f8NxSeb9PZXLhDTNef5ubyblr39vLTMn/XFSOymZkfzfxJhryd/J/Pg/1BLBwh6E0l77goAAIBGAABQSwECFAAUAAgACACabjI+tLJ2N4UgAADvJAAAKwAAAAAAAAAAAAAAAAAAAAAANWY5ZGY0NjY3MDNlMGZhN2VlYzhkZDIwZWE3NWI4MmRcU3RlaW4yLnBuZ1BLAQIUABQACAAIAJpuMj4npdPx8iEAADsmAAArAAAAAAAAAAAAAAAAAN4gAABhYTc5NTQ4NGU3ZjgwZDk5NzVjMWNlMzQ5YTYwYTY3NFxFaWNoZTIucG5nUEsBAhQAFAAIAAgAmm4yPl4onrZiFgAAABsAACsAAAAAAAAAAAAAAAAAKUMAAGIxNDJhYjBhYWZmZGQwYjU2YTNlNzViY2I3MzFhMGJiXGZldWVyMi5wbmdQSwECFAAUAAgACACabjI+ehNJe+4KAACARgAADAAAAAAAAAAAAAAAAADkWQAAZ2VvZ2VicmEueG1sUEsFBgAAAAAEAAQARQEAAAxlAAAAAA==" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "true" showToolBarHelp = "false" showAlgebraInput = "false" allowRescaling = "true" /> | ||
| Zeile 16: | Zeile 19: | ||
| + | Okay, jetzt haben wie den Schatz gefunden, aber mit welcher speziellen Eigenschaft der Parallelogramme hat das jetzt zu tun? --[[Benutzer:RicRic|RicRic]] 14:50, 8. Nov. 2011 (CET) | ||
| + | Super, dass du den Schatz gefunden hast!! Wirklich keine leichte Aufgabe.<br /> | ||
| + | Ich kann dir auch nicht sicher sagen, welche Eigenschaft des Parallelogramm hier direkt angesprochen wird. Ich vermute, dass man aus zwei zueinander parallelen Seiten, du zudem noch die selbe Länge haben, immer genau ein Parallelogramm konstruieren kann. - Ein Satz im Parallelogramm, der sich beweisen lässt.(Dieses benötigt man ja für das Abtragen des Winkels.)<br /> | ||
| + | Die ganze Aufgabe hat deshalb etwas mit dem Parallelogramm zu tun, da wie du richtig beschrieben hast, da zwei Drehungen um 90° durchgeführt werden. Gedreht wird die rote Strecke. Welches sind die Zentren der Drehungen? Zweimal eine Drehung um 90° entspricht einer Verschiebung, die durch das Parallelogramm verdeutlicht wird. --[[Benutzer:Tutorin Anne|Tutorin Anne]] 14:55, 21. Nov. 2011 (CET) | ||
| + | Die Zentren der Drehung sind die Punke "Eiche" und "Stein", mit welcher speziellen Eigenschft symboliesiert das Parallelogramm die zwei Drehungen?--[[Benutzer:RicRic|RicRic]] 21:00, 21. Nov. 2011 (CET) | ||
| + | mhh?--[[Benutzer:Tutorin Anne|Tutorin Anne]] 16:33, 22. Nov. 2011 (CET) | ||
| + | <br />Also heißt das, dass wenn ich eine Strecke um zwei belibige Punkte, welche den gleichen Abstand zu jedem Eckpunkt der Strecke haben, um je 90 Grand einmal mit der uhr und einmal gegen die Uhr drehe erhalte ich somit immer ein Parallelogramm!?--[[Benutzer:RicRic|RicRic]] 21:30, 22. Nov. 2011 (CET) | ||
[[Category:Einführung_Geometrie]] | [[Category:Einführung_Geometrie]] | ||
Aktuelle Version vom 22. November 2011, 21:30 Uhr
Im Seminar "Computer im Mathematikunterricht" hat eine Studentin eine Schatzkarte gefunden (siehe unten). Blöderweise ist auf der Insel die Feuerstelle bereits verschwunden.
- Können Sie den Schatz (Punkt M) trotzdem finden?
- Können Sie beweisen, dass das immer so funktioniert? (Es hat etwas mit den Eigenschaften von Parallelogrammen zu tun - siehe Hilfestelltung)
- Ich bin nicht ganz sicher, aber es fehlen hier doch einfach ein paar Angaben zur Aufgabe, oder?? --LouStick 13:30, 1. Nov. 2011 (CET)
- Ja, ich verstehe auch nicht, was man an dieser Stelle machen soll ^^wenn das vielleicht nochmal jemand erläutern könnte... --Miriam 17:18, 1. Nov. 2011 (CET)
- Also ich nenne den Punkt am Stein A und den an der Eiche C. Es zeigt sich die Winkel an A und C jeweils 90° sind. Die Strecken A,Q und A,F sind konguent, die Strecken C,F und C,P ebenfalls. Wenn nun also der Punkt F für Feuerstelle nicht mehr auf den Insel vorhanden ist, setzt man zunächst einen willkürlichen Punkt F`.Diesen Punkt F` verbindet man mit dem A dem Stein und C der Eiche. Hier zeichnet man jeweils im gleichen Winkel 90° eine gleichlange (konguente) Strecke ein und erhält an den Endpunkten der Strecken somit die Punkte (einen davon habe ich F`` genannt) welche man mit den Punkten Q und P zu einem Parallelogramm verbindet. Nun misst man den Winkel (auf meiner Zeichnung den Außenwinkel, der Innenwinkel ist natürlich auch möglich) an F`` im Parallelogramm sowie die Strecke F``,Q und überträgt diese (Winkel und Strecke) auf F`, am Zielpunkt findet man F. Somit es es möglich die Position von F zu bestimmen obwohl F nicht mehr da ist und somit kann auch der Schatz noch gefunden werden.
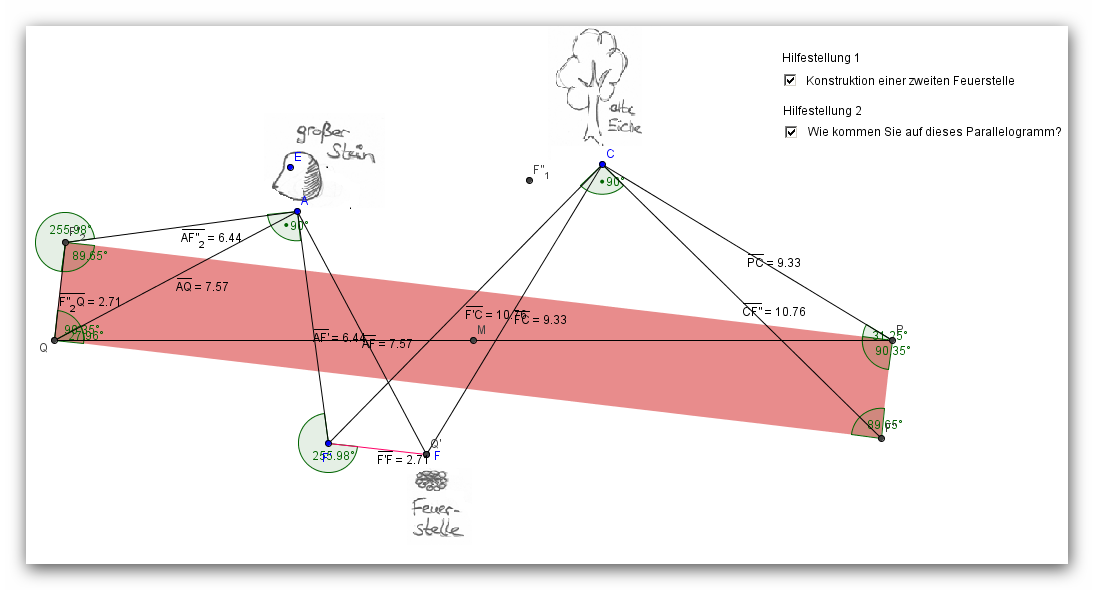 --RicRic
--RicRic
Okay, jetzt haben wie den Schatz gefunden, aber mit welcher speziellen Eigenschaft der Parallelogramme hat das jetzt zu tun? --RicRic 14:50, 8. Nov. 2011 (CET)
Super, dass du den Schatz gefunden hast!! Wirklich keine leichte Aufgabe.
Ich kann dir auch nicht sicher sagen, welche Eigenschaft des Parallelogramm hier direkt angesprochen wird. Ich vermute, dass man aus zwei zueinander parallelen Seiten, du zudem noch die selbe Länge haben, immer genau ein Parallelogramm konstruieren kann. - Ein Satz im Parallelogramm, der sich beweisen lässt.(Dieses benötigt man ja für das Abtragen des Winkels.)
Die ganze Aufgabe hat deshalb etwas mit dem Parallelogramm zu tun, da wie du richtig beschrieben hast, da zwei Drehungen um 90° durchgeführt werden. Gedreht wird die rote Strecke. Welches sind die Zentren der Drehungen? Zweimal eine Drehung um 90° entspricht einer Verschiebung, die durch das Parallelogramm verdeutlicht wird. --Tutorin Anne 14:55, 21. Nov. 2011 (CET)
Die Zentren der Drehung sind die Punke "Eiche" und "Stein", mit welcher speziellen Eigenschft symboliesiert das Parallelogramm die zwei Drehungen?--RicRic 21:00, 21. Nov. 2011 (CET)
mhh?--Tutorin Anne 16:33, 22. Nov. 2011 (CET)
Also heißt das, dass wenn ich eine Strecke um zwei belibige Punkte, welche den gleichen Abstand zu jedem Eckpunkt der Strecke haben, um je 90 Grand einmal mit der uhr und einmal gegen die Uhr drehe erhalte ich somit immer ein Parallelogramm!?--RicRic 21:30, 22. Nov. 2011 (CET)

