Auftrag der Woche 3 (WS 11/12)
Im Seminar "Computer im Mathematikunterricht" hat eine Studentin eine Schatzkarte gefunden (siehe unten). Blöderweise ist auf der Insel die Feuerstelle bereits verschwunden.
- Können Sie den Schatz (Punkt M) trotzdem finden?
- Können Sie beweisen, dass das immer so funktioniert? (Es hat etwas mit den Eigenschaften von Parallelogrammen zu tun - siehe Hilfestelltung)
- Ich bin nicht ganz sicher, aber es fehlen hier doch einfach ein paar Angaben zur Aufgabe, oder?? --LouStick 13:30, 1. Nov. 2011 (CET)
- Ja, ich verstehe auch nicht, was man an dieser Stelle machen soll ^^wenn das vielleicht nochmal jemand erläutern könnte... --Miriam 17:18, 1. Nov. 2011 (CET)
- Also ich nenne den Punkt am Stein A und den an der Eiche C. Es zeigt sich die Winkel an A und C jeweils 90° sind. Die Strecken A,Q und A,F sind konguent, die Strecken C,F und C,P ebenfalls. Wenn nun also der Punkt F für Feuerstelle nicht mehr auf den Insel vorhanden ist, setzt man zunächst einen willkürlichen Punkt F`.Diesen Punkt F` verbindet man mit dem A dem Stein und C der Eiche. Hier zeichnet man jeweils im gleichen Winkel 90° eine gleichlange (konguente) Strecke ein und erhält an den Endpunkten der Strecken somit die Punkte (einen davon habe ich F`` genannt) welche man mit den Punkten Q und P zu einem Parallelogramm verbindet. Nun misst man den Winkel (auf meiner Zeichnung den Außenwinkel, der Innenwinkel ist natürlich auch möglich) an F`` im Parallelogramm sowie die Strecke F``,Q und überträgt diese (Winkel und Strecke) auf F`, am Zielpunkt findet man F. Somit es es möglich die Position von F zu bestimmen obwohl F nicht mehr da ist und somit kann auch der Schatz noch gefunden werden.
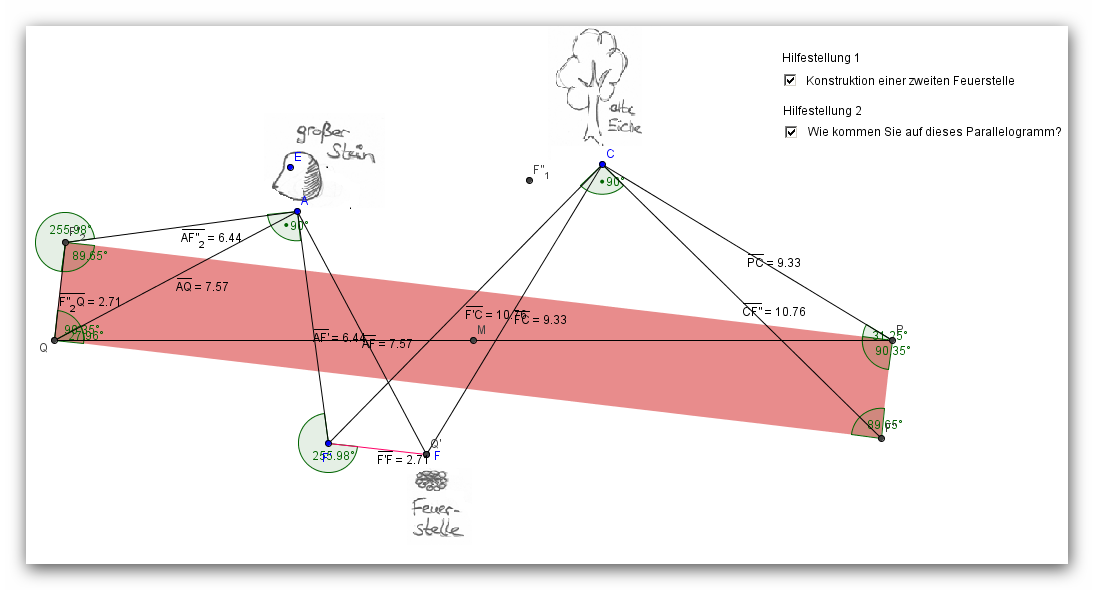 --RicRic
--RicRic
Okay, jetzt haben wie den Schatz gefunden, aber mit welcher speziellen Eigenschaft der Parallelogramme hat das jetzt zu tun? --RicRic 14:50, 8. Nov. 2011 (CET)
Super, dass du den Schatz gefunden hast!! Wirklich keine leichte Aufgabe.
Ich kann dir auch nicht sicher sagen, welche Eigenschaft des Parallelogramm hier direkt angesprochen wird. Ich vermute, dass man aus zwei zueinander parallelen Seiten, du zudem noch die selbe Länge haben, immer genau ein Parallelogramm konstruieren kann. - Ein Satz im Parallelogramm, der sich beweisen lässt.(Dieses benötigt man ja für das Abtragen des Winkels.)
Die ganze Aufgabe hat deshalb etwas mit dem Parallelogramm zu tun, da wie du richtig beschrieben hast, da zwei Drehungen um 90° durchgeführt werden. Gedreht wird die rote Strecke. Welches sind die Zentren der Drehungen? Zweimal eine Drehung um 90° entspricht einer Verschiebung, die durch das Parallelogramm verdeutlicht wird. --Tutorin Anne 14:55, 21. Nov. 2011 (CET)
Die Zentren der Drehung sind die Punke "Eiche" und "Stein", mit welcher speziellen Eigenschft symboliesiert das Parallelogramm die zwei Drehungen?--RicRic 21:00, 21. Nov. 2011 (CET)
mhh?--Tutorin Anne 16:33, 22. Nov. 2011 (CET)
Also heißt das, dass wenn ich eine Strecke um zwei belibige Punkte, welche den gleichen Abstand zu jedem Eckpunkt der Strecke haben, um je 90 Grand einmal mit der uhr und einmal gegen die Uhr drehe erhalte ich somit immer ein Parallelogramm!?--RicRic 21:30, 22. Nov. 2011 (CET)

