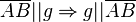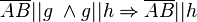Lösung von Aufgabe 5.5 (WS 11/12): Unterschied zwischen den Versionen
RicRic (Diskussion | Beiträge) |
|||
| (3 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 6: | Zeile 6: | ||
[[Category:Einführung_Geometrie]]<br /> | [[Category:Einführung_Geometrie]]<br /> | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
zu a) Punkt A steht genau dann in Relation zu Punkt B, wenn die Strecke <math>\overline{AB</math> keinen Schnittpunkt mit g hat. --[[Benutzer:Wookie|Wookie]] 12:18, 14. Nov. 2011 (CET)<br /> | zu a) Punkt A steht genau dann in Relation zu Punkt B, wenn die Strecke <math>\overline{AB</math> keinen Schnittpunkt mit g hat. --[[Benutzer:Wookie|Wookie]] 12:18, 14. Nov. 2011 (CET)<br /> | ||
| Zeile 19: | Zeile 14: | ||
Weitere Vorschläge zur Interpretation der Relation ...--[[Benutzer:Tutorin Anne|Tutorin Anne]] 19:33, 16. Nov. 2011 (CET) | Weitere Vorschläge zur Interpretation der Relation ...--[[Benutzer:Tutorin Anne|Tutorin Anne]] 19:33, 16. Nov. 2011 (CET) | ||
| − | Ein Punkt | + | Ein Punkt steht genau dann in Relation mit einem anderen Punkt, wenn er mit dem anderen Punkt auf der gleichen Halbebene liegt, wenn die Gerade g die Ebene in zwei Halbebenen teilt.<br /> |
| + | Ist reflexiv, da jeder Punkt auf der gleichen Halbebene liegt wie er selbst.<br /> | ||
| + | Ist symetrisch, da wenn A auf der einen Halbebene liegt und B auf der gleichen Halbebene liegt, dann liegt auch B auf der gleichen Halbebene wie A.<br /> | ||
| + | Ist transistiv, da wenn A und B auf der selben Halbebene liegen wie B und C, so liegen auch die Punke A und C auf der gleichen Halbebene--[[Benutzer:RicRic|RicRic]] 22:43, 16. Nov. 2011 (CET)<br /> | ||
| + | |||
| + | |||
| + | ==== Nicht korrekt==== | ||
| + | Vielleicht haben einige auch so gedacht und deshalb soll es hier mal stehen bleiben. --[[Benutzer:Andreas|Tutor Andreas]] 14:05, 19. Nov. 2011 (CET)<br /> | ||
| + | a)<s>parallel</s> --[[Benutzer:Todah raba|Todah raba]] 09:25, 15. Nov. 2011 (CET)<br /> | ||
| + | b) Die Relation hat folgende Eigenschaften: | ||
| + | <math>\ \Theta</math> ist reflexiv: <math>\overline{AB} || \overline{AB}</math> <br /> | ||
| + | <math>\ \Theta</math> ist symmetrisch: <math>\overline{AB} || g \Rightarrow g || \overline{AB}</math><br /> | ||
| + | <math>\ \Theta</math> ist transitiv: <math>\overline{AB} || g \ \wedge g || h \Rightarrow \overline{AB} || h</math><br /> | ||
| + | Also ist es eine Äquivalenzrelation. --[[Benutzer:Todah raba|Todah raba]] 17:02, 13. Nov. 2011 (CET)<br /> | ||
| + | * Es wäre gut, wenn der Autor diesen Kommentar verbessern würde. --[[Benutzer:Andreas|Tutor Andreas]] 11:18, 17. Nov. 2011 (CET) | ||
| + | * Ich stimme der Lösung von RicRic zu, ich hatte bei meiner Lösung eine falsche Interpretation der Relation angenommen. <br /> | ||
| + | Soll ich den Beitrag löschen? <br />--[[Benutzer:Todah raba|Todah raba]] 16:47, 17. Nov. 2011 (CET)<br /> | ||
| + | * Wenn du ihn nicht verbessern willst und erkannt hast, dass es so nicht stimmt, dann sollte man ihn zumindest als | ||
| + | "nicht korrekt" markieren. | ||
Aktuelle Version vom 19. November 2011, 14:05 Uhr
Es seien eine Ebene E (aufgefasst als Punktmenge) und eine Gerade g in E gegeben. Wir betrachten folgende Relation  (
( ist ein willkürlich gewähltes Symbol, um die Relation nicht mit dem unauffälligen Buchstaben R bezeichnen zu müssen) in der Menge
ist ein willkürlich gewähltes Symbol, um die Relation nicht mit dem unauffälligen Buchstaben R bezeichnen zu müssen) in der Menge 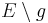 (also alle Punkte der Ebene E, die nicht der Geraden g angehören): Für beliebige
(also alle Punkte der Ebene E, die nicht der Geraden g angehören): Für beliebige 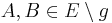 gilt:
gilt: 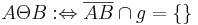 .
.
a) Beschreiben Sie die Relation  verbal und veranschaulichen Sie diese Relation.
verbal und veranschaulichen Sie diese Relation.
b) Begründen Sie anschaulich, dass  eine Äquivalenzrelation ist. Formulieren Sie dazu die Eigenschaften von Äquivalenzrelationen konkret auf die Relation
eine Äquivalenzrelation ist. Formulieren Sie dazu die Eigenschaften von Äquivalenzrelationen konkret auf die Relation  bezogen.
bezogen.
Hinweis: Sie können die Transitivität noch nicht exakt beweisen; in dieser Aufgabe geht es zunächst darum, die Relationseigenschaften als geometrische Eigenschaften zu interpretieren und zu verstehen.
zu a) Punkt A steht genau dann in Relation zu Punkt B, wenn die Strecke Fehler beim Parsen(Syntaxfehler): \overline{AB
keinen Schnittpunkt mit g hat. --Wookie 12:18, 14. Nov. 2011 (CET)
zu b) begründest du mit der Parallelität? Warum? Steht doch nichts, davon in der Relation?--Anna S 22:13, 14. Nov. 2011 (CET)
@ Anna S: Du hast recht, das war wohl ein Denkfehler. Die Relation beschreibt nicht Parallelität, sondern, "Element der selben Gerade wie". --Todah raba 09:25, 15. Nov. 2011 (CET)
@ Todah raba: Was meinst du mit "Element der selben Gerade wie" ? Gibt es durch zwei Punkte nicht immer ein Gerade?
Weitere Vorschläge zur Interpretation der Relation ...--Tutorin Anne 19:33, 16. Nov. 2011 (CET)
Ein Punkt steht genau dann in Relation mit einem anderen Punkt, wenn er mit dem anderen Punkt auf der gleichen Halbebene liegt, wenn die Gerade g die Ebene in zwei Halbebenen teilt.
Ist reflexiv, da jeder Punkt auf der gleichen Halbebene liegt wie er selbst.
Ist symetrisch, da wenn A auf der einen Halbebene liegt und B auf der gleichen Halbebene liegt, dann liegt auch B auf der gleichen Halbebene wie A.
Ist transistiv, da wenn A und B auf der selben Halbebene liegen wie B und C, so liegen auch die Punke A und C auf der gleichen Halbebene--RicRic 22:43, 16. Nov. 2011 (CET)
Nicht korrekt
Vielleicht haben einige auch so gedacht und deshalb soll es hier mal stehen bleiben. --Tutor Andreas 14:05, 19. Nov. 2011 (CET)
a)parallel--Todah raba 09:25, 15. Nov. 2011 (CET)
b) Die Relation hat folgende Eigenschaften:ist reflexiv:
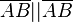
ist symmetrisch:
ist transitiv:
Also ist es eine Äquivalenzrelation. --Todah raba 17:02, 13. Nov. 2011 (CET)
* Es wäre gut, wenn der Autor diesen Kommentar verbessern würde. --Tutor Andreas 11:18, 17. Nov. 2011 (CET) * Ich stimme der Lösung von RicRic zu, ich hatte bei meiner Lösung eine falsche Interpretation der Relation angenommen.
Soll ich den Beitrag löschen?
--Todah raba 16:47, 17. Nov. 2011 (CET)
* Wenn du ihn nicht verbessern willst und erkannt hast, dass es so nicht stimmt, dann sollte man ihn zumindest als "nicht korrekt" markieren.