Lösung von Aufg. 11.3 (WS 11/12): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
RicRic (Diskussion | Beiträge) |
RicRic (Diskussion | Beiträge) |
||
| Zeile 1: | Zeile 1: | ||
Beweisen Sie: Zu jedem Winkel gibt es genau eine Winkelhalbierende. | Beweisen Sie: Zu jedem Winkel gibt es genau eine Winkelhalbierende. | ||
| − | Vorr.: <math>\angle | + | Vorr.: <math>\angle ASB</math> ; Betrachte nur eine Ebene<br /> |
Beh.: <math>\exists ! \ SW^{+} \wedge |\angle ASW| = |\angle BSW|</math><br /> | Beh.: <math>\exists ! \ SW^{+} \wedge |\angle ASW| = |\angle BSW|</math><br /> | ||
Beweis: | Beweis: | ||
| Zeile 12: | Zeile 12: | ||
| (2)<math>\exists y: y=\frac{1} {2} x</math> || Rechnen in R, (1) | | (2)<math>\exists y: y=\frac{1} {2} x</math> || Rechnen in R, (1) | ||
|- | |- | ||
| − | | (3)<math>\exists \angle ASW: |\angle ASW|=y</math> || Winkelkonstruktionaxiom, (2) | + | | (3)<math>\exists \angle ASW: |\angle ASW|=y</math> <math>\wedge W\in \ SB,A^{+}</math> --[[Benutzer:RicRic|RicRic]] 14:26, 5. Jan. 2012 (CET)|| Winkelkonstruktionaxiom, (2) |
|- | |- | ||
| (4)<math>\exists! \ SW^{+}</math> || Winkelkonstruktionaxiom, (3) Existiert und ist eindeutig laut Axiom "genau ein Strahl" | | (4)<math>\exists! \ SW^{+}</math> || Winkelkonstruktionaxiom, (3) Existiert und ist eindeutig laut Axiom "genau ein Strahl" | ||
Version vom 5. Januar 2012, 14:26 Uhr
Beweisen Sie: Zu jedem Winkel gibt es genau eine Winkelhalbierende.
Vorr.: 
; Betrachte nur eine Ebene
Beh.: 
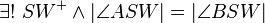
Beweis:
| Schritt | Begründung |
|---|---|
(1) |
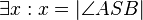Winkelmaßaxiom |
(2) |
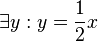Rechnen in R, (1) |
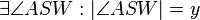(3) 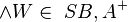 --RicRic 14:26, 5. Jan. 2012 (CET) |
Winkelkonstruktionaxiom, (2) |
(4) |
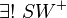Winkelkonstruktionaxiom, (3) Existiert und ist eindeutig laut Axiom "genau ein Strahl" |
(5)  |
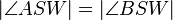(2),(3), Winkeladditonsaxiom |
-- Ich glaube um das Winkelkonstruktionsaxiom verwenden zu können, musst du erst noch die Halbebene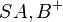 
bestimmen. --Wookie 10:53, 4. Jan. 2012 (CET)
-- Du meinst sonnst hätte ich zwei Möglichkeiten um den Strahl anzutragen. Stimmt, ist die Frage ob es einen Unterschied macht, da der Betrag gleich ist, komme dann eben bei B' an.
