Lösung von Aufg. 11.3 (WS 11/12)
Beweisen Sie: Zu jedem Winkel gibt es genau eine Winkelhalbierende.
Vorr.:  ; Betrachte nur eine Ebene
; Betrachte nur eine Ebene
Beh.: 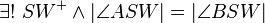
Beweis:
| Schritt | Begründung |
|---|---|
(1)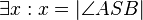 |
Winkelmaßaxiom |
(2)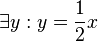 |
Rechnen in R, (1) |
(3)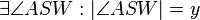 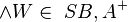 --RicRic 14:26, 5. Jan. 2012 (CET) --RicRic 14:26, 5. Jan. 2012 (CET) |
Winkelkonstruktionaxiom, (2) |
(4)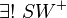 |
Winkelkonstruktionaxiom, (3) Existiert und ist eindeutig laut Axiom "genau ein Strahl" |
(5) 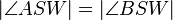 |
(2),(3), Winkeladditonsaxiom |
-- Ich glaube um das Winkelkonstruktionsaxiom verwenden zu können, musst du erst noch die Halbebene 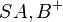 bestimmen. --Wookie 10:53, 4. Jan. 2012 (CET)
bestimmen. --Wookie 10:53, 4. Jan. 2012 (CET)
-- Du meinst sonnst hätte ich zwei Möglichkeiten um den Strahl anzutragen. Stimmt, ist die Frage ob es einen Unterschied macht, da der Betrag gleich ist, komme dann eben bei B' an.
- Woher wissen Sie, dass W im Innern des Winkels
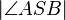 liegt? Nur dann können Sie nämlich das Winkeladditionsaxiom anwenden! --Spannagel 09:08, 9. Jan. 2012 (CET)
liegt? Nur dann können Sie nämlich das Winkeladditionsaxiom anwenden! --Spannagel 09:08, 9. Jan. 2012 (CET)
- Muss ich also in Schritt (3) noch zusätzlich sagen:
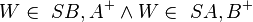 ?= --RicRic 19:36, 9. Jan. 2012 (CET)
?= --RicRic 19:36, 9. Jan. 2012 (CET)
- Ja, dass muss man nennen. Allerdings kannst du das nicht einfach so sagen. Woher willst du wissen, ob es gilt?--Tutorin Anne 11:35, 11. Jan. 2012 (CET)
Okay dann füge ich hier noch einen Schritt ein:
| Überschrift 1 | Überschrift 2 |
|---|---|
(3)Fall 1: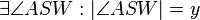 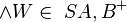 |
Winkelkonstruktionaxiom, (2) |
(3,5)Fall 2: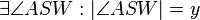 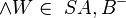 |
Winkelkonstruktionaxiom, (2)ist nicht weiter zu berachen, da nicht im inneren von 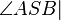 und somit laut der Def. nicht die Winkelhalbierende. und somit laut der Def. nicht die Winkelhalbierende.
|
Betrache hier den Strahl SA+, da auf diesen Stahl nach dem entsprechenden Betrag der Winekel konstuiert wird, es gibt nur diese beiden Möglichkeiten und eine lässt ich laut der Definition der Winkelhalbierenen leicht ausschließen. Habe ich jetzt die Existenz und Eindeutigkeit gezeigt?--RicRic 20:43, 11. Jan. 2012 (CET)

