Lösung von Aufg. 11.3 (WS 11/12): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
RicRic (Diskussion | Beiträge) |
|||
| Zeile 23: | Zeile 23: | ||
: Woher wissen Sie, dass W im Innern des Winkels <math>|\angle ASB|</math> liegt? Nur dann können Sie nämlich das Winkeladditionsaxiom anwenden! --[[Benutzer:Spannagel|Spannagel]] 09:08, 9. Jan. 2012 (CET) | : Woher wissen Sie, dass W im Innern des Winkels <math>|\angle ASB|</math> liegt? Nur dann können Sie nämlich das Winkeladditionsaxiom anwenden! --[[Benutzer:Spannagel|Spannagel]] 09:08, 9. Jan. 2012 (CET) | ||
| − | + | : Muss ich also in Schritt (3) noch zusätzlich sagen: <math> W\in \ SB,A^{+} \wedge W\in \ SA,B^{+}</math> ?= --[[Benutzer:RicRic|RicRic]] 19:36, 9. Jan. 2012 (CET) | |
[[Kategorie:Einführung_Geometrie]] | [[Kategorie:Einführung_Geometrie]] | ||
Version vom 9. Januar 2012, 19:36 Uhr
Beweisen Sie: Zu jedem Winkel gibt es genau eine Winkelhalbierende.
Vorr.: 
; Betrachte nur eine Ebene
Beh.: 
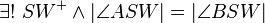
Beweis:
| Schritt | Begründung |
|---|---|
(1) |
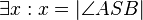Winkelmaßaxiom |
(2) |
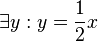Rechnen in R, (1) |
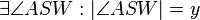(3) 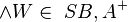 --RicRic 14:26, 5. Jan. 2012 (CET) |
Winkelkonstruktionaxiom, (2) |
(4) |
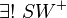Winkelkonstruktionaxiom, (3) Existiert und ist eindeutig laut Axiom "genau ein Strahl" |
(5)  |
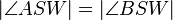(2),(3), Winkeladditonsaxiom |
-- Ich glaube um das Winkelkonstruktionsaxiom verwenden zu können, musst du erst noch die Halbebene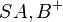 
bestimmen. --Wookie 10:53, 4. Jan. 2012 (CET)
-- Du meinst sonnst hätte ich zwei Möglichkeiten um den Strahl anzutragen. Stimmt, ist die Frage ob es einen Unterschied macht, da der Betrag gleich ist, komme dann eben bei B' an.
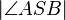liegt? Nur dann können Sie nämlich das Winkeladditionsaxiom anwenden! --
?= --
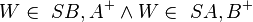