Übung 7: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Aufgabe 7.10) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 7.9) |
||
| Zeile 47: | Zeile 47: | ||
[[Lösung von Aufgabe 7.9]] | [[Lösung von Aufgabe 7.9]] | ||
| + | |||
| + | == Aufgabe 7.10 == | ||
| + | Beweisen Sie: Jede Strecke hat höchstens einen Mittelpunkt. | ||
| + | |||
| + | [[Lösung von Aufgabe 7.10]] | ||
Aktuelle Version vom 3. Juni 2010, 23:05 Uhr
Inhaltsverzeichnis |
Aufgabe 7.1
Beweisen Sie: Zu jeder Strecke 
existiert genau eine Strecke 
mit 
und 
.
Aufgabe 7.2
Beweisen Sie: Zu jeder Strecke existiert genau eine Strecke mit 
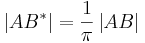und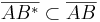 
.
Aufgabe 7.3
Der Punkt 
möge die Strecke 
derart in die Teilstrecken und 
teilen, dass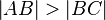 
gilt. Beweisen Sie:
Wenn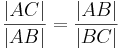 
, dann 
.
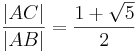Aufgabe 7.4
Definieren noch einmal die Begriffe Halbgerade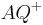 
und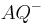 
. In diesen neuen Definitionen dürfen Sie die Zwischenrelation nicht explizit verwenden. Beweisen Sie dann, dass Ihre neuen Definitionen zur | Definition II.3 äquivalent sind.
Aufgabe 7.5
Beweisen Sie: Der Durchschnitt zweier konvexer Punktmengen ist konvex.
Aufgabe 7.6
Formulieren Sie die Kontraposition der Implikation aus Aufgabe 7.5.
Aufgabe 7.7
Zeigen Sie mittels einer Skizze, dass die Umkehrung der Implikation aus Aufgabe 7.5 nicht wahr ist.
Aufgabe 7.8
Unter einem Dreieck versteht man die Vereinigungsmenge von drei besonderen Strecken (umgangssprachlich: Das Dreieck ist sein Rand.). Definieren Sie den Begriff Dreieck 
.
Aufgabe 7.9
Definieren Sie mittels des Schnitts geeigneter Halbebenen den Begriff des Inneren eines Dreiecks .
Aufgabe 7.10
Beweisen Sie: Jede Strecke hat höchstens einen Mittelpunkt.
