Lösung von Aufgabe 11.5P (SoSe 12): Unterschied zwischen den Versionen
| Zeile 14: | Zeile 14: | ||
Du kommst auf den richtigen Punkt G. Allerdings kannst du die Schritte selbst nicht ganz begründen. G kann auch anders konstruiert werden.<br /> | Du kommst auf den richtigen Punkt G. Allerdings kannst du die Schritte selbst nicht ganz begründen. G kann auch anders konstruiert werden.<br /> | ||
Denkt hier daran, dass eine Drehung eine Verkettung zweier Geradenspiegelungen, die sich schneiden ist und eine Verschiebung, eine Verkettung zweier paralleler Geradenspiegelungen. Zeichnet diese ein und schiebt sie so ineinander, dass ihr möglichst einige Spiegelungen reduzieren könnt.--[[Benutzer:Tutorin Anne|Tutorin Anne]] 20:21, 5. Jul. 2012 (CEST)<br /><br /> | Denkt hier daran, dass eine Drehung eine Verkettung zweier Geradenspiegelungen, die sich schneiden ist und eine Verschiebung, eine Verkettung zweier paralleler Geradenspiegelungen. Zeichnet diese ein und schiebt sie so ineinander, dass ihr möglichst einige Spiegelungen reduzieren könnt.--[[Benutzer:Tutorin Anne|Tutorin Anne]] 20:21, 5. Jul. 2012 (CEST)<br /><br /> | ||
| − | ich finde meine konstruktion okay - immerhin muss ich nicht zwei spiegelachsen übereinander schieben. ;-)<br /> | + | ich finde meine konstruktion okay - ich habe es mir viel leichter gemacht und immerhin muss ich nicht zwei spiegelachsen übereinander schieben. ;-)<br /> |
ich weiss nur nicht, wie ich sie hier schriftlich erklären soll...<br /> | ich weiss nur nicht, wie ich sie hier schriftlich erklären soll...<br /> | ||
vielleicht kann es jemand nachvollziehen und die begründung nachreichen?--[[Benutzer:Studentin|Studentin]] 22:46, 9. Jul. 2012 (CEST) | vielleicht kann es jemand nachvollziehen und die begründung nachreichen?--[[Benutzer:Studentin|Studentin]] 22:46, 9. Jul. 2012 (CEST) | ||
[[Kategorie:Einführung_P]] | [[Kategorie:Einführung_P]] | ||
Version vom 9. Juli 2012, 21:46 Uhr
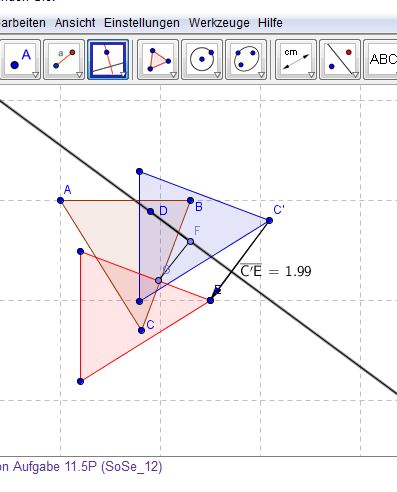
Das Dreieck 
wird an Punkt D um 90 gedreht. Das gedrehte Dreieck wird nun um den eingezeichneten Vektor verschoben. Gibt es einen Punkt der Ebene, der nun genau wieder an seinem ursprünglichen Ort liegt? Konstruieren Sie ggf. diesen Punkt und begründen Sie!
Punkt g,
meine konstruktion:
1. eine senkrechte zum verktor durch den punkt d.
2. punkt f: halbe vektorlänge vom punkt d abgetragen
3. senkrechte zu df durch den punkt f
4. halbe vektorlänge abgetragen --> punkt g
begründung:
1. der gesuchte punkt muss durch die drehung an genau den punkt kommen, der genau gegenläufig dem vektor liegt (ich weiß nicht, wie man dies nennt), d.h. der punkt g und der punkt g' liegen parallel zum vektor und der abstand von g zu g' entspricht der vektorlänge.
2. genaue lage des punktes g: kann ich nicht wirklich begründen; ich habe mir ein quadrat vorgestellt, g ung g' sind zwei ecken des quadrates und die diagonalen des quadrates schneiden sich in d. daher sind sowohl der abstand zwischen d und f als auch zwischen f und g die halbe vektorlänge)
--Studentin 22:31, 1. Jul. 2012 (CEST)
Du kommst auf den richtigen Punkt G. Allerdings kannst du die Schritte selbst nicht ganz begründen. G kann auch anders konstruiert werden.
Denkt hier daran, dass eine Drehung eine Verkettung zweier Geradenspiegelungen, die sich schneiden ist und eine Verschiebung, eine Verkettung zweier paralleler Geradenspiegelungen. Zeichnet diese ein und schiebt sie so ineinander, dass ihr möglichst einige Spiegelungen reduzieren könnt.--Tutorin Anne 20:21, 5. Jul. 2012 (CEST)
ich finde meine konstruktion okay - ich habe es mir viel leichter gemacht und immerhin muss ich nicht zwei spiegelachsen übereinander schieben. ;-)
ich weiss nur nicht, wie ich sie hier schriftlich erklären soll...
vielleicht kann es jemand nachvollziehen und die begründung nachreichen?--Studentin 22:46, 9. Jul. 2012 (CEST)
