Lösung von Aufgabe 11.5P (SoSe 12)
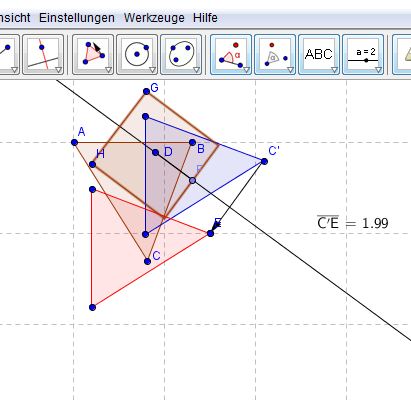
Das Dreieck  wird an Punkt D um 90 gedreht. Das gedrehte Dreieck wird nun um den eingezeichneten Vektor verschoben. Gibt es einen Punkt der Ebene, der nun genau wieder an seinem ursprünglichen Ort liegt? Konstruieren Sie ggf. diesen Punkt und begründen Sie!
wird an Punkt D um 90 gedreht. Das gedrehte Dreieck wird nun um den eingezeichneten Vektor verschoben. Gibt es einen Punkt der Ebene, der nun genau wieder an seinem ursprünglichen Ort liegt? Konstruieren Sie ggf. diesen Punkt und begründen Sie!
Punkt g,
meine konstruktion:
1. eine senkrechte zum verktor durch den punkt d.
2. punkt f: halbe vektorlänge vom punkt d abgetragen
3. senkrechte zu df durch den punkt f
4. halbe vektorlänge abgetragen --> punkt g
begründung:
1. der gesuchte punkt muss durch die drehung an genau den punkt kommen, der genau gegenläufig dem vektor liegt (ich weiß nicht, wie man dies nennt), d.h. der punkt g und der punkt g' liegen parallel zum vektor und der abstand von g zu g' entspricht der vektorlänge.
2. genaue lage des punktes g: kann ich nicht wirklich begründen; ich habe mir ein quadrat vorgestellt, g ung g' sind zwei ecken des quadrates und die diagonalen des quadrates schneiden sich in d. daher sind sowohl der abstand zwischen d und f als auch zwischen f und g die halbe vektorlänge)
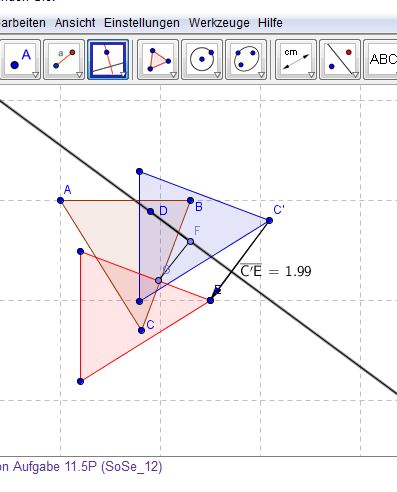
Du kommst auf den richtigen Punkt G. Allerdings kannst du die Schritte selbst nicht ganz begründen. G kann auch anders konstruiert werden.
Denkt hier daran, dass eine Drehung eine Verkettung zweier Geradenspiegelungen, die sich schneiden ist und eine Verschiebung, eine Verkettung zweier paralleler Geradenspiegelungen. Zeichnet diese ein und schiebt sie so ineinander, dass ihr möglichst einige Spiegelungen reduzieren könnt.--Tutorin Anne 20:21, 5. Jul. 2012 (CEST)
ich finde meine konstruktion okay - ich habe es mir viel leichter gemacht und immerhin muss ich nicht zwei spiegelachsen übereinander schieben. ;-)
ich weiss nur nicht, wie ich sie hier schriftlich erklären soll...
vielleicht kann es jemand nachvollziehen und die begründung nachreichen?--Studentin 22:46, 9. Jul. 2012 (CEST)
45 minuten später versuche ich es selöbst noch einmal, ich habe das quadrat eingezeichnet:
wenn ich weiss, dass der gesuchte punkt (p) bei einer drehung um 90° so ankommen muss (p'), dass er bei der anschließenden verschiebung (p´´) um den vektor wieder bei seinem ursprungspunkt (p) landet, weiß ich ja, dass die punkte p und p' irgendwo parallel zum vektor liegen müssen und der abstand beider punkte der vektorlänge entsprechen muss.
gleichzeitig weiß ich ja, dass der abstand zwischen punkt p und d gleich groß dem abstand des punktes p' zu d sein muss. (drehung)
der winkel pdd' soll 90° betragen. also habe ich ein dreieck dpp' mit pp' dem gleichen abstand entsprechend der vektorlänge und dem abstand d zu f (mittelpunkt der strecke pp') mit der halben vektorlänge.
... ich merke selbst, dass ich es wohl am bild mündlich erklären müsste...
--Studentin 23:31, 9. Jul. 2012 (CEST)
- Danke für die ausführliche Erklärung und Begründung deiner Konstruktion. Ich kann diese nachvollziehen und würde sagen, sie ist korrekt. Es gibt auch die Möglichkeit über Achsenverschiebung zu argumentieren, dann kann man sich auch gleich auf Aufgabe 11.4 beziehen - falls man diese mit Achsenverschiebungen begründet hat.--Tutorin Anne 09:17, 10. Jul. 2012 (CEST)
Hi, da ich irgendwie noch nicht ganz verstanden habe, wie man Dateien von geogebra hier einspeichert, schreibe ich kurz die Lösung. Wir haben die Drehung Sa°Sb und die zwei parallelen Achsenspiegelungen Sc°Sd, wobei deren Abstand = der Vektorlänge ist. Jetzt kann ich - wie bei Aufgabe 11.4 gezeigt - bei einer Verkettung dieser Spiegelungen die Spiegelachsen so drehen bzw. die Parallelen so verschieben, dass Sa°Sc`identisch sind und wegfallen. Es bleibt die Verkettung Sb°Sd` übrig. Mathemtischer betrachtet sieht das so aus: (Sa°Sb)°(Sc°Sd)=(Sa°Sc`)[wobei diese id. sind und wegfallen werden]°(Sb°Sd`)=Sb°Sd`, mit Winkel (b,S2,d`)=45° und |ad`|=Vektorlänge. D.H. Jener Punkt des Dreiecks ABC wird bei der ingesamten Ausführung wieder auf sich selbst abgebildet, der durch den "zweiten Drehpunkt S2" geht, weil dieser Punkt der einzige Punkt ist, der bei der Verkettung von Sb°Sd` Fixpunkt ist. Schnitzel 12:01, 13. Jul. 2012 (CEST)
So sehe ich das auch!
Allerding müsste der Abstand |Sc°Sd| (kann man das so überhaupt schreiben??) die halbe Vektorlänge sein da bei einer Verschiebund um den doppelten Abstand zwischen den beiden Spiegelachsen verschoben wird. Sprich der Voktor ist doppelt so lang wie der Abstand zwischen Sc und Sd.
--Jussuf Ölkan 17:17, 13. Jul. 2012 (CEST)
Jo, stimmt, du hast Recht. Die Vektorlänge beschreibt ja die Länge zwischen zwei Punkten (wie man bei "Studentin" gut sehen kann). Deshalb muss der Abstand zwischen den beiden parallen Spiegelachsen die Hälfte des Vektors betragen, damit das mit dem Urpunkt und dem Bildpunkt hinhaut. Vielen Dank :) Schnitzel 20:28, 13. Jul. 2012 (CEST)
- Sehr guter Austausch! Besser als die Bewegung in Betragsstriche zu schreiben ist : d(c,d) (Abstand der Geraden) =1/2 Vekorlänge.
- Wichtig ist noch, dass Verkettung von Abbildungen nicht kommutativ ist, d.h. die Reihenfolge der Durchführung ist wichtig.(Siehe Zusatzaufgaben 10.1 Lösung von Zusatzaufgabe 10.1P (SoSe_12)). Es ist also entscheident, dass Gerade b und c aufeinandergedreht werden und nicht a und c! (Ausnahme: Kommutativ ist nur die Punktspiegelung).--Tutorin Anne 13:58, 16. Jul. 2012 (CEST)
ich hab es mal für's wiki konstruiert:
die obere der beiden parallelen geraden ist sowohl spiegelachse bei der verschiebung als auch spiegelachse bei der drehung.
da an dieser achse daher zwei mal gespiegelt wird (einmal hin und dann gleich wieder zurück) kann man's auch gleich bleiben lassen, diese gerade außer acht lassen und nur noch an den anderen zwei verbleibenden achsen spiegeln.
punkt i (schnittpunkt der beiden verbliebenen achsen) ist "neuer" drehpunkt und gleichzeitig fixpunkt und daher unser gesuchter punkt:
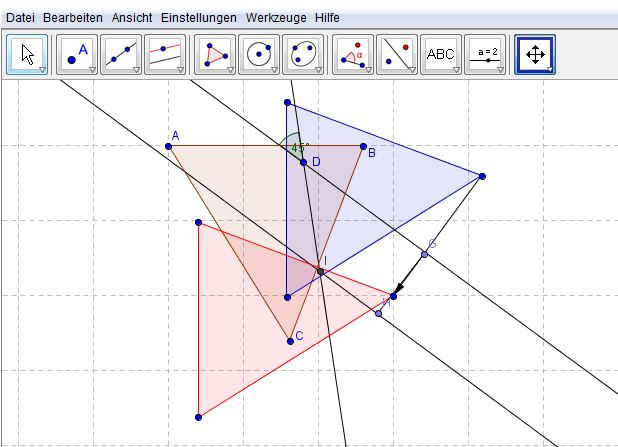
--Studentin 21:00, 13. Jul. 2012 (CEST)