Diskussion:Lösung von Aufgabe 11.5P (SoSe 12)

Punkt g,
meine konstruktion:
1. eine senkrechte zum verktor durch den punkt d.
2. punkt f: halbe vektorlänge vom punkt d abgetragen
3. senkrechte zu df durch den punkt f 4. halbe vektorlänge abgetragen --> punkt g

begründung:
1. der gesuchte punkt muss durch die drehung an genau den punkt kommen, der genau gegenläufig dem vektor liegt (ich weiß nicht, wie man dies nennt), d.h. der punkt g und der punkt g' liegen parallel zum vektor und der abstand von g zu g' entspricht der vektorlänge.
2. genaue lage des punktes g: kann ich nicht wirklich begründen; ich habe mir ein quadrat vorgestellt, g ung g' sind zwei ecken des quadrates und die diagonalen des quadrates schneiden sich in d. daher sind sowohl der abstand zwischen d und f als auch zwischen f und g die halbe vektorlänge)

--Studentin 22:31, 1. Jul. 2012 (CEST)

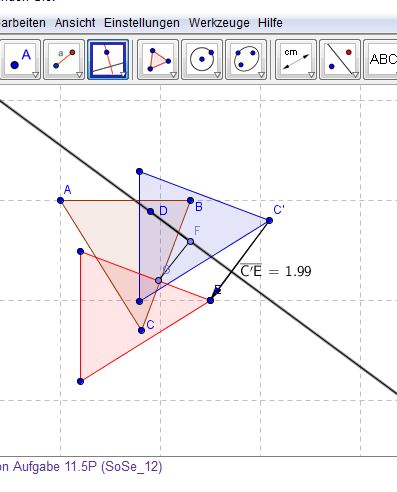
Du kommst auf den richtigen Punkt G. Allerdings kannst du die Schritte selbst nicht ganz begründen. G kann auch anders konstruiert werden.
Denkt hier daran, dass eine Drehung eine Verkettung zweier Geradenspiegelungen, die sich schneiden ist und eine Verschiebung, eine Verkettung zweier paralleler Geradenspiegelungen. Zeichnet diese ein und schiebt sie so ineinander, dass ihr möglichst einige Spiegelungen reduzieren könnt.--Tutorin Anne 20:21, 5. Jul. 2012 (CEST)

Ich bin leider nicht/noch nicht fähig meine Konstruktion hochzuladen... 1. Die beiden Spiegelachsen der Verschiebung haben den Abstand des halben Vektors zueinander.(Eigenschaft Verschiebung) Diese beiden Spiegelachsen so verschieben, dass a' durch den Drehpunkt D geht und b' durch den Punkt der an seinem ursprünglichen Ort bleibt.(Letzteres kann man natürlich vorher noch nicht wissen, ist dann aber anschaulicher...) 2. Die beiden Spiegelachsen der Drehung (45°) bei gleichbleibendem Winkel und festem D so drehen, dass c' parallel zu den Geraden der Verschiebung ist, bzw. c' und a' identisch sind. 3.c' und a' fallen raus da sie identisch sind und der neue Drehpunkt D' befindet sich am Schnittpunkt von b' und d'. 4.D' ist Fixpunkt und Punkt des Ursprungsdreiecks. Deshalb bleibt er an seinem ursprünglichen Ort. --Jussuf Ölkan 22:45, 12. Jul. 2012 (CEST)