Serie 5 (WS 12 13): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(→‎Aufgabe 5.2)
(→‎Aufgaben zum Abstand)
Zeile 1: Zeile 1:
−
=Aufgaben zum Abstand=
+
=weitere Aufgaben zur Inzidenz=
  
 
==Aufgabe 5.1==
 
==Aufgabe 5.1==
−
<u>'''Satz:'''</u>
+
Begründen Sie:
−
::Es seien <math>A,B</math> und <math>C</math> drei paarweise verschiedene Punkte.<br />
+
#Jedes Modell für die Inzidenzaxiome der Ebene beinhaltet wenigstens 3 paarweise verschiedene Punkte.
−
::Wenn der Punkt <math>B</math> zwischen den Punkten <math>A</math> und <math>C</math> liegt, dann liegt weder <math>A</math> zwischen <math>B</math> und <math>C</math> noch <math>C</math> zwischen <math>A</math> und <math>B</math>.
+
#Jedes Modell für die Inzidenzaxiome des Raumes beinhaltet wenigstens 3 paarweise verschiedene Punkte.
−
Beweisen Sie diesen Satz.
+
−
 
+
 
<br />
 
<br />
 
[[Lösung von Aufgabe 5.1_S (WS_12_13)]]
 
[[Lösung von Aufgabe 5.1_S (WS_12_13)]]

Version vom 24. November 2012, 13:38 Uhr

Inhaltsverzeichnis

weitere Aufgaben zur Inzidenz

Aufgabe 5.1

Begründen Sie:

  1. Jedes Modell für die Inzidenzaxiome der Ebene beinhaltet wenigstens 3 paarweise verschiedene Punkte.
  2. Jedes Modell für die Inzidenzaxiome des Raumes beinhaltet wenigstens 3 paarweise verschiedene Punkte.


Lösung von Aufgabe 5.1_S (WS_12_13)

Aufgabe 5.2

Es seien A, B, C und D vier paarweise verschiedene Punkte.
Beweisen Sie:
Fehler beim Parsen(Syntaxfehler): \overline{CD} \subset \overline{AB} \Rightarrow \forall P \in \overline{CD}: \operatorname{Zw}(APB} .




Lösung von Aufgabe 5.2_S (WS_12_13)

Aufgabe 5.3

Zeigen Sie, dass für drei paarweise verschiedene Punkte \ A, B und \ C gilt:
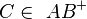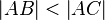Wenn C \in \ AB^{+} und \left| AB \right| < \left| AC \right| dann gilt \operatorname Zw (A, B, C)


Lösung von Aufgabe 5.3_S (WS_12_13)


Aufgabe 5.4

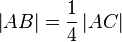Beweisen Sie: Zu jeder Strecke \overline{AB} existiert genau eine Strecke \overline{AC} auf \ AB^{+} mit \left| AB \right| = \frac{1}{4} \left| AC \right| und \overline{AB} \subset \overline{AC}



Lösung von Aufgabe 5.4_S (WS_12_13)

Weitere Aufgabe zur Inzidenz

Aufgabe 5.5

Beweisen Sie: Je vier nicht komplanare Punkte sind paarweise verschieden (Hinweis: Nutzen Sie bei der Beweisführung die Sätze aus Aufgabe 4.3 und Zusatzaufgabe 4.4).

Lösung von Aufg. 5.5_S (WS_12_13)

Von „http://geometrie.zum.de/index.php?title=Serie_5_(WS_12_13)&oldid=18923“