Serie 2 SoSe 2013: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Aufgabe 2.04 SoSe 2013) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 2.04 SoSe 2013) |
||
| Zeile 34: | Zeile 34: | ||
=Aufgabe 2.04 SoSe 2013= | =Aufgabe 2.04 SoSe 2013= | ||
Sie haben einen Klassensatz Heidelberger Winkelkreuze ([[Heidelberger_Winkelkreuz]]). | Sie haben einen Klassensatz Heidelberger Winkelkreuze ([[Heidelberger_Winkelkreuz]]). | ||
| − | + | Mit dem Heidelberger Winkelkreuz lassen Sie Ihre Schüler nur Parallelogramme spannen. Danach sollen eine Regel entwickeln, welche Stifte auf den Schenkeln des Kreuzes auszuwählen sind, damit ein Parallelogramm gespannt wird. | |
| − | + | # Wie könnte diese Regel formuliert sein? | |
| + | # Formulieren Sie eine Definition des Begriffs Parallelogramm, der sich unmittelbar aus dieser Regel ergibt. | ||
| + | [[Lösung von Aufgabe 2.04 SoSe 2013 S]] | ||
| + | =Aufgabe 2.05 SoSe 2013= | ||
Version vom 27. April 2013, 11:53 Uhr
Inhaltsverzeichnis |
Die gesamte Serie zum Ausdrucken
Aufgabe 2.01 SoSe 2013
Ergänzen Sie die Lücken durch Verwendung von
- notwendig aber nicht hinreichend
- hinreichend aber nicht notwendig
- hinreichend
- notwenig
- notwendig und hinreichend.
Sollten mehrere diesbezügliche Auswahlmöglichkeiten bestehen, verwenden Sie die schärfste der möglichen Formulierungen.
- Dafür, dass
die Summe 
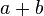teilt, ist es ... , dass sowohl 
als auch
teilt. (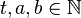
)
- Dafür, dass
ein Rechteck ist, ist es ... , dass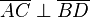 
gilt.
- Dafür, dass ein Dreieck
rechtwinklig ist, ist es ... , dass kein Innenwinkel von größer als 90° ist.
- Dafür, dass ein Dreieck stumpfwinklig ist, ist es ... , dass ein Innenwinkel von größer als 90° ist.
- Dafür, dass ein Dreieck rechtwinklig ist, ist es ... , dass der Mittelpunkt seines Umkreises der Mittelpunkt einer seiner Seiten ist.
- Dafür dass ein Viereck ein Rechteck ist, ist es ... , dass alle seine Seiten gleichlang sind.
- Dafür dass ein Viereck ein Rechteck ist, ist es ... , dass es einen rechten Innenwinkel hat und alle seine Seiten gleichlang sind.
Lösung von Aufgabe 2.02 SoSe 2013 S
Aufgabe 2.02 SoSe 2013
Unter einem Trapez wollen wir ein Viereck verstehe, das ein Paar zueinender paralleler Seiten hat. Es sei ein Trapez. Formulieren Sie
- eine zwar hinreichende aber nicht notwendige Bedingung dafür, dass
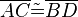gilt,
- eine hinreichende und notwendige Bedingung dafür, dass 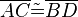gilt,
- eine notwendige aber nicht hinreichende Bedingung dafür, dass 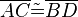gilt,
- ein Kriterium dafür, dass 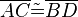gilt.
Lösung von Aufgabe 2.02 SoSe 2013 S
Aufgabe 2.03 SoSe 2013
Definieren Sie den Begriff Parallelogramm
- nur unter Verwendung der Eigenschaften der Seitenlängen von Parallelogrammen,
- unter Verwendung Semantik der Begriffsbezeichnung,
Lösung von Aufgabe 2.03 SoSe 2013 S
Aufgabe 2.04 SoSe 2013
Sie haben einen Klassensatz Heidelberger Winkelkreuze (Heidelberger_Winkelkreuz). Mit dem Heidelberger Winkelkreuz lassen Sie Ihre Schüler nur Parallelogramme spannen. Danach sollen eine Regel entwickeln, welche Stifte auf den Schenkeln des Kreuzes auszuwählen sind, damit ein Parallelogramm gespannt wird.
- Wie könnte diese Regel formuliert sein?
- Formulieren Sie eine Definition des Begriffs Parallelogramm, der sich unmittelbar aus dieser Regel ergibt.
Lösung von Aufgabe 2.04 SoSe 2013 S
